Es gibt Punkte des Querschnitts der Tunnelwand, deren Abstand zu \(M\) minimal ist. Bestimmen Sie die \(x\)-Koordinaten der Punkte \(P_{x}\), für die \(d(x)\) minimal ist, und geben Sie davon ausgehend diesen minimalen Abstand an.
(5 BE)
Lösung zu Teilaufgabe 1c
Extremwertaufgabe, Tangentensteigung, Normalensteigung
\[d(x) = \sqrt{0{,}04x^{4} - x^{2} + 25}\]
1. Lösungsansatz: Extremwertaufgabe
Mithilfe der aus Teilaufgabe 1b bekannten Funktion \(d\), welche den Abstand der Punkte \(P_{x}\) vom Ursprung \(M\) des Koordinatensystems beschreibt, bestimmt man die Extremstellen von \(d\) und damit auch den minimalen Abstand.
Lage der Extremstellen
Notwendige Bedingung für eine Extremstelle der Funktion \(d\):
\[d'(x) \overset{!}{=} 0\]
Este Ableitung \(d'\) bilden:
Die Ableitungsfunktion \(d'\) kann mithilfe der Ableitung einer Wurzelfunktion und einer Potenzfunktion sowie unter Berücksichtigung der Kettenregel, der Faktorregel und der Summenregel gebildet werden.
\[d(x) = \sqrt{0{,}04x^{4} - x^{2} + 25}\]
Ableitung einer Wurzelfunktion
\[f(x) = \sqrt{g(x)} \quad \Longrightarrow \quad f'(x) = \frac{g'(x)}{2\sqrt{g(x)}} \quad (g(x) \geq 0)\]
Kettenregel
\[f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\begin{align*} d'(x) &= \frac{4 \cdot 0{,}04x^{3} - 2x + 0}{2 \sqrt{0{,}04x^{4} - x^{2} + 25}} \\[0.8em] &= \frac{0{,}16x^{3} - 2x}{2 \sqrt{0{,}04x^{4} - x^{2} + 25}} \end{align*}\]
Als Alternative formuliert man den Funktionsterm \(d(x)\) in der Poteznschreibweise und leitet anschließend mithilfe der Ableitung einer Potenfunktion sowie unter Berücksichtigung der Kettenregel, der Faktorregel und der Summenregel ab.
\[\begin{align*}d(x) &= \sqrt{0{,}04x^{4} - x^{2} + 25} & &| \; \sqrt[n]{a} = a^{\frac{1}{n}} \\[0.8em] &= \left(0{,}04x^{4} - x^{2} + 25 \right)^{\frac{1}{2}} \end{align*}\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Kettenregel
\[f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\begin{align*} d'(x) &= \frac{1}{2} \cdot \left( 0{,}04x^{4} - x^{2} + 25 \right)^{-\frac{1}{2}} \cdot \left( 4 \cdot 0{,}04x^{3} - 2x + 0 \right) \\[0.8em] &= \frac{1}{2} \cdot \left( 0{,}04x^{4} - x^{2} + 25 \right)^{-\frac{1}{2}} \cdot \left( 0{,}16x^{3} - 2x \right) & &| \; a^{\frac{1}{n}} = \sqrt[n]{a}; \; a^{-n} = \frac{1}{a^{n}} \\[0.8em] &= \frac{0{,}16x^{3} - 2x}{2 \sqrt{0{,}04x^{4} - x^{2} + 25}} \end{align*}\]
Nullstellen von \(d'\) bestimmen:
\[d'(x) = \frac{0{,}16x^{3} - 2x}{2 \sqrt{0{,}04x^{4} - x^{2} + 25}}\]
\[\begin{align*} d'(x) = 0 \quad \Longrightarrow \quad 0{,}16x^{3} - 2x &= 0 \\[0.8em] x \cdot \left( 0{,}16x^{2} - 2 \right) &= 0 \end{align*}\]
\[\begin{align*}\Longrightarrow \quad x_{1} = 0 \enspace \vee \enspace 0{,}16x^{2} - 2 &= 0 & &| - 2 \\[0.8em] 0{,}16x^{2} &= 2 & &| : 0{,}16 \\[0.8em] x^{2} &= 12{,}5 & &| \; \sqrt{\enspace} \\[0.8em] x_{2,3} &= \pm \frac{5\sqrt{2}}{2} \end{align*}\]
Nachweis der Art der Extremstellen
1. Möglichkeit: Berücksichtigung des Ergebnisses aus Teilaufgabe 1a
Aus Teilaufgabe 1a ist bekannt, dass der Graph der Funktion \(p\) (Parabel) an der Stelle \(x = 0\) einen Hochpunkt \(HoP(0|5)\) (Scheitelpunkt \(S(0|5)\)) hat und somit Bedingung II erfüllt ist. Das bedeutet, dass der Abstand \(d(0) = 5\) maximal ist. Punkte \(P_{x}\), deren Abstand zu \(M\) minimal ist, sind folglich an den Stellen \(x_{2,3} = \pm \frac{5\sqrt{2}}{2}\) zu erwarten.
2. Möglichkeit: Monotoniekriterium bzw. Monotonietabelle
Anwendung der Differetialrechnung:
Monotoniekriterium
\(f'(x) < 0\) im Intervall \( I \enspace \Rightarrow \enspace G_{f}\) fällt streng monoton in \(I\)
\(f'(x) > 0\) im Intervall \( I \enspace \Rightarrow \enspace G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\[d'(x) = \frac{0{,}16x^{3} - 2x}{2 \sqrt{0{,}04x^{4} - x^{2} + 25}}\]
Mithilfe der Nullstellen \(x_{1} = 0\) sowie \(x_{2,3} = \pm \frac{5\sqrt{2}}{2}\) von \(d'\) lässt sich der Term des Zählers von \(d'\) faktorisieren (Linearfaktorzerlegung). Der Vorzeichenwechsel von \(d'\) ist dann besser zu erkennen.
\[\begin{align*}d'(x) &= \frac{0{,}16x^{3} - 2x}{2 \sqrt{0{,}04x^{4} - x^{2} + 25}} \\[0.8em] &= \frac{0{,}16x \cdot \left(x^{2} - 12{,}5\right)}{2 \sqrt{0{,}04x^{4} - x^{2} + 25}} \\[0.8em] &= \frac{0{,}16x \cdot \left(x - \frac{5\sqrt{2}}{2}\right) \cdot \left(x + \frac{5\sqrt{2}}{2} \right)}{\underbrace{2 \sqrt{0{,}04x^{4} - x^{2} + 25}}_{\large > \, 0}} \end{align*}\]
Der Term des Zählers der Ableitungsfunktion \(d'\) bestimmt den Vorzeichenwechsel von \(d'\).
\[\left. \begin{align*} &d'(x) < 0 \enspace \text{für} \enspace x < \textstyle -\frac{5\sqrt{5}}{2} \\[0.8em] &d'\left(\textstyle -\frac{5\sqrt{2}}{2} \right) = 0 \\[0.8em] &d'(x) > 0 \enspace \text{für} \; \textstyle -\frac{5\sqrt{5}}{2} < x < 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{minimaler Abstand} \; d\left(\textstyle -\frac{5\sqrt{2}}{2} \right)\]
\[\left. \begin{align*} &d'(x) > 0 \enspace \text{für} \; \textstyle -\frac{5\sqrt{5}}{2} < x < 0 \\[0.8em] &d'(0) = 0 \\[0.8em] &d'(x) < 0 \enspace \text{für} \enspace 0 < x < \textstyle \frac{5\sqrt{5}}{2} \end{align*} \right\} \enspace \Rightarrow \enspace \text{maximaler Abstand} \; d(0)\]
\[\left. \begin{align*} &d'(x) < 0 \enspace \text{für} \enspace 0 < x < \textstyle \frac{5\sqrt{5}}{2} \\[0.8em] &d'\left( \textstyle \frac{5\sqrt{2}}{2} \right) = 0 \\[0.8em] &d'(x) > 0 \enspace \text{für} \enspace x > \textstyle \frac{5\sqrt{5}}{2} \end{align*} \right\} \enspace \Rightarrow \enspace \text{minimaler Abstand} \; d\left( \textstyle \frac{5\sqrt{2}}{2} \right)\]
Veranschaulichung mithilfe einer Monotonietabelle:
| \(x\) | \(x < -\frac{5\sqrt{2}}{2}\) | \(-\frac{5\sqrt{2}}{2}\) | \(-\frac{5\sqrt{2}}{2} < x < 0\) |
| \(d'(x)\) | \(-\) | \(0\) | \(+\) |
| \(G_{d}\) | \(\searrow\) | \(TiP\) | \(\nearrow\) |
| \(d(x)\) | minimal |
| \(x\) | \(-\frac{5\sqrt{2}}{2} < x < 0\) | \(0\) | \(0 < x < \frac{5\sqrt{2}}{2}\) |
| \(d'(x)\) | \(+\) | \(0\) | \(-\) |
| \(G_{d}\) | \(\nearrow\) | \(HoP\) | \(\searrow\) |
| \(d(x)\) | maximal |
| \(x\) | \(0 < x < \frac{5\sqrt{2}}{2}\) | \(\frac{5\sqrt{2}}{2}\) | \(x > \frac{5\sqrt{2}}{2}\) |
| \(d'(x)\) | \(-\) | \(0\) | \(+\) |
| \(G_{d}\) | \(\searrow\) | \(TiP\) | \(\nearrow\) |
| \(d(x)\) | minimal |
Anmerkung: Auf den Nachweis der Art der Extremstellen mithilfe der zweiten Ableitung \(d''\) wird an dieser Stelle verzichtet, da dieser aufgrund des höheren Aufwandes keine sinnvolle Alternative darstellt.
Minimaler Abstand
Aufgrund der Achsensymmetrie der Parabel der Funktion \(p\) zur \(y\)-Achse ergibt sich:
\[\begin{align*}d\left(-\frac{5\sqrt{2}}{2}\right) = d\left(\frac{5\sqrt{2}}{2}\right) &= \sqrt{0{,}04 \cdot \left( \frac{5\sqrt{2}}{2} \right)^{4} - \left( \frac{5\sqrt{2}}{2} \right)^{2} + 25} \\[0.8em] &= \frac{5\sqrt{3}}{2} \\[0.8em] &\approx 4{,}33\end{align*}\]
Betrachtung möglicher Randminima:
Differenzierbarkeit
Existiert für eine Funktion \(f\) an der Stelle \(x_0\) der Differentialquotient
\(\displaystyle f'(x_0) \, = \, \lim \limits_{x\,\to\,x_0} \frac{f(x) - f(x_0)}{x - x_0} \, = \, \lim \limits_{h\,\to\,0} \frac{f(x_0 + h) - f(x_0)}{h}\,\),
heißt die Funktion \(f\) differenzierbar an der Stelle \(\bf{x_0}\).
Der Differentialquotient existiert, wenn der linksseitige Grenzwert des Differentialquotienten (\(\underset{\textcolor{#cc071e}{x\,<\,x_0}}{x\,\to\,x_0}\) bzw. \(\underset{\textcolor{#cc071e}{h\,<\,0}}{h\,\to\,0}\)) und der rechtsseitige Grenzwert des Differentialquotienten (\(\underset{\textcolor{#0087c1}{x\,>\,0}}{x\,\to\,x_0}\) bzw. \(\underset{\textcolor{#0087c1}{h\,>\,0}}{h\,\to\,0}\)) übereinstimmen.
Mit dem Definitionsbereich \(D_{p} = [-5;5]\) der Funktion \(p\) ist auch die Funktion \(d\) für \(x \in [-5;5]\) definiert. Die Definitionsränder \(x = -5\) und \(x = 5\) werden bei der Berechnung der Extremstellen nicht erfasst, da die Funktion \(d\) dort nicht differenzierbar ist.
Die Ableitung \(d'(-5)\) bzw. \(d'(5)\), das heißt, der Differentialquotient \(\displaystyle \lim \limits_{x \, \to \, -5} \frac{d(x) - d(-5)}{x + 5}\) bzw. \(\displaystyle \lim \limits_{x \, \to \, 5} \frac{d(x) - d(5)}{x - 5}\) existiert nicht.
Wie aus Teilaufgabe 1a bekannt ist, ist Bedingung I mit b = 10 m erfüllt. Somit ist der Abstand \(d(-5) = 5\) bzw. \(d(5) = 5\) maximal und es existieren keine Randminima. Dies lässt sich ebenfalls rechnerisch bestätigen:
\[d(x) = \sqrt{0{,}04x^{4} - x^{2} + 25}; \; D_{d} = [-5;5]\]
\[d(-5) = \sqrt{0{,}04 \cdot (-5)^{4} - (-5)^{2} + 25} = \sqrt{0{,}04 \cdot 625} = \sqrt{25} = 5\]
\[d(5) = \sqrt{0{,}04 \cdot 5^{4} - 5^{2} + 25} = \sqrt{0{,}04 \cdot 625} = \sqrt{25} = 5\]
\(\Longrightarrow \quad\)An den Stellen \(x = -\frac{5\sqrt{2}}{2}\) und \(x = \frac{5\sqrt{2}}{2}\) ist der Abstand der Punkte \(P_{x}\) des Querschnitts der Tunnelwand zu \(M\) mit ca. 4,33 m minimal.
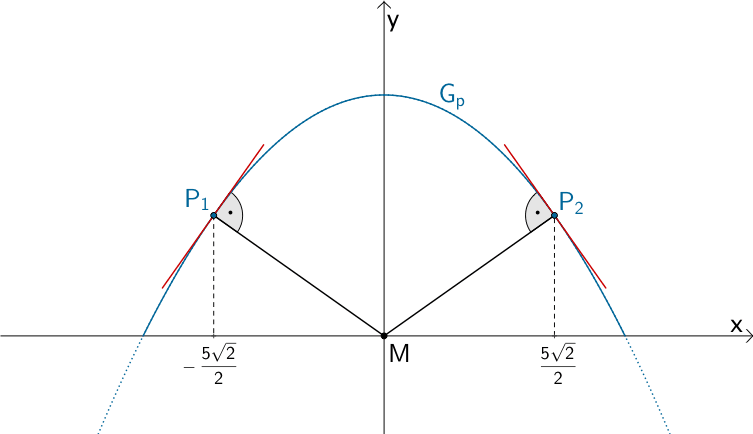
Punkte \(P_{1}, P_{2} \in G_{p}\), deren Abstand zum Ursprung des Koordinatensystems \(M\) minimal ist. Die Strecke \([MP_{1}]\) bzw. \([MP_{2}]\) ist senkrecht zur Tangente an \(G_{p}\) an der Stelle \(x_{1} = -\frac{5\sqrt{2}}{2}\) bzw. \(x_{2} = \frac{5\sqrt{2}}{2}\).
2. Lösungsansatz: Normale durch \(M\) an \(G_{p}\) in \(P_{x}\)
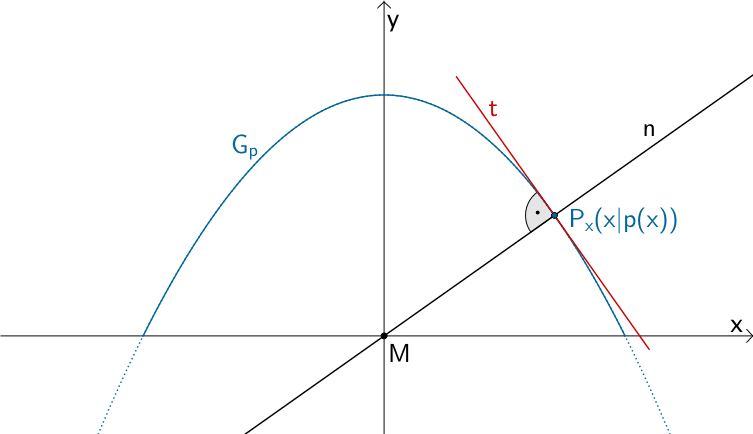
Ein Graphenpunkt \(P_{x}(x|p(x))\) der Parabel der Funktion \(p\), dessen Abstand zum Ursprung des Koordinatensystems \(M\) minimal ist, ist Lotfußpunkt des Lotes des Punktes \(M\) auf die Tangente \(t\) an \(G_{p}\) im Punkt \(P_{x}\). Ein Punkt \(P_{x}\), dessen Abstand zu \(M\) minimal ist, ist folglich ein Schnittpunkt der Normalen \(n\) in \(P_{x}(x|p(x))\) durch \(M\) und der Parabel der Funktion \(p\).
Gleichung einer Normalen \(n\):
Für die Steigung \(m_{N}\) der Normalen \(n\) in einem Graphenpunkt \(P_{x}(x|p(x))\) gilt:
Anwendung der Differetialrechnung:
Tangentensteigung und Normalensteigung
Tangentensteigung: \(m_{T} = f'(x_0)\)
Normalensteigung: \(m_{N} = -\dfrac{1}{f'(x_0)}\)
(vgl. Merkhilfe)
\[m_{N} = - \frac{1}{p'(x)}\]
Die Normale \(n\) durch den Punkt \(M(0|0)\) ist eine Ursprungsgerade.
\[\Longrightarrow \quad n \colon y = -\frac{1}{p'(x)} \cdot x\]
Schnittstellen der Parabel der Funktion \(p\) mit der Normalen \(n\) berechnen:
Für die Berechnung der Schnittstellen werden die Funktionsterme der Funktion \(p\) und der Normalen \(n\) gleichgesetzt.
\[p(x) = -0{,}2x^{2} + 5; \; D_{p} = [-5;5]\]
\(p'(x) = -0{,}4x\) (vgl. Teilaufgabe 1a)
\[n(x) = -\frac{1}{p'(x)} \cdot x\]
\[\begin{align*} p(x) &= n(x) \\[0.8em] p(x) &= -\frac{1}{p'(x)} \cdot x \\[0.8em] -0{,}2x^{2} + 5 &= -\frac{1}{-0{,}4 \cdot \cancel{x}} \cdot \cancel{x} & &| \; x \neq 0 \\[0.8em] -0{,}2x^{2} + 5 &= 2{,}5 & &| - 5 \\[0.8em] -0{,}2x^{2} &= -2{,}5 & &| : (-0{,}2) \\[0.8em] x^{2} &= 12{,}5 & &| \; \sqrt{\enspace} \\[0.8em] x_{1,2} &= \pm \frac{5\sqrt{2}}{2} \end{align*}\]
Bei der Auflösung der Gleichung wurde der Fall \(x = 0\) ausgeschlossen (Kürzen). Er muss gesondert betrachtet werden.
Aus Teilaufgabe 1a ist bekannt, dass der Graph der Funktion \(p\) (Parabel) an der Stelle \(x = 0\) einen Hochpunkt \(HoP(0|5)\) (Scheitelpunkt \(S(0|5)\)) hat und somit Bedingung II erfüllt ist. Das bedeutet, dass der Abstand \(d(0) = 5\) maximal ist. Punkte \(P_{x}\), deren Abstand zu \(M\) minimal ist, sind folglich an den Stellen \(x_{1,2} = \pm \frac{5\sqrt{2}}{2}\) zu erwarten.
Minimaler Abstand
Aufgrund der Achsensymmetrie der Parabel der Funktion \(p\) zur \(y\)-Achse ergibt sich:
\[\begin{align*}d\left(-\frac{5\sqrt{2}}{2}\right) = d\left(\frac{5\sqrt{2}}{2}\right) &= \sqrt{0{,}04 \cdot \left( \frac{5\sqrt{2}}{2} \right)^{4} - \left( \frac{5\sqrt{2}}{2} \right)^{2} + 25} \\[0.8em] &= \frac{5\sqrt{3}}{2} \\[0.8em] &\approx 4{,}33\end{align*}\]
Betrachtung der Definitionsränder von \(p\):
Differenzierbarkeit
Existiert für eine Funktion \(f\) an der Stelle \(x_0\) der Differentialquotient
\(\displaystyle f'(x_0) \, = \, \lim \limits_{x\,\to\,x_0} \frac{f(x) - f(x_0)}{x - x_0} \, = \, \lim \limits_{h\,\to\,0} \frac{f(x_0 + h) - f(x_0)}{h}\,\),
heißt die Funktion \(f\) differenzierbar an der Stelle \(\bf{x_0}\).
Der Differentialquotient existiert, wenn der linksseitige Grenzwert des Differentialquotienten (\(\underset{\textcolor{#cc071e}{x\,<\,x_0}}{x\,\to\,x_0}\) bzw. \(\underset{\textcolor{#cc071e}{h\,<\,0}}{h\,\to\,0}\)) und der rechtsseitige Grenzwert des Differentialquotienten (\(\underset{\textcolor{#0087c1}{x\,>\,0}}{x\,\to\,x_0}\) bzw. \(\underset{\textcolor{#0087c1}{h\,>\,0}}{h\,\to\,0}\)) übereinstimmen.
Die Definitionsränder \(x = -5\) und \(x = 5\) des Definitionsbereichs \(D_{p} = [-5;5]\) der Funktion \(p\) werden bei der Berechnung der Schnittstellen nicht erfasst, da die Funktion \(p\) dort nicht differenzierbar ist.
Die Ableitung \(p'(-5)\) bzw. \(p'(5)\), das heißt, der Differentialquotient \(\displaystyle \lim \limits_{x \, \to \, -5} \frac{p(x) - p(-5)}{x + 5}\) bzw. \(\displaystyle \lim \limits_{x \, \to \, 5} \frac{p(x) - p(5)}{x - 5}\), existiert nicht.
Da eine Parabel die \(x\)-Achse stets unter einem Winkel ungleich 90° schneidet (vgl. auch Teilaufgabe 1a: Spitzer Winkel, unter dem die linke Tunnelwand auf den Tunnelboden trifft), kann es in den Punkten \((-5|0)\) bzw. \((5|0)\) keine Normale durch \(M\) geben.
\(\Longrightarrow \quad\)An den Stellen \(x = -\frac{5\sqrt{2}}{2}\) und \(x = \frac{5\sqrt{2}}{2}\) ist der Abstand der Punkte \(P_{x}\) des Querschnitts der Tunnelwand zu \(M\) mit ca. 4,33 m minimal.
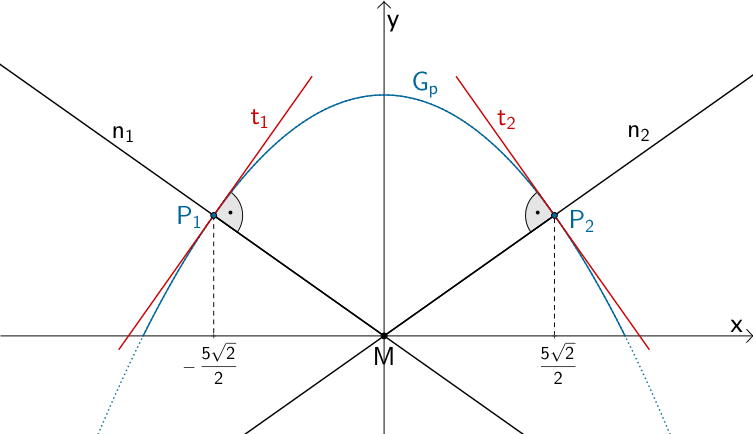
Punkte \(P_{1}, P_{2} \in G_{p}\), deren Abstand zum Ursprung des Koordinatensystems \(M\) minimal ist. Normale \(n_{1}\) in \(P_{1}\) durch \(M\) und Normale \(n_{2}\) in \(P_{2}\) durch \(M\).

