Es wird das Flächenstück zwischen \(G_{g}\) und der \(x\)-Achse im Bereich \(-\ln{3} \leq x \leq b\) mit \(b \in \mathbb R^{+}\) betrachtet. Bestimmen Sie den Wert von \(b\) so. dass die \(y\)-Achse dieses Flächenstück halbiert.
(6 BE)
Lösung zu Teilaufgabe 2d
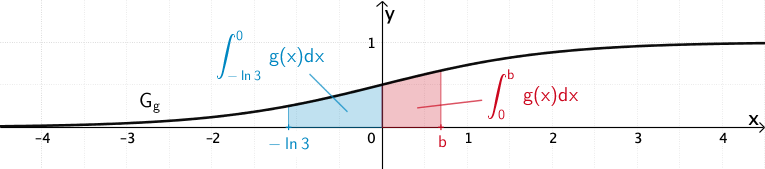
Planskizze (optional)
Das bestimmte Integral \(\displaystyle \int_{-\ln{3}}^{b}g(x)dx = \textcolor{#0087c1}{\int_{-\ln{3}}^{0}g(x)dx} + \textcolor{#cc071e}{\int_{0}^{b}g(x)dx}\) errechnet die Maßzahl des Inhalts der Fläche, die \(G_{g}\) im Bereich \(-\ln{3} \leq x \leq b\) mit \(b \in \mathbb R^{+}\) mit der \(x\)-Achse einschließt.
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
Die \(y\)-Achse halbiert die Fläche, wenn \(\displaystyle \textcolor{#0087c1}{\int_{-\ln{3}}^{0}g(x)dx} = \textcolor{#cc071e}{\int_{0}^{b}g(x)dx}\) gilt.
Wichtige unbestimmte Integrale (\(C \in \mathbb R\), vgl. Merkhilfe)
\[\int x^{r} dx = \frac{x^{r + 1}}{r + 1} + C \quad (r \neq - 1)\]
\[\int \frac{1}{x}\,dx = \ln{\vert x \vert} + C\]
\[\int \sin{x} \, dx = -\cos{x} + C\]
\[\int \cos{x} \, dx = \sin{x} + C\]
\[\int e^{x} dx = e^{x} + C\]
\[\int \ln{x}\, dx = -x + x \cdot \ln{x} + C\]
\[\int \frac{f'(x)}{f(x)} dx = \ln{\vert f(x) \vert} + C\]
\[\int f'(x) \cdot e^{f(x)} dx = e^{f(x)} + C\]
\(\displaystyle \int f(ax + b) \, dx = \frac{1}{a} \cdot F(ax + b) + C\), wobei \(F\) eine Stammfunktion von \(f\) ist.
Es gilt die Faktorregel und die Summenregel:
\(\displaystyle \int c \cdot f(x)\,dx = c \cdot \int f(x)\,dx\) mit \(c \in \mathbb R\)
\( \displaystyle \int \left[f(x) \pm g(x) \right] dx = \int f(x)\,dx \pm \int g(x)\,dx\)
\[\begin{align*} \textcolor{#0087c1}{\int_{-\ln{3}}^{0}g(x)dx} &= \textcolor{#cc071e}{\int_{0}^{b}g(x)dx} \\[0.8em] \int_{-\ln{3}}^{0}\frac{\textcolor{#e9b509}{e^{x}}}{\textcolor{#e9b509}{e^{x} + 1}}dx &= \int_{0}^{b}\frac{\textcolor{#e9b509}{e^{x}}}{\textcolor{#e9b509}{e^{x} + 1}}dx &&| \; \int \frac{\textcolor{#e9b509}{f'(x)}}{\textcolor{#e9b509}{f(x)}}dx = \textcolor{#e9b509}{\ln{\vert f(x) \vert} + C}\\&&&\enspace \; \text{(vgl. Merkhilfe)} \\[0.8em] \big[ \textcolor{#e9b509}{\underbrace{\ln{\vert e^{x} + 1 \vert}}_{\text{Stammfunktion}}} \big]_{\textcolor{#89ba17}{-\ln{3}}}^{\textcolor{#89ba17}{0}} &= \big[ \textcolor{#e9b509}{\underbrace{\ln{\vert e^{x} + 1 \vert}}_{\text{Stammfunktion}}} \big]_{\textcolor{#89ba17}{0}}^{\textcolor{#89ba17}{b}} \\[0.8em] \ln{\vert e^{\textcolor{#89ba17}{0}} + 1 \vert} - \ln{\vert e^{\textcolor{#89ba17}{-\ln{3}}} + 1 \vert} &= \ln{\vert e^{\textcolor{#89ba17}{b}} + 1 \vert} - \ln{\vert e^{\textcolor{#89ba17}{0}} + 1 \vert} &&| \; e^{0} = 1 \\[0.8em] \ln{2} - \ln{\vert e^{-\ln{3}} + 1 \vert} &= \ln{\vert e^{b} + 1 \vert} - \ln{2} &&| + \ln{2} \\[0.8em] 2\ln{2} - \ln{\vert e^{\textcolor{#e9b509}{-\ln{3}}} + 1 \vert} &= \ln{\vert e^{b} + 1 \vert} &&| \; \textcolor{#e9b509}{\log_{a}{b^{r}} = r \cdot \log_{a}{b}}\\&&&\enspace\;\text{(vgl. Merkhilfe)} \\[0.8em] 2\ln{2} - \ln{\vert e^{\textcolor{#e9b509}{\ln{3^{-1}}}} + 1 \vert} &= \ln{\vert e^{b} + 1 \vert} \\[0.8em] 2\ln{2} - \ln{\vert \textcolor{#e9b509}{e^{\ln{\frac{1}{3}}}} + 1 \vert} &= \ln{\vert e^{b} + 1 \vert}&&|\;\textcolor{#e9b509}{e^{\ln{b}} = b}\;(\text{allg.:}\;a^{\log_{a}{b}} = b) \\[0.8em] 2\ln{2} - \ln{\left| \textcolor{#e9b509}{\frac{1}{3}} + 1 \right|} &= \ln{\vert e^{b} + 1 \vert} \\[0.8em] \textcolor{#e9b509}{2\ln{2}} - \ln{\frac{4}{3}} &= \ln{\vert e^{b} + 1 \vert} &&|\; \textcolor{#e9b509}{\log_{a}{b^{r}} = r \cdot \log_{a}{b}}\\&&&\enspace\;\text{(vgl. Merkhilfe)} \\[0.8em] \textcolor{#e9b509}{\ln{2^{2}}} - \ln{\frac{4}{3}} &= \ln{\vert e^{b} + 1 \vert} \\[0.8em] \textcolor{#e9b509}{\ln{4} - \ln{\frac{4}{3}}} &= \ln{\vert e^{b} + 1 \vert}&&|\;\textcolor{#e9b509}{\log_{a}{\frac{b}{c}} = \log_{a}{b} - \log_{a}{c}}\\&&&\enspace\;\text{(vgl. Merkhilfe)} \\[0.8em] \textcolor{#e9b509}{\ln{\frac{4}{\frac{4}{3}}}} &= \ln{\vert e^{b} + 1 \vert} \\[0.8em] \ln{3} &= \ln{\vert \underbrace{e^{b} + 1}_{>\,0} \vert} &&|\;e^{(\dots)}\;\text{(zur Basis}\;e\;\text{potenzieren)} \\[0.8em] \textcolor{#e9b509}{e^{\ln{3}}} &= \textcolor{#e9b509}{e^{\ln{(e^{b} + 1)}}}&&|\;\textcolor{#e9b509}{e^{\ln{b}} = b}\;(\text{allg.:}\;a^{\log_{a}{b}} = b) \\[0.8em] \textcolor{#e9b509}{3} &= \textcolor{#e9b509}{e^{b} + 1} &&| - 1 \\[0.8em] 2 &= e^{b} &&| \; \ln\;\text{(Logarithmieren)}\\[0.8em] \ln{2} &= \textcolor{#e9b509}{\ln{e^{b}}} &&|\;\textcolor{#e9b509}{\log_{a}{b^{r}} = r \cdot \log_{a}{b}}\\&&&\enspace\;\text{(vgl. Merkhilfe)}\\[0.8em] \ln{2} &= \textcolor{#e9b509}{b \cdot \ln{e}}&&|\;\textcolor{#e9b509}{\ln{e} = 1}\;(\text{allg.:}\;\log_{a}{a} = 1) \\[0.8em] \ln{2} &= b \end{align*}\]

