Bestimmen Sie die Wahrscheinlichkeit \(P_{\overline{V}}(R)\).
(3 BE)
Teilaufgabe 3b
Lösung zu Teilaufgabe 3b
Mithilfe des Baumdiagramms aus Teilaufgabe 3a ergibt sich:
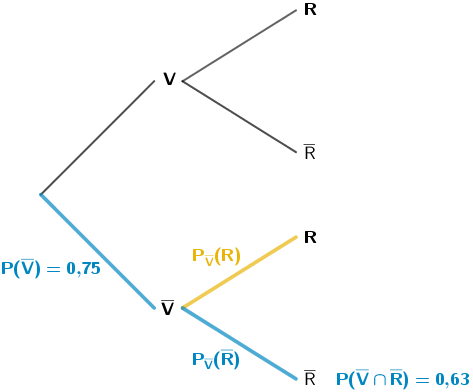
Baumdiagramm mit den Eintragungen der relevanten Wahrscheinlichkeiten (vgl. Teilaufgabe 3a)
\[\begin{align*}\textcolor{#e9b509}{P_{\overline{V}}(R)} &= 1 - \textcolor{#0087c1}{P_{\overline{V}}(\overline{R})} \\[0.8em] &= 1 - \frac{\textcolor{#0087c1}{P(\overline{V}\cap\overline{R})}}{\textcolor{#0087c1}{P(\overline{V})}} \\[0.8em] &= 1 - \frac{\textcolor{#0087c1}{0{}63}}{\textcolor{#0087c1}{0{,}75}} \\[0.8em] &= \textcolor{#e9b509}{0{,}16}\end{align*}\]
Oder mithilfe der Vierfeldertafel aus Teilaufgabe 3a:
| \(V\) | \(\overline{V}\) | ||
| \(R\) | \(0{,}105\) | \(0{,}12\) | \(\) |
| \(\overline{R}\) | \(0{,}145\) | \(\textcolor{#0087c1}{0{,}63}\) | \(0{,}775\) |
| \(\textcolor{#0087c1}{0{,}25}\) | \(\textcolor{#0087c1}{0{,}75}\) | \(1\) |
\[P(\overline{V}\cap R) = \textcolor{#0087c1}{P(\overline{V})} - \textcolor{#0087c1}{P(\overline{V}\cap \overline{R})} = \textcolor{#0087c1}{0{,}75} - \textcolor{#0087c1}{0{,}63} = 0{,}12\]
\[P_{\overline{V}}(R) = \frac{P(\overline{V}\cap R)}{\textcolor{#0087c1}{P(\overline{V})}} = \frac{0{,}12}{\textcolor{#0087c1}{0{,}75}} = 0{,}16\]
