Eine Funktion \(f\) mit \(f(x) = ax^{2} + bx + c\) und \(a,b,c \in \mathbb R, a \neq 0\) heißt quadratische Funktion. Quadratische Funktionen sind ganzrationale Funktionen 2. Grades (vgl. 1.1.3 ).
Definitionsmenge: \(D_{f} = \mathbb R\)
Funktionsgraph einer quadratischen Funktion
Der Funktionsgraph einer Quadratischen Funktion ist eine Parabel. Der Graph der Funktion \(f(x) = ax^{2}\) mit \(a = 1\) und Scheitelpunkt \(S(0|0)\) heißt Normalparabel. Der Koeffizient \(a\) bestimmt die Öffnung der Parabel und wird daher auch als Öffnungsfaktor bezeichnet. Für \(\vert a \vert > 1\) ist die Parabel enger, für \(\vert a \vert < 1\) ist die Parabel weiter als die Normalparabel.
\(a > 0\): Die Parabel ist nach oben geöffnet. Ihr Scheitelpunkt \(S\) ist zugleich Tiefpunkt.
\(a < 0\): Die Parabel ist nach unten geöffnet. Ihr Scheitelpunkt \(S\) ist zugleich Hochpunkt.
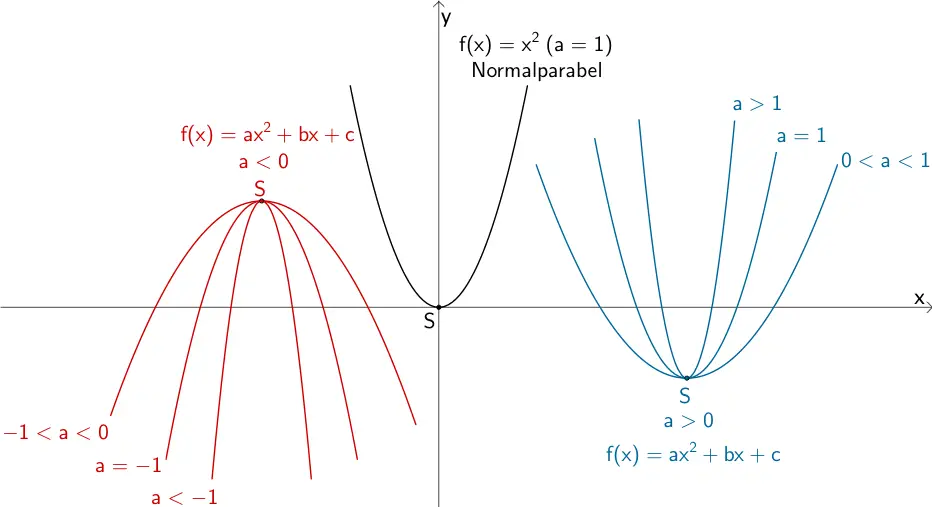
Parabeln von quadratischen Funktionen für verschiedene Öffnungsfaktoren \(a\)
Symmetrieverhalten
Jeder Graph quadratischen Funktion besitzt eine Symmetrieachse, welche parallel zur \(y\)-Achse durch den Scheitelpunkt \(S\) verläuft. Der Graph einer quadratischen Funktion mit \(f(x) = ax^{2} + c\) ist achsensymmetrisch zur \(y\)-Achse.
Scheitelpunktform einer quadratischen Funktion
Eine quadratische Funktion \(f\) mit \(f(x) = ax^{2} + bx + c\) kann durch quadratischen Ergänzung in die Scheitelpunktform umgewandelt werden. Aus der Scheitelpunktform lassen sich die Scheitpunktkoordinaten direkt entnehmen.
Scheitelpunktform
\[f(x) = a(x - d)^{2} + e\]
Scheitelpunkt \(S(d|e)\) mit \(d = -\dfrac{b}{2a}\) und \(e = c - \dfrac{b^{2}}{4a}\).
Nullstellen einer quadratischen Funktion
Die Lage des Scheitelpunkts \(S\) bzgl. der \(x\)-Achse und der Öffnungsfaktor \(a\) bestimmen die Anzahl der Nullstellen einer quadratischen Funktion.
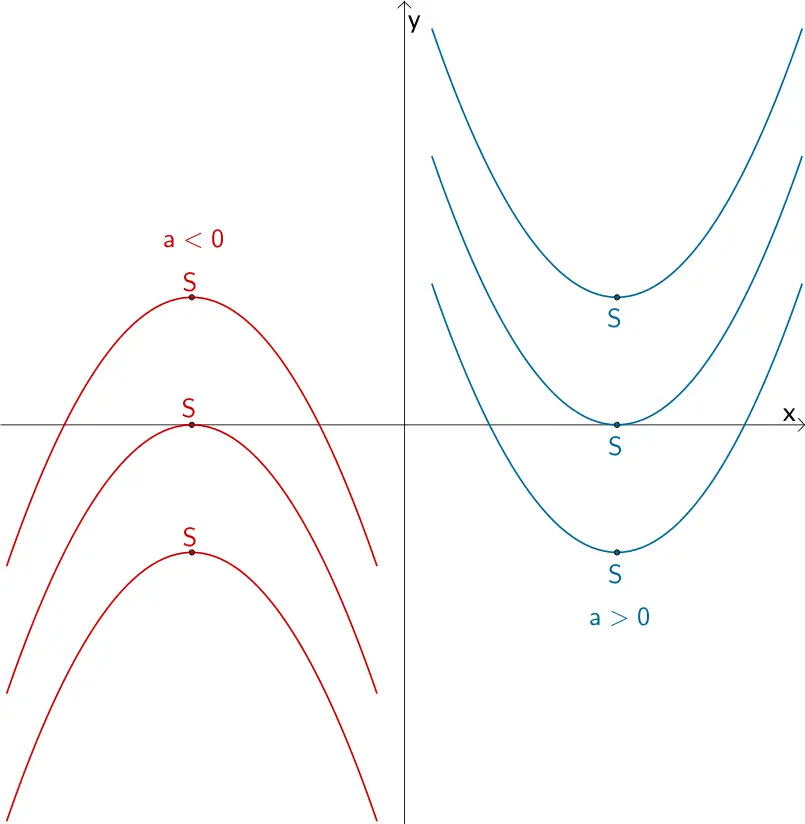
Eine quadratische Funktion besitzt abhängig von der Lage des Scheitelpunkts \(S\) der Parabel und dem Vorzeichen des Öffnungsfaktors \(a\) keine, eine oder zwei Nullstellen.
Um die Nullstellen einer quadratischen Funktion zu berechnen, ist die quadratische Gleichung \(ax^{2} + bx + c = 0\) zu lösen.
Lösungsformel für quadratische Gleichungen („Mitternachtsformel")
\[\begin{align*}x_{1,2} &= \frac{-b \pm \sqrt{D}}{2a}\,; \quad D \geq 0 \\[0.8em] \text{bzw.} \\[0.8em] x_{1,2} &= \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a}\,; \quad b^{2} \geq 4ac \end{align*}\]
Der Wert der Diskriminate \(D = b^{2} - 4ac\) entscheidet über die Anzahl der Lösungen einer quadratischen Gleichung und somit über die Anzahl der Nullstellen einer quadratischen Funktion.
\(D < 0\): keine Lösung bzw. keine Nullstelle
\(D = 0\): genau eine Lösung bzw. genau eine (doppelte) Nullstelle
\(D > 0\): zwei verschiedene Lösungen bzw. zwei verschiedene Nullstellen
Spezialfälle:
Nachfolgend genannte einfache Fälle lassen sich auch ohne die Lösungsformel für quadratische Gleichungen lösen.
\[ax^{2} + bx = 0 \enspace \Longleftrightarrow \enspace x \cdot (ax + b) \quad \Longrightarrow \quad x_{1} = 0;\; x_{2} = -\frac{b}{a} \enspace (a \neq 0)\]
\[ax^{2} + c = 0 \enspace \Longleftrightarrow \enspace x^{2} = -\frac{c}{a} \quad \Longleftrightarrow \quad x_{1,2} = \pm \sqrt{-\frac{c}{a}} \enspace (-\frac{c}{a} \geq 0)\]
Produktform und Linearfaktoren einer quadratischen Funktion
In Anwendungen ist es häufig vorteilhaft, den Term einer quadratischen Funktion als Produkt ihrer Linearfaktoren zu beschreiben. Existieren für die quadratische Gleichung \(ax^{2} + bx + c\) zwei Lösungen \(x_{1}\) und \(x_{2}\) (Parabel besitzt zwei Nullstellen), bezeichnet \(x - x_{1}\) und \(x - x_{2}\) zwei Linearfaktoren, mit denen sich die quadratische Funktion in der Produktform angeben lässt.
Produktform
\[f(x) = ax^{2} + bx + c = a(x - x_{1})(x - x_{2})\]
\(x_{1}, x_{2}\): Nullstellen von \(f\)
Besitzt eine quadratische Funktion nur eine (doppelte) Nullstelle \(x_{1} = x_{2}\), formuliert die Produktform einer quadratischen Funktion einen Sonderfall der Scheitelpunktform.
\[\begin{align*}f(x) &= ax^{2} + bx + c \\[0.8em] &= a(x - x_{1})(x - x_{1}) \\[0.8em] &= a(x - x_{1})^{2} \end{align*}\]
Scheitelpunkt: \(S(x_{1}|0)\)
Quadratische Ungleichungen
Das Lösen einer quadratischen Ungleichung der Form \(ax^{2} + bx + c < 0\) bzw. \(ax^{2} + bx + c > 0\) mit \(a \neq 0\) und \(b,c \in \mathbb R\) kann zum Beispiel im Falle einer Ableitungsfunktion der Form \(f' \colon x \mapsto (ax^{2} + bx + c) \cdot e^{kx}; \; k \in \mathbb R\) eine Alternative sein, um das Vorzeichen bzw. den Vorzeichenwechsel (VZW) von \(f'\) zu bestimmen (vgl. Abiturskript - 1.5.3 Monotonieverhalten, Extrem- und Terrassenpunkte).
\[f'(x) = \underbrace{(ax^{2} + bx + c)}_{\text{Bestimmt VZW von f'}} \cdot \underbrace{e^{kx}}_{>\,0}\]
\[ax^{2} + bx + c \textcolor{#cc071e}{<} 0 \enspace \Rightarrow \enspace f'(x) \textcolor{#cc071e}{<} 0\]
\[ax^{2} + bx + c \textcolor{#cc071e}{>} 0 \enspace \Rightarrow \enspace f'(x) \textcolor{#cc071e}{>} 0\]
Quadratische Ungleichungen halbgraphisch lösen
Beim halbgraphischen Lösen einer quadratischen Ungleichung wird die Parabel der quadratischen Funktion \(x \mapsto ax^{2} + bx + c\) mithilfe der Nullstellen und des Öffnungsfaktors \(a\) qualitativ skizziert.
Aus der Skizze lassen sich die Intervalle ablesen, in denen die Parabel unterhalb bzw. oberhalb der \(x\)-Achse verläuft, also die Intervalle für die \(ax^{2} + bx + c < 0\) bzw. \(ax^{2} + bx + c > 0\) gilt.
Beispiel: \(\dfrac{1}{2}x^{2} + \dfrac{1}{2}x - 3 < 0\)
Zunächst sind die Nullstellen der quadratischen Funktion \(x \mapsto \frac{1}{2}x^{2} + \frac{1}{2}x - 3\) mithilfe der Lösungsformel für quadratische Gleichungen zu bestimmen (vgl. Nullstellen einer quadratischen Funktion).
\[\begin{align*} \frac{1}{2}x^{2} + \frac{1}{2}x - 3 &= 0 &&| \cdot 2 \; (\text{optional, Vermeidung der Brüche}) \\[0.8em] x^{2} + x - 6 = 0 \end{align*}\]
\[x_{1,2} = \frac{-1 \pm \sqrt{1^{2} - 4 \cdot 1 \cdot (-6)}}{2 \cdot 1} = \frac{-1 \pm \sqrt{25}}{2} = \frac{-1 \pm 5}{2}\]
\[x_{1} = \frac{-1 - 5}{2} = \frac{-6}{2} = -3\]
\[x _{2} = \frac{-1 + 5}{2} = \frac{4}{2} = 2\]
Der Öffnungsfaktor \(\textcolor{#e9b509}{a = \frac{1}{2}}\) der quadratischen Funktion \(x \mapsto \textcolor{#e9b509}{\frac{1}{2}}x^{2} + \frac{1}{2}x - 3\) lässt erkennen, dass die zugehörige Parabel nach oben geöffnet ist (vgl. Funktionsgraph einer quadratischen Funktion). Zusammen mit den Nullstellen \(x_{1} = -3\) und \(x_{2} = 2\) ist der qualitative Verlauf der Parabel schnell skizziert.
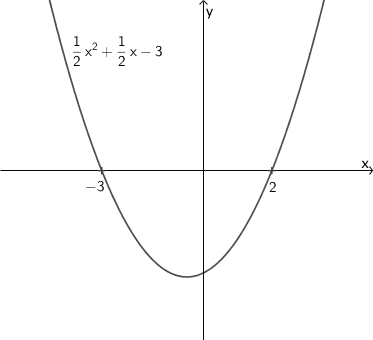
An der Skizze ist der Bereich abzulesen, in dem die Parabel unterhalb der \(x\)-Achse verläuft.
![Für x ∈ ]-3;2[ verläuft die Parabel von 0.5x² + 0.5x - 3 unterhalb der x-Achse](/images/stories/abi_check/analysis/Quadratische_Funktion_Ungleichung2.png)
Für \(x \in \; ]-3;2[\) verläuft die Parabel der quadratischen Funktion \(x \mapsto \frac{1}{2}x^{2} + \frac{1}{2}x - 3\) unterhalb der \(\textcolor{#cc071e}{x}\)-Achse. Also gilt in diesem Intervall: \(\textcolor{#cc071e}{\frac{1}{2}x^{2} + \frac{1}{2}x - 3 < 0}\).
Die Lösungsmenge der quadratischen Ungleichung \(\frac{1}{2}x^{2} + \frac{1}{2}x - 3 < 0\) lautet somit: \(L = \; ]-3;2[\).
Quadratische Ungleichungen durch Rechnung lösen
Quadratische Ungleichungen der Form \(ax^{2} + bx + c \textcolor{#cc071e}{< 0}\) bzw. \(ax^{2} + bx + c \textcolor{#cc071e}{> 0}\) mit \(a \neq 0\) und \(b,c \in \mathbb R\) lassen sich rechnerisch lösen, indem die quadratische Funktion \(x \mapsto ax^{2} + bx + c\) zunächst mithilfe der Nullstellen \(x _{1}\) und \(x_{2}\) in der Produktform \(a(x - x_{1})(x - x_{2})\) formuliert wird (vgl. Produktform und Linearfaktoren einer quadratischen Funktion).
Anschließend werden zwei Fälle unterschieden, für die das Produkt aus dem Öffnungsfaktor \(a\) und den beiden Linearfaktoren \((x - x_{1})\) und \((x - x_{2})\) kleiner bzw. größer als Null ist.
Beispiel einer Fallunterscheidung bei negativem Öffnungsfaktor \(\textcolor{#e9b509}{a < 0}\):
\[\begin{align*} ax^{2} + bx + c \; &\textcolor{#cc071e}{< 0}; \; \textcolor{#e9b509}{a < 0} \\[0.8em] \Leftrightarrow a(x - x_{1})(x - x_{2}) \; &\textcolor{#cc071e}{< 0}; \; \textcolor{#e9b509}{a < 0}\end{align*}\]
\[\begin{align*}\textsf{1. Fall:}\; \underbrace{\underbrace{a}_{\textcolor{#e9b509}{<\,0}} \cdot \underbrace{(x - x_{1})}_{<\,0} \cdot \underbrace{(x - x_{2})}_{<\,0}}_{\textcolor{#cc071e}{\large{<\,0}}} \; &\textcolor{#cc071e}{< 0} \\[0.8em] \textsf{2. Fall:}\; \underbrace{\underbrace{a}_{\textcolor{#e9b509}{<\,0}} \cdot \underbrace{(x - x_{1})}_{>\,0} \cdot \underbrace{(x - x_{2})}_{>\,0}}_{\textcolor{#cc071e}{\large{<\,0}}} \; &\textcolor{#cc071e}{< 0} \end{align*}\]
Es ergeben sich die nachfolgend tabellarisch zusammengefassten möglichen Fallunterscheiudungen:
| \(\textcolor{#e9b509}{a}(x - x_{1})(x - x_{2}) \textcolor{#cc071e}{< 0}\) | \(\textcolor{#e9b509}{a}(x - x_{1})(x - x_{2}) \textcolor{#cc071e}{> 0}\) | ||||
| \(\textcolor{#e9b509}{a < 0}\) | \(\textcolor{#e9b509}{a > 0}\) | \(\textcolor{#e9b509}{a < 0}\) | \(\textcolor{#e9b509}{a > 0}\) | ||
| 1. Fall | \((x - x_{1})\) | \(< 0\) | \(< 0\) | \(< 0\) | \(< 0\) |
| \((x - x_{2})\) | \(< 0\) | \(> 0\) | \(> 0\) | \(< 0\) | |
| 2. Fall | \((x - x_{1})\) | \(> 0\) | \(> 0\) | \(> 0\) | \(> 0\) |
| \((x - x_{2})\) | \(> 0\) | \(< 0\) | \(< 0\) | \(> 0\) | |
Sonderfälle:
Hat eine quadratische Funktion \(x \mapsto \textcolor{#e9b509}{a}x^{2} + bx + c\) keine Nullstelle, so gilt
- für \(\textcolor{#e9b509}{a < 0}\colon \enspace \textcolor{#e9b509}{a}x^{2} + bx + c \textcolor{#cc071e}{< 0}\) für alle \(x \in \mathbb R\) und
- für \(\textcolor{#e9b509}{a > 0}\colon \enspace \textcolor{#e9b509}{a}x^{2} + bx + c \textcolor{#cc071e}{> 0}\) für alle \(x \in \mathbb R\).
Hat eine quadratische Funktion \(x \mapsto \textcolor{#e9b509}{a}x^{2} + bx + c = 0\) genau eine Nullstelle \(x_{1}\), so gilt
- für \(\textcolor{#e9b509}{a < 0}\colon \enspace \textcolor{#e9b509}{a}x^{2} + bx + c \textcolor{#cc071e}{< 0}\) für alle \(x \in \mathbb R \backslash \{x_{1}\}\) und
- für \(\textcolor{#e9b509}{a > 0}\colon \enspace \textcolor{#e9b509}{a}x^{2} + bx + c \textcolor{#cc071e}{> 0}\) für alle \(x \in \mathbb R \backslash \{x_{1}\}\).
(vgl. Nullstellen einer quadratischen Funktion)
Beispiel: \(\dfrac{1}{2}x^{2} + \dfrac{1}{2}x - 3 < 0\)
Die Nullstellen der quadratischen Funktion \(x \mapsto \frac{1}{2}x^{2} + \frac{1}{2}x - 3\) sind \(x_{1} = -3\) und \(x_{2} = 2\) (vgl. Beispiel, halbgraphische Lösung). Damit lässt sich die quadratische Ungleichung in der Produktform darstellen.
\[\begin{align*} \textcolor{#e9b509}{\frac{1}{2}}x^{2} + \frac{1}{2}x - 3 \textcolor{#cc071e}{< 0} \\[0.8em] \textcolor{#e9b509}{\frac{1}{2}}(x + 3)(x - 2) \textcolor{#cc071e}{< 0}\end{align*}\]
Fallunterscheidung:
Mit \(\textcolor{#e9b509}{a > 0}\) ist die quadratische Ungleichung erfüllt, wenn die beiden Linearfaktoren \((x + 3)\) und \((x - 2)\) unterschiedliche Vorzeichen haben.
1. Fall:
\[\begin{align*}x + 3 & \; \textcolor{#cc071e}{< 0} && \wedge & x - 2 & \; \textcolor{#cc071e}{> 0} \\[0.8em] x &< - 3 && \wedge & x &> 2\end{align*}\]
Da sich die beiden Bereiche \(x < -3\) und \(x > 2\) nicht überschneiden, liefert der erste Fall keine Lösung.
2. Fall:
\[\begin{align*}x + 3 & \; \textcolor{#cc071e}{> 0} && \wedge & x - 2 & \; \textcolor{#cc071e}{< 0} \\[0.8em] x &> - 3 && \wedge & x &< 2\end{align*}\]
\[\Rightarrow \enspace - 3 < x < 2\]
Die Lösungsmenge der quadratischen Ungleichung \(\frac{1}{2}x^{2} + \frac{1}{2}x - 3 < 0\) lautet somit: \(L = \; ]-3;2[\).
Beispielaufgabe
Ermitteln Sie die Scheitelpunktform der Parabel \(p\colon y = 0{,}5x^{2} - 4x + 6\) und geben Sie die Koordinaten des Scheitelpunkts \(S\) an. Geben Sie die Anzahl der Nullstellen der Parabel \(p\) an und begründen Sie Ihre Antwort. Berechnen Sie ggf. anschließend die Nullstellen und geben Sie falls möglich die Parabelgleichung in der Produktform an.
\[p\colon y = 0{,}5x^{2} -4x + 6\]
Scheitelpunktform der Parabelgleichung:
Mithilfe der quadratischen Ergänzung lässt sich die Parabelgleichung in die Scheitelpunktform \(y = a(x - d)^{2} + e\) umwandeln. Dafür wird zunächst der Öffnungsfaktor \(0{,}5\) ausgeklammert, um anschließend den in der Klammer verbleibenden quadratischen Term geeignet so zu ergänzen, dass darauf die 1. bzw. 2. Binomische Formel angewendet werden kann.
\[\begin{align*} y &= 0{,}5x^{2} -4x + 6 & &| \; \text{Faktor}\; 0{,}5 \;\text{ausklammern} \\[0.8em] y &=0{,}5\left( x^{2} - 8x +12 \right) & &| \:\text{Quadratische Ergänzung:} + 4^{2} - 4^{2} \\[0.8em] y &= 0{,}5 \Big( \underbrace{x^{2} - 8x + 4^{2}}_{a^{2}\,-\,2ab\,+\,b^{2}\,=\,(a\,-\,b)^{2}} - 4^{2} + 12\Big) & &| \;\text{2. Binomische Formel anwenden} \\[0.8em] y &= 0{,}5 \left[ (x - 4)^{2} - 4^{2} + 12 \right] \\[0.8em] y &= 0{,}5 \left[ (x - 4)^{2} - 4 \right] \\[0.8em] y &= 0{,}5(x - 4)^{2} - 2 \end{align*}\]
Scheitelpunkt entnehmen: \(S(4|-2)\)
Nullstellen der Parabel \(p\):
Da der Scheitelpunkt der Parabel \(p\) unterhalb der \(x\)-Achse liegt und die Parabel mit dem Öffnungsfaktor \(0{,}5 > 0\) nach oben geöffnet ist, besitzt die Parabel \(p\) zwei Nullstellen.
\[p\colon y = 0{,}5x^{2} - 4x + 6\]
\[x_{1,2} = \frac{4 \pm \sqrt{(-4)^{2} - 4 \cdot 0{,}5 \cdot 6}}{2 \cdot 0{,}5} = 4 \pm \sqrt{4} = 4 \pm 2\]
\[x_{1} = 2\,;\enspace x_{2} = 6\]
Produktform (Linearfaktorzerlegung) der Parabelgleichung von \(p\):
\[y = 0{,}5x^{2} - 4x + 6 = 0{,}5(x - 2)(x - 6)\]
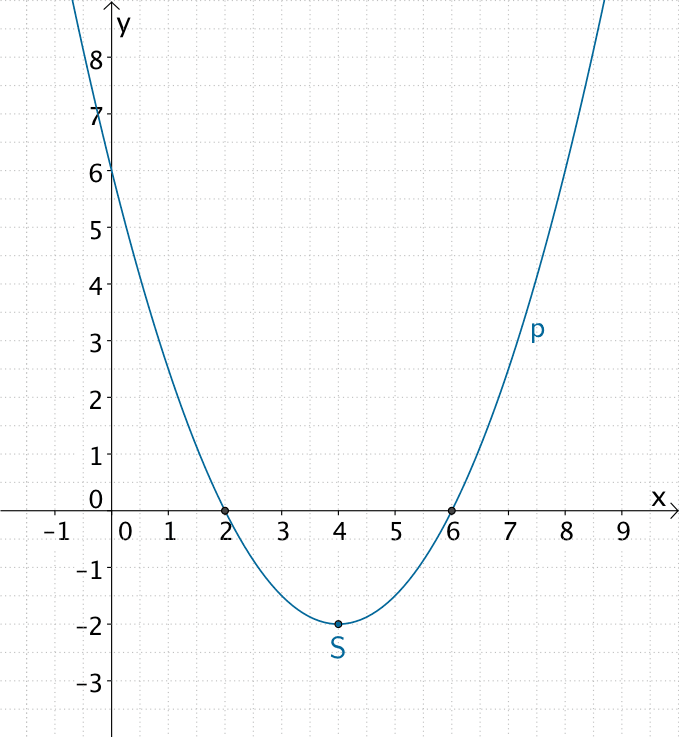
Parabel \(p\colon y = 0{,}5x^{2} - 4x + 6\) mit Scheitelpunkt \(S(4|-2)\) sowie den Nullstellen \(x_{1} = 2\) und \(x_{2} = 6\)

