- Details
- Kategorie: Analysis I - Teil 1
Geben Sie zu den Funktionstermen jeweils den maximalen Definitionsbereich sowie einen Term der Ableitungsfunktion an.
\[f(x)= \ln(x + 3)\]
(2 BE)
- Details
- Kategorie: Analysis I - Teil 1
Geben Sie zu den Funktionstermen jeweils den maximalen Definitionsbereich sowie einen Term der Ableitungsfunktion an.
\[g(x)= \frac{3}{x^2 - 1}\]
(3 BE)
- Details
- Kategorie: Analysis I - Teil 1
Geben Sie jeweils den Term einer in \(\mathbb R\) definierten Funktion an, die die angegebene Eigenschaft besitzt.
Der Graph der Funktion \(f\) hat den Hochpunkt \((0|5)\,\).
(2 BE)
- Details
- Kategorie: Analysis I - Teil 1
Die Funktion \(g\) ist an der Stelle \(x = 5\) nicht differenzierbar.
(2 BE)
- Details
- Kategorie: Analysis I - Teil 1
Gegeben ist die in \(\mathbb R\) definierte Funktion \(f \colon x \mapsto \sin(2x)\,\).
Geben Sie zwei benachbarte Nullstellen von \(f\) an.
(2 BE)
- Details
- Kategorie: Analysis I - Teil 1
Berechnen Sie den Wert des bestimmten Integrals \(\displaystyle \int_0^2 f(x)\,dx\,\).
Warum stimmt der Wert dieses Integrals nicht mit dem Inhalt der Fläche überein, die für \(0 \leq x \leq 2\) zwischen dem Graphen von \(f\) und der \(x\)-Achse liegt?
(5 BE)
- Details
- Kategorie: Analysis I - Teil 1
Abbildung 1 zeigt den Graphen \(G_f\) einer in \(]-\infty;5[\) definierten Funktion \(f\,\).
Skizzieren Sie in der Abbildung den Graphen der zugehörigen Ableitungsfunktion \(f'\,\). Berücksichtigen Sie dabei insbesondere einen Näherungswert für \(f'(0)\), die Nullstelle von \(f'\) und das Verhalten von \(f'\) für \(x \mapsto 5\,\).
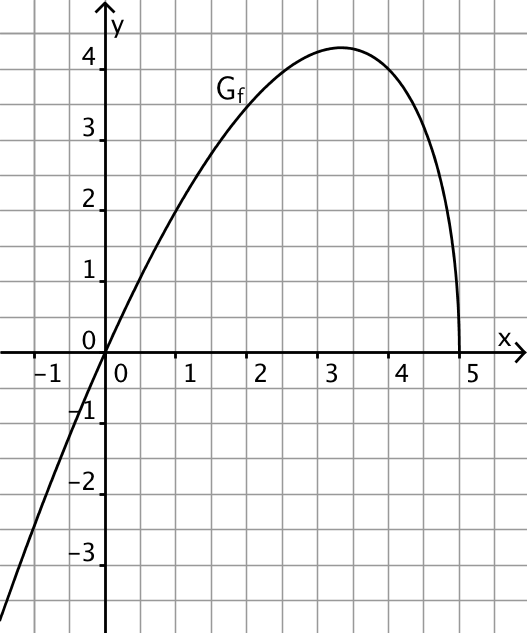 Abb. 1
Abb. 1
(4 BE)

