Von den im Baumdiagramm angegebenen Zahlenwerten soll nur der Wert \(\frac{\sf{1}}{\sf{10}}\) so geändert werden, dass die Ereignisse \(C\) und \(D\) unabhängig sind. Bestimmen Sie den geänderten Wert.
(2 BE)
Lösung zu Teilaufgabe 2c
1. Lösungsansatz: Gleiche bedingte Wahrscheinlichkeiten
Damit die Ereignisse \(C\) und \(D\) unabhängig sind, müssen die bedingten Wahrscheinlichkeiten \(P_{C}(D)\) und \(P_{\overline{C}}(D)\) an den zweiten Pfaden des Baumdiagramms denselben Wert haben.
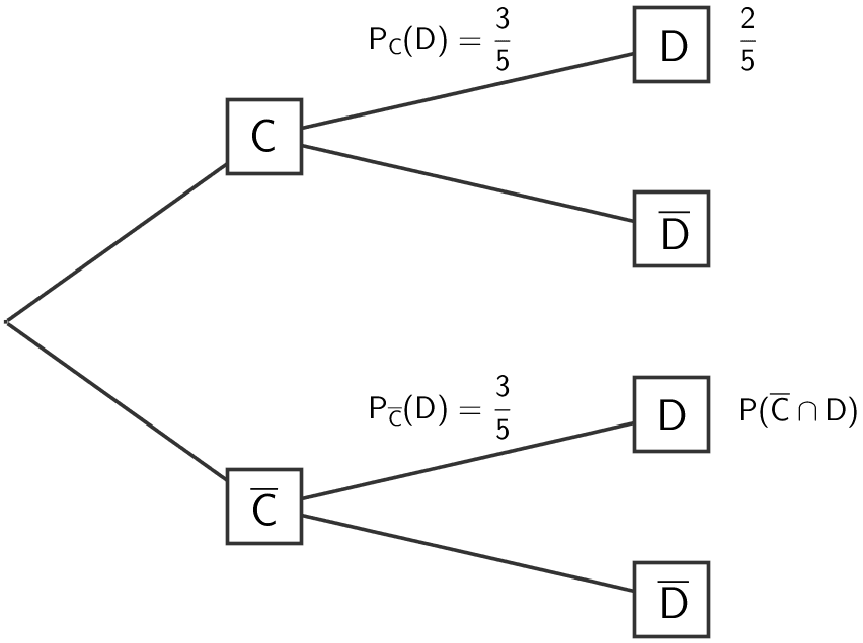
Baumdiagramm für stochastische Unabhängigkeit der Ereignisse \(C\) und \(D\)
Schnittmengenwahrscheinlichkeit \(P(\overline{C} \cap D)\) berechnen:
\(\displaystyle P(C) = \frac{2}{3}\) (siehe Teilaufgabe 1b)
Anwenden der zweiten Pfadregel und der Knotenregel:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[\begin{align*} P(\overline{C} \cap D) &= P(\overline{C}) \cdot P_{\overline{C}}(D) \\[0.8em] &= (1 - P(C)) \cdot P_{\overline{C}}(D) \\[0.8em] &= \left(1 - \frac{2}{3} \right) \cdot \frac{3}{5} \\[0.8em] &= \frac{1}{3} \cdot \frac{3}{5} \\[0.8em] &= \frac{1}{5} \end{align*}\]
Damit die Ereignisse \(C\) und \(D\) unabhängig sind, muss der Wert \(\displaystyle \frac{1}{10}\) für die Schnittmengenwahrscheinlichkeit \(P(\overline{C} \cap D)\) auf \(\displaystyle \frac{1}{5}\) geändert werden.
Probe:
Stochastische (Un)Abhängigkeit von zwei Ereignissen
Zwei Ereignisse \(A\) und \(B\) heißen stochastisch unabhängig, wenn
\(P(A) \cdot P(B) = P(A \cap B)\) gilt. (vgl. Merkhilfe) *
Andernfalls heißen die Ereignisse \(A\) und \(B\) stochastisch abhängig.
Sind zwei Ereignisse \(A\) und \(B\) stochastisch unabhängig, beeinflusst das Eintreten des Ereignisses \(A\) nicht das Eintreten des Ereignisses \(B\) und umgekehrt.
* Oder wenn
\(P(\overline{A}) \cdot P(B) = P(\overline{A} \cap B)\) bzw.
\(P(A) \cdot P(\overline{B}) = P(A \cap \overline{B})\) bzw.
\(P(\overline{A}) \cdot P(\overline{B}) = P(\overline{A} \cap \overline{B})\) gilt.
\(\displaystyle P(C \cap D) = \frac{2}{5}\,; \quad P(C) = \frac{2}{3}\) (siehe Teilaufgabe 2b)
\[\begin{align*}P(C) \cdot P(D) &= P(C) \cdot (P(C \cap D) + P(\overline{C} \cap D)) \\[0.8em] &= \frac{2}{3} \cdot \left( \frac{2}{5} + \frac{1}{5} \right) \\[0.8em] &= \frac{2}{3} \cdot \frac{3}{5} \\[0.8em] &= \frac{2}{5}\end{align*}\]
\[\Longrightarrow \quad P(C \cap D) = P(C) \cdot P(D)\]
\(\Longrightarrow \quad\) Die Ereignisse \(C\) und \(D\) sind unabhängig.
2.Lösungsansatz: Stochastische Unabhängigkeit formulieren
Es soll sich nur der Wert der Schnittmengenwahrscheinlichkeit \(\displaystyle P(\overline{C} \cap D) = \frac{1}{10}\) ändern. Die Wahrscheinlichkeiten \(\displaystyle P_{C}(D) = \frac{3}{5}\) und \(\displaystyle P(C \cap D) = \frac{2}{5}\) gelten weiterhin (siehe Abbildung zur Teilaufgabe 2).
Damit die Ereignisse \(C\) und \(D\) - und damit auch deren Gegenereignisse - unabhängig sind, muss für die Schnittmengenwahrscheinlichkeit \(P(\overline{C} \cap D)\) gelten:
\[P(\overline{C} \cap D) = P(\overline{C}) \cdot P(D)\]
Wahrscheinlichkeit \(P(\overline{C})\) berechnen:
\(\displaystyle P(C) = \frac{2}{3}\) (siehe Teilaufgabe 2b)
\[P(\overline{C}) = 1 - P(C) = 1 - \frac{2}{3} = \frac{1}{3}\]
Wahrscheinlichkeit \(P(D)\) berechnen:
\[\begin{align*}P(C \cap D) &= P(C) \cdot P(D) & &| : P(C) \\[0.8em] \frac{P(C \cap D)}{P(C)} &= P(D) \\[0.8em] \frac{\frac{2}{5}}{\frac{2}{3}} &= P(D) \\[0.8em] \frac{2}{5} \cdot \frac{3}{2} &= P(D) \\[0.8em] \frac{3}{5} &= P(D) \end{align*}\]
Wahrscheinlichkeit \(P(\overline{C} \cap D)\) berechnen:
\[P(\overline{C} \cap D) = P(\overline{C}) \cdot P(D) = \frac{1}{3} \cdot \frac{3}{5} = \frac{1}{5}\]
Damit die Ereignisse \(C\) und \(D\) unabhängig sind, muss der Wert \(\displaystyle \frac{1}{10}\) für die Schnittmengenwahrscheinlichkeit \(P(\overline{C} \cap D)\) auf \(\displaystyle \frac{1}{5}\) geändert werden.

