Stelle gleicher Steigung zweier Funktionsgraphen

Dieser Aufgabentyp gibt zwei differenzierbare Funktionen \(f\) und \(g\) vor (vgl. Abiturskript - 1.5.1 Die Ableitung, Differenzierbarkeit) und fragt nach derjenigen Stelle \(x_{0}\), an der die Funktionsgraphen \(G_{f}\) und \(G_{g}\) die gleiche Steigung besitzen.

 

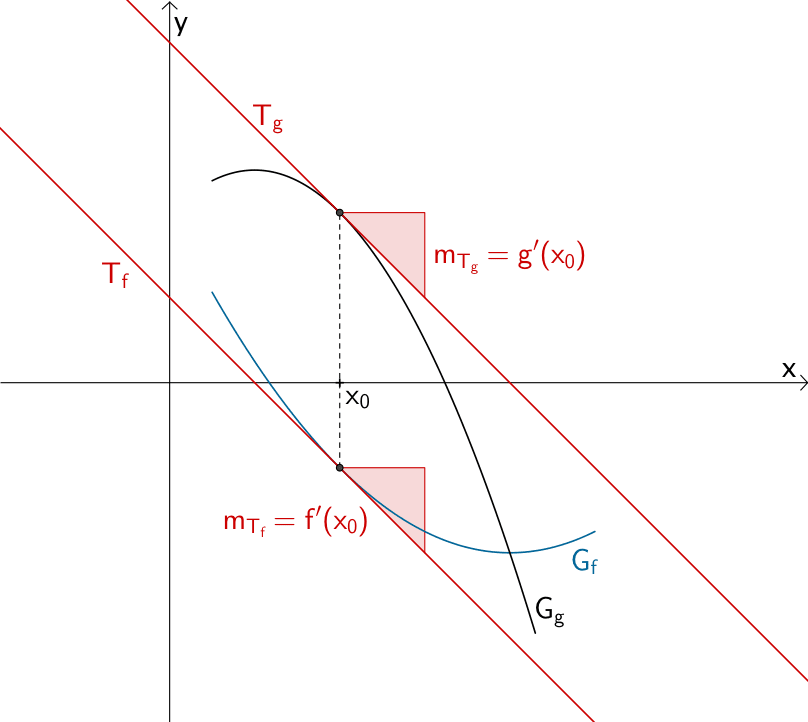
Stelle \(x_{0}\) mit gleicher Steigung zweier Funktionsgraphen \(G_{f}\) und \(G_{g}\)

 

Unter der Steigung eines Funktionsgraphen versteht man die Steigung der Tangente an den Funktionsgraphen an einer betrachteten Stelle \(x_{0}\). Die erste Ableitung einer Funktion an einer Stelle \(x_{0}\) ist gleich der Steigung \(m_{T}\) der Tangente an den Graphen der Funktion an der Stelle \(x_{0}\) (vgl. Abiturskript - 1.5.1 Die Ableitung, Tangentensteigung).

 

\[m_{T_{f}} = f'(x_{0})\]

\[m_{T_{g}} = g'(x_{0})\]

 

Folglich muss für die Gleichheit der Steigung zweier Funktionsgraphen \(G_{f}\) und \(G_{g}\) an einer Stelle \(x_{0}\) gelten:

 

\[\begin{align*}m_{T_{f}} &= m_{T_{g}} \\[0.8em] f'(x_{0}) &= g'(x_{0})\end{align*}\]

 

Sonderfall - Berührpunkt zweier Funktionsgraphen

Gilt für zwei differenzierbare Funktionen \(f\) und \(g\) an einer Stelle \(x_{0}\) die Bedingung \(f'(x_{0}) = g'(x_{0})\) und die Bedingung \(f(x_{0}) = g(x_{0})\), so berühren sich die Graphen der Funktionen \(f\) und \(g\) an der Stelle \(x_{0}\). Die Tangenten der Graphen \(f\) und \(g\) an der Stelle \(x_{0}\) sind dann identisch. (vgl. 1.5.9 Seite 3 - Berührpunkt zweier Funktionsgraphen)

 

Beispiel:

Gegeben seien die in \(\mathbb R\) definierten und differenzierbaren Funktionen \(f \colon x \mapsto e^{2x + 2} - 2\) und \(g \colon x \mapsto - \dfrac{4}{e^{4x + 4}} - 1\). Bestimmen Sie diejenige Stelle \(x_{0}\), an der die Tangente \(T_{f}\) an den Graphen \(G_{f}\) und die Tangente \(T_{g}\) an den Graphen \(G_{g}\) parallel zueinander verlaufen und geben Sie die Bedeutung der Stelle \(x_{0}\) an.

 

\[f(x) = e^{2x + 2} - 2; \; D_{f} = \mathbb R\]

\[g(x) = -\frac{4}{e^{4x + 4}} - 1; \; D_{g} = \mathbb R\]

 

Bestimmung der Stelle \(x_{0}\)

 

Steigungen der Tangenten \(T_{f}\) und \(T_{g}\) an der Stelle \(x_{0}\) (vgl. Abiturskript - 1.5.1 Die Ableitung, Tangentensteigung):

 

\[m_{T_{f}} = f'(x_{0})\]

\[m_{T_{g}} = g'(x_{0})\]

 

Die Tangente \(T_{f}\) an den Graphen \(G_{f}\) und die Tangente \(T_{g}\) an den Graphen \(T_{g}\) verlaufen an der Stelle \(x_{0}\) parallel zueinander, wenn sie dort die gleiche Steigung haben.

 

Bedingung für die Gleichheit der Tangentensteigungen an der Stelle \(x_{0}\):

 

\[\begin{align*}m_{T_{f}} &= m_{T_{g}} \\[0.8em] f'(x) &= g'(x) \end{align*}\]

 

Erste Ableitung \(f'\) und \(g'\) bilden (vgl. Abiturskript - 1.5.2 Ableitungsregeln):

Der Funktionsterm \(f(x)\) kann mithilfe der Ableitung der Natürlichen Exponentialfunktion und der Kettenregel abgeleitet werden. Der Funktionsterm \(g(x)\) lässt sich vorab in der Potenzschreibweise formulieren. Die Ableitung \(g'(x)\) ergibt sich anschließend mithilfe der Faktorregel, der Ableitung der Natürlichen Exponentialfunktion und der Kettenregel (Alternative: Quotientenregel anwenden).

 

\[f(x) = e^{2x + 2} - 2\]

 

\[f'(x) = e^{2x + 2} \cdot 2 - 0 = 2e^{2x + 2}\]

 

\[\begin{align*}g(x) &= -\frac{4}{e^{4x + 4}} - 1 & &| \; \frac{1}{a^{n}} = a^{-n} \\[0.8em] &= -4e^{-(4x + 4)} - 1 \\[0.8em] &= -4e^{-4x - 4} - 1 \end{align*}\]

 

\[g'(x) = (-4) \cdot e^{-4x - 4} \cdot (-4) - 0 = 16e^{-4x - 4}\]

 

Stelle \(x_{0}\) mit gleicher Steigung der Tangenten \(T_{f}\) und \(T_{g}\) berechnen:

 

\[\begin{align*}m_{T_{f}} &= m_{T_{g}} \\[0.8em] f'(x) &= g'(x) \\[0.8em] 2e^{2x+2} &= 16e^{-4x-4} \end{align*}\]

 

Die Exponentialgleichung lässt sich mithilfe der Logarithmenregel \(\log_{a}(b \cdot c) = \log_{a}b + \log_{a}c\) durch Logarithmieren lösen (vgl. Abiturskript - 1.3.1 Eigenschaften und Rechenregeln, Natürliche Exponential- und Logarithmusfunktion sowie Abiturskript - 1.3.3 Exponential- und Logarithmusgleichungen).

 

\[\begin{align*}2e^{2x+2} &= 16e^{-4x-4} : 2 \\[0.8em] e^{2x+2} &= 8e^{-4x-4} & &| \; \ln(\dots) \enspace \text{Logarithmieren} \\[0.8em] \ln\left( e^{2x-2} \right) &= \ln\left( 8e^{-4x-4} \right) & &| \; \ln e^{x} = x; \enspace \log_{a}(b \cdot c) = \log_{a}b + \log_{a}c \\[0.8em] 2x + 2 &= \ln{8} -4x - 4 & &| + 4x - 2 \\[0.8em] 6x &= \ln{8} - 6 \\[0.8em] 6x &= \ln\left( 2^{3} \right) - 6 & &| \; \log_{a}(b^{n}) = n \cdot \log_{a}{b} \\[0.8em] 6x &= 3\ln2 - 6 & &| : 6 \\[0.8em] x &= \frac{\ln{2}}{2} - 1 \\[0.8em] x &\approx 0{,}65 \end{align*}\]

 

Die Tangenten an die Graphen der Funktionen \(f\) und \(g\) an der Stelle \(x_{0} = \dfrac{\ln{2}}{2} - 1\) haben die gleiche Steigung. Die Tangenten können somit (echt) parallel zueinander verlaufen oder identisch sein (Berührpunkt von \(G_{f}\) und \(G_{g}\)).

 

Sonderfall identischer Tangenten (eines Berührpunkts) überprüfen:

Damit die Tangenten an die Graphen der Funktionen \(f\) und \(g\) an der Stelle \(x_{0}\) (echt) parallel zueinander verlaufen, muss \(f(x_{0}) \neq g(x_{0})\) gelten.

 

\[f(x) = e^{2x+2} - 2\]

\[g(x) = -\frac{4}{e^{4x+4}} - 1 = -4e^{-4x-4} - 1\]

\[x_{0} = \frac{\ln{2}}{2} - 1\]

 

\[\begin{align*} f(x_{0}) &= e^{\left[2 \cdot \left( \frac{\ln{2}}{2} - 1 \right) +2 \right]} - 2 \\[0.8em] &= e^{\ln{2} - 2 + 2} - 2 \\[0.8em] &= e^{\ln{2}} - 2 & &| \; e^{\ln{x}} = x \\[0.8em] &= 2 - 2 \\[0.8em] &= 0 \end{align*}\]

 

\[\begin{align*} g(x_{0}) &= -4e^{\left[ (-4) \cdot \left( \frac{\ln{2}}{2} - 1 \right) -4 \right]} - 1 \\[0.8em] &= -4e^{-2\ln{2} + 4 - 4} - 1 \\[0.8em] &= -4e^{-2\ln{2}} - 1 & &| \; a^{m \cdot n} = \left( a^{m} \right)^{n} \\[0.8em] &= (-4) \cdot \left( e^{\ln{2}} \right)^{-2} - 1 & &| \; e^{\ln{x}} = x \\[0.8em] &= (-4) \cdot 2^{-2} - 1 & &| \; a^{-n} = \frac{1}{a^{n}} \\[0.8em] &= (-4) \cdot \frac{1}{2^{2}} - 1 \\[0.8em] &= -2 \end{align*}\]

 

\[\Longrightarrow \quad f(x_{0}) \neq g(x_{0})\]

 

An der Stelle \(x_{0} = \dfrac{\ln{2}}{2} - 1\) verlaufen die Tangenten an die Graphen der Funktionen \(f\) und \(g\) (echt) parallel zueinander.

 

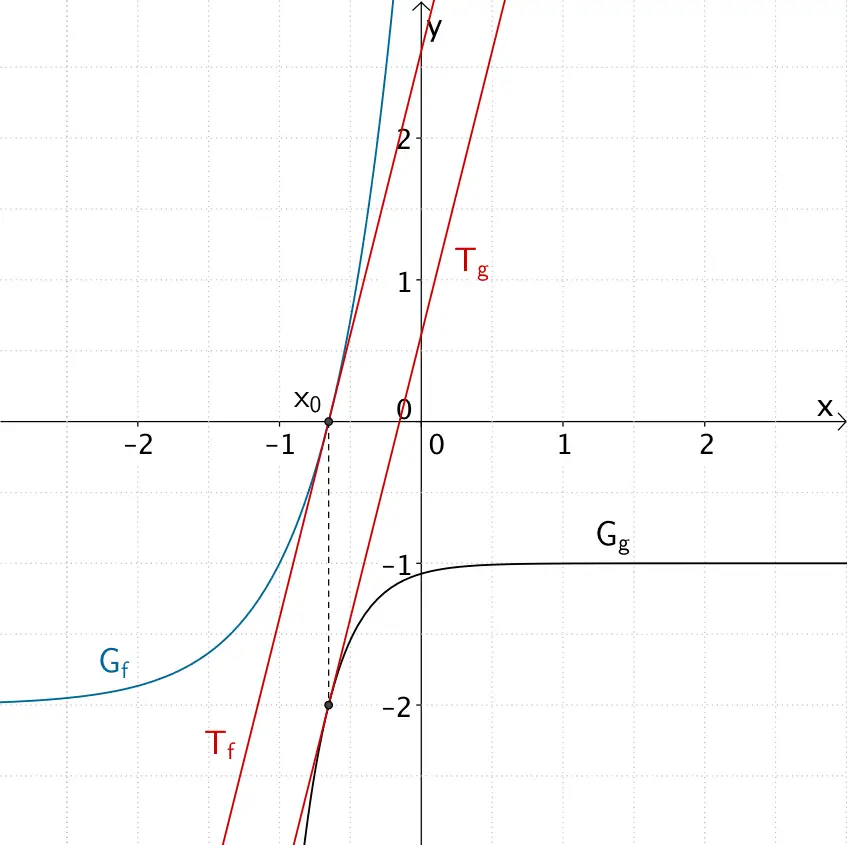
Stelle \(x_{0} = \dfrac{\ln{2}}{2} - 1\), an der die Tangente \(T_{f}\) an den Graphen der Funktion \(f \colon x \mapsto e^{2x+2}-2\) und die Tangente \(T_{g}\) an den Graphen der Funktion \(g \colon x \mapsto -\dfrac{4}{e^{4x+4}} - 1\) (echt) parallel zueinander verlaufen.

 

Bedeutung der Stelle \(x_{0}\) 

An der Stelle \(x_{0} = \dfrac{\ln{2}}{2} - 1\) besitzt der Graph \(G_{f}\) der Funktion \(f\) und der Graph \(G_{g}\) der Funktion \(g\) die gleiche Steigung. Die Graphen berühren sich nicht.