Stelle gleicher Steigung zweier Funktionsgraphen
Dieser Aufgabentyp gibt zwei differenzierbare Funktionen \(f\) und \(g\) vor (vgl. Abiturskript - 1.5.1 Die Ableitung, Differenzierbarkeit) und fragt nach derjenigen Stelle \(x_{0}\), an der die Funktionsgraphen \(G_{f}\) und \(G_{g}\) die gleiche Steigung besitzen.
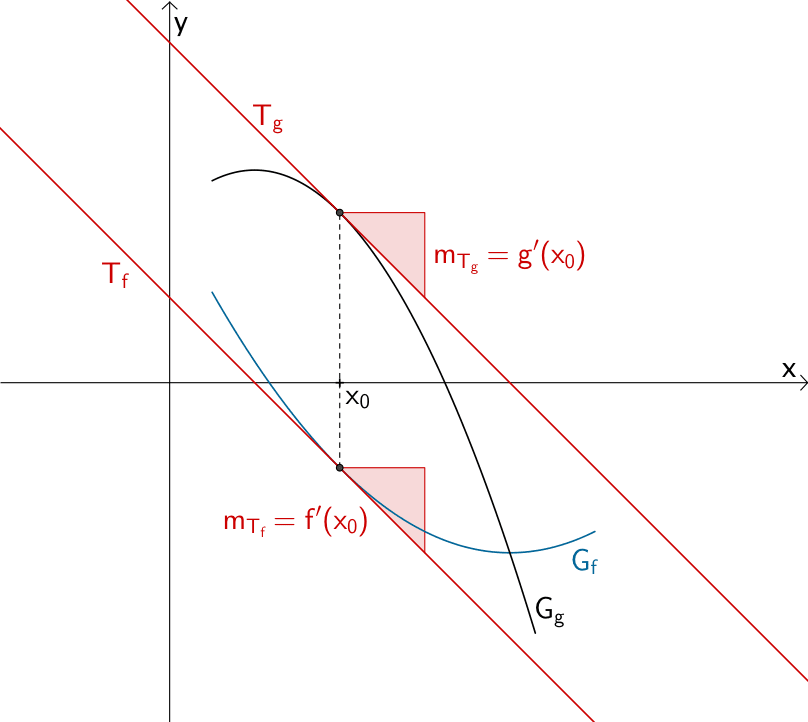
Stelle \(x_{0}\) mit gleicher Steigung zweier Funktionsgraphen \(G_{f}\) und \(G_{g}\)
Unter der Steigung eines Funktionsgraphen versteht man die Steigung der Tangente an den Funktionsgraphen an einer betrachteten Stelle \(x_{0}\). Die erste Ableitung einer Funktion an einer Stelle \(x_{0}\) ist gleich der Steigung \(m_{T}\) der Tangente an den Graphen der Funktion an der Stelle \(x_{0}\) (vgl. Abiturskript - 1.5.1 Die Ableitung, Tangentensteigung).
\[m_{T_{f}} = f'(x_{0})\]
\[m_{T_{g}} = g'(x_{0})\]
Folglich muss für die Gleichheit der Steigung zweier Funktionsgraphen \(G_{f}\) und \(G_{g}\) an einer Stelle \(x_{0}\) gelten:
\[\begin{align*}m_{T_{f}} &= m_{T_{g}} \\[0.8em] f'(x_{0}) &= g'(x_{0})\end{align*}\]
Sonderfall - Berührpunkt zweier Funktionsgraphen
Gilt für zwei differenzierbare Funktionen \(f\) und \(g\) an einer Stelle \(x_{0}\) die Bedingung \(f'(x_{0}) = g'(x_{0})\) und die Bedingung \(f(x_{0}) = g(x_{0})\), so berühren sich die Graphen der Funktionen \(f\) und \(g\) an der Stelle \(x_{0}\). Die Tangenten der Graphen \(f\) und \(g\) an der Stelle \(x_{0}\) sind dann identisch. (vgl. 1.5.9 Seite 3 - Berührpunkt zweier Funktionsgraphen)
Beispiel:
Gegeben seien die in \(\mathbb R\) definierten und differenzierbaren Funktionen \(f \colon x \mapsto e^{2x + 2} - 2\) und \(g \colon x \mapsto - \dfrac{4}{e^{4x + 4}} - 1\). Bestimmen Sie diejenige Stelle \(x_{0}\), an der die Tangente \(T_{f}\) an den Graphen \(G_{f}\) und die Tangente \(T_{g}\) an den Graphen \(G_{g}\) parallel zueinander verlaufen und geben Sie die Bedeutung der Stelle \(x_{0}\) an.
\[f(x) = e^{2x + 2} - 2; \; D_{f} = \mathbb R\]
\[g(x) = -\frac{4}{e^{4x + 4}} - 1; \; D_{g} = \mathbb R\]
Bestimmung der Stelle \(x_{0}\)
Steigungen der Tangenten \(T_{f}\) und \(T_{g}\) an der Stelle \(x_{0}\) (vgl. Abiturskript - 1.5.1 Die Ableitung, Tangentensteigung):
\[m_{T_{f}} = f'(x_{0})\]
\[m_{T_{g}} = g'(x_{0})\]
Die Tangente \(T_{f}\) an den Graphen \(G_{f}\) und die Tangente \(T_{g}\) an den Graphen \(T_{g}\) verlaufen an der Stelle \(x_{0}\) parallel zueinander, wenn sie dort die gleiche Steigung haben.
Bedingung für die Gleichheit der Tangentensteigungen an der Stelle \(x_{0}\):
\[\begin{align*}m_{T_{f}} &= m_{T_{g}} \\[0.8em] f'(x) &= g'(x) \end{align*}\]
Erste Ableitung \(f'\) und \(g'\) bilden (vgl. Abiturskript - 1.5.2 Ableitungsregeln):
Der Funktionsterm \(f(x)\) kann mithilfe der Ableitung der Natürlichen Exponentialfunktion und der Kettenregel abgeleitet werden. Der Funktionsterm \(g(x)\) lässt sich vorab in der Potenzschreibweise formulieren. Die Ableitung \(g'(x)\) ergibt sich anschließend mithilfe der Faktorregel, der Ableitung der Natürlichen Exponentialfunktion und der Kettenregel (Alternative: Quotientenregel anwenden).
\[f(x) = e^{2x + 2} - 2\]
\[f'(x) = e^{2x + 2} \cdot 2 - 0 = 2e^{2x + 2}\]
\[\begin{align*}g(x) &= -\frac{4}{e^{4x + 4}} - 1 & &| \; \frac{1}{a^{n}} = a^{-n} \\[0.8em] &= -4e^{-(4x + 4)} - 1 \\[0.8em] &= -4e^{-4x - 4} - 1 \end{align*}\]
\[g'(x) = (-4) \cdot e^{-4x - 4} \cdot (-4) - 0 = 16e^{-4x - 4}\]
Stelle \(x_{0}\) mit gleicher Steigung der Tangenten \(T_{f}\) und \(T_{g}\) berechnen:
\[\begin{align*}m_{T_{f}} &= m_{T_{g}} \\[0.8em] f'(x) &= g'(x) \\[0.8em] 2e^{2x+2} &= 16e^{-4x-4} \end{align*}\]
Die Exponentialgleichung lässt sich mithilfe der Logarithmenregel \(\log_{a}(b \cdot c) = \log_{a}b + \log_{a}c\) durch Logarithmieren lösen (vgl. Abiturskript - 1.3.1 Eigenschaften und Rechenregeln, Natürliche Exponential- und Logarithmusfunktion sowie Abiturskript - 1.3.3 Exponential- und Logarithmusgleichungen).
\[\begin{align*}2e^{2x+2} &= 16e^{-4x-4} : 2 \\[0.8em] e^{2x+2} &= 8e^{-4x-4} & &| \; \ln(\dots) \enspace \text{Logarithmieren} \\[0.8em] \ln\left( e^{2x-2} \right) &= \ln\left( 8e^{-4x-4} \right) & &| \; \ln e^{x} = x; \enspace \log_{a}(b \cdot c) = \log_{a}b + \log_{a}c \\[0.8em] 2x + 2 &= \ln{8} -4x - 4 & &| + 4x - 2 \\[0.8em] 6x &= \ln{8} - 6 \\[0.8em] 6x &= \ln\left( 2^{3} \right) - 6 & &| \; \log_{a}(b^{n}) = n \cdot \log_{a}{b} \\[0.8em] 6x &= 3\ln2 - 6 & &| : 6 \\[0.8em] x &= \frac{\ln{2}}{2} - 1 \\[0.8em] x &\approx 0{,}65 \end{align*}\]
Die Tangenten an die Graphen der Funktionen \(f\) und \(g\) an der Stelle \(x_{0} = \dfrac{\ln{2}}{2} - 1\) haben die gleiche Steigung. Die Tangenten können somit (echt) parallel zueinander verlaufen oder identisch sein (Berührpunkt von \(G_{f}\) und \(G_{g}\)).
Sonderfall identischer Tangenten (eines Berührpunkts) überprüfen:
Damit die Tangenten an die Graphen der Funktionen \(f\) und \(g\) an der Stelle \(x_{0}\) (echt) parallel zueinander verlaufen, muss \(f(x_{0}) \neq g(x_{0})\) gelten.
\[f(x) = e^{2x+2} - 2\]
\[g(x) = -\frac{4}{e^{4x+4}} - 1 = -4e^{-4x-4} - 1\]
\[x_{0} = \frac{\ln{2}}{2} - 1\]
\[\begin{align*} f(x_{0}) &= e^{\left[2 \cdot \left( \frac{\ln{2}}{2} - 1 \right) +2 \right]} - 2 \\[0.8em] &= e^{\ln{2} - 2 + 2} - 2 \\[0.8em] &= e^{\ln{2}} - 2 & &| \; e^{\ln{x}} = x \\[0.8em] &= 2 - 2 \\[0.8em] &= 0 \end{align*}\]
\[\begin{align*} g(x_{0}) &= -4e^{\left[ (-4) \cdot \left( \frac{\ln{2}}{2} - 1 \right) -4 \right]} - 1 \\[0.8em] &= -4e^{-2\ln{2} + 4 - 4} - 1 \\[0.8em] &= -4e^{-2\ln{2}} - 1 & &| \; a^{m \cdot n} = \left( a^{m} \right)^{n} \\[0.8em] &= (-4) \cdot \left( e^{\ln{2}} \right)^{-2} - 1 & &| \; e^{\ln{x}} = x \\[0.8em] &= (-4) \cdot 2^{-2} - 1 & &| \; a^{-n} = \frac{1}{a^{n}} \\[0.8em] &= (-4) \cdot \frac{1}{2^{2}} - 1 \\[0.8em] &= -2 \end{align*}\]
\[\Longrightarrow \quad f(x_{0}) \neq g(x_{0})\]
An der Stelle \(x_{0} = \dfrac{\ln{2}}{2} - 1\) verlaufen die Tangenten an die Graphen der Funktionen \(f\) und \(g\) (echt) parallel zueinander.
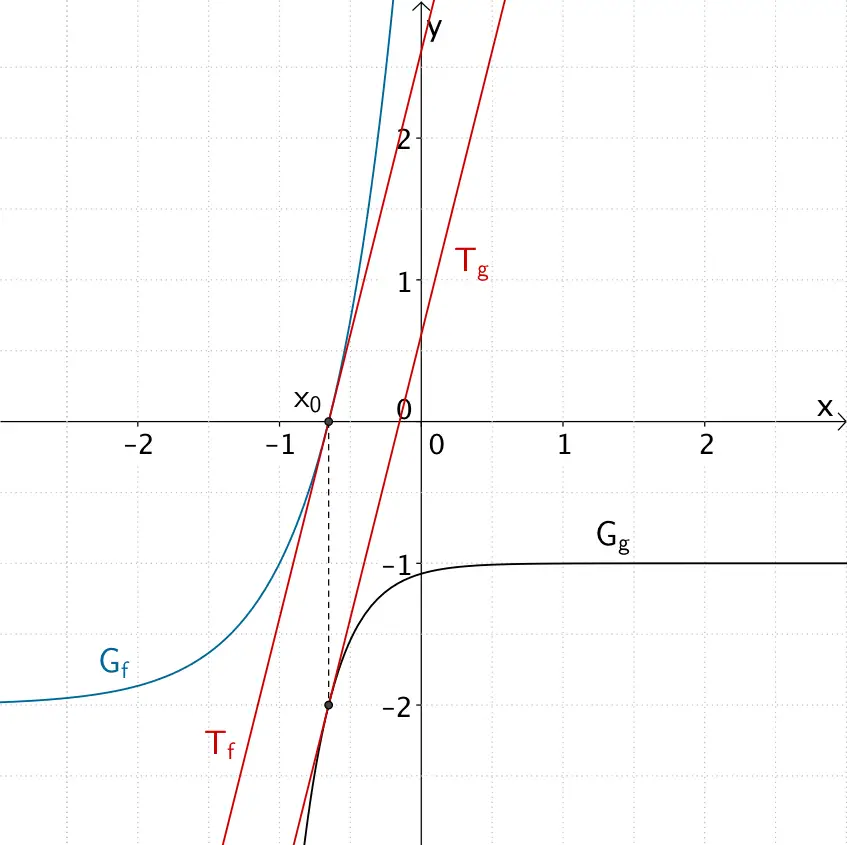
Stelle \(x_{0} = \dfrac{\ln{2}}{2} - 1\), an der die Tangente \(T_{f}\) an den Graphen der Funktion \(f \colon x \mapsto e^{2x+2}-2\) und die Tangente \(T_{g}\) an den Graphen der Funktion \(g \colon x \mapsto -\dfrac{4}{e^{4x+4}} - 1\) (echt) parallel zueinander verlaufen.
Bedeutung der Stelle \(x_{0}\)
An der Stelle \(x_{0} = \dfrac{\ln{2}}{2} - 1\) besitzt der Graph \(G_{f}\) der Funktion \(f\) und der Graph \(G_{g}\) der Funktion \(g\) die gleiche Steigung. Die Graphen berühren sich nicht.
Stelle orthogonaler Tangenten zweier Funktionsgraphen
Dieser Aufgabentyp gibt zwei differenzierbare Funktionen \(f\) und \(g\) vor (vgl. Abiturskript - 1.5.1 Die Ableitung, Differenzierbarkeit) und fragt nach derjenigen Stelle \(x_{0}\), an der die Tangenten an die Funktionsgraphen \(G_{f}\) und \(G_{g}\) orthogonal (zueinander senkrecht) sind.
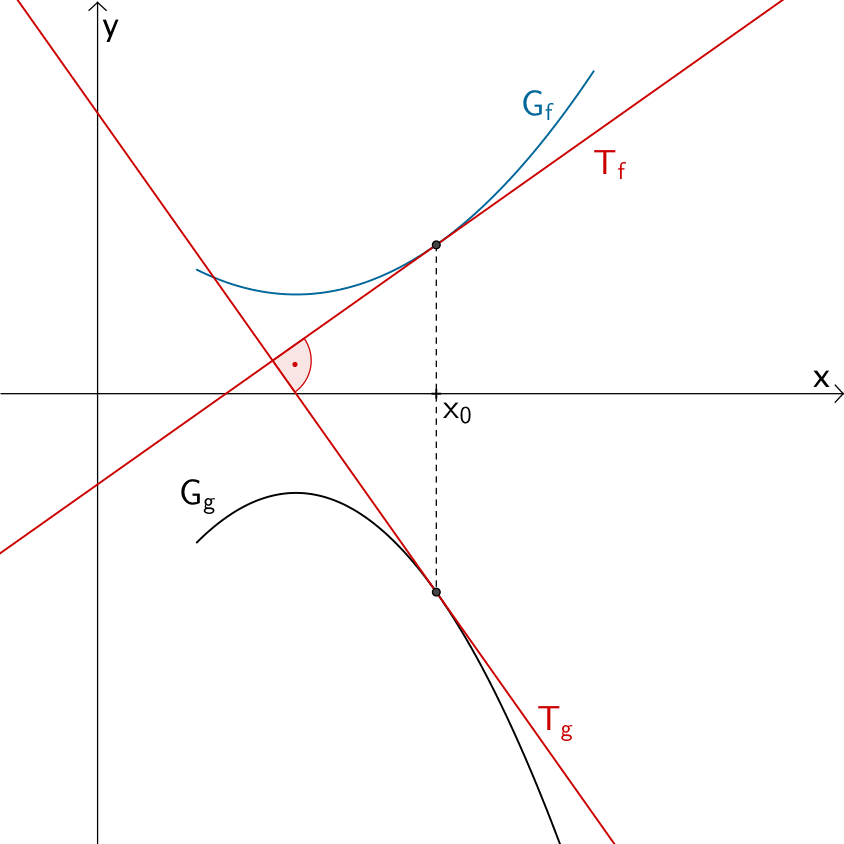
Stelle \(x_{0}\), an der Die Tangenten der Graphen zweier Funktionen \(f\) und \(g\) orthogonal (zueinander senkrecht) sind.
Die erste Ableitung einer Funktion an einer Stelle \(x_{0}\) ist gleich der Steigung \(m_{T}\) der Tangente an den Graphen der Funktion an der Stelle \(x_{0}\) (vgl. Abiturskript - 1.5.1 Die Ableitung, Tangentensteigung).
\[m_{T_{f}} = f'(x_{0})\]
\[m_{T_{g}} = g'(x_{0})\]
Für die Steigungen \(m_{1}\) und \(m_{2}\) zweier zueinander senkrechter Geraden gilt: \(m_{1} \cdot m_{2} = -1 \enspace \Leftrightarrow \enspace m_{1} = -\dfrac{1}{m_{2}}\) (vgl. Abiturskript - 1.1.1 Lineare Funktion, Steigung einer Geraden).
Folglich muss für die Orthogonalität der Tangenten \(T_{f}\) und \(T_{g}\) zweier Funktionsgraphen \(G_{f}\) und \(G_{g}\) an einer Stelle \(x_{0}\) gelten:
\[\begin{align*} m_{T_{f}} &= -\frac{1}{m_{T_{g}}} \\[0.8em] f'(x_{0}) &= -\frac{1}{g'(x_{0})} \end{align*}\]
Beispiel:
Gegeben seien die in \(\mathbb R\) definierten und diferenzierbaren Funktionen \(f \colon x \mapsto 0{,}25x^{2} + 2x - 4\) und \(g \colon x \mapsto -0{,}5x^{2} - 2x + 4\). Ermitteln Sie diejenigen Stellen, an denen die Tangenten der Graphen der Funktionen \(f\) und \(g\) orthogonal sind.
\[f(x) = 0{,}25x^{2} + 2x - 4; \; D_{f} = \mathbb R\]
\[g(x) = -0{,}5x^{2} - 2x + 4; \; D_{g} = \mathbb R\]
Steigungen der Tangenten \(T_{f}\) und \(T_{g}\) (vgl. Abiturskript - 1.5.1 Die Ableitung, Tangentensteigung):
\[m_{T_{f}} = f'(x)\]
\[m_{T_{g}} = g'(x)\]
Bedingung für die Orthogonalität der Tangenten an die Graphen der Funktionen \(f\) und \(g\):
\[\begin{align*} m_{T_{f}} &= -\frac{1}{m_{T_{g}}} \\[0.8em] f'(x_{0}) &= -\frac{1}{g'(x_{0})} \end{align*}\]
Erste Ableitung \(f'\) und \(g'\) bilden (vgl. Abiturskript - 1.5.2 Ableitungsregeln):
Die Erste Ableitung der Funktionsterme \(f(x)\) und \(g(x)\) lässt sich mithilfe der Faktorregel, der Summenregel und der Ableitung einer Potenzfunktion formulieren.
\[f(x) = 0{,}25x^{2} + 2x - 4\]
\[f'(x) = 0{,}25 \cdot 2 \cdot x + 2 = 0{,}5x + 2\]
\[g(x) = -0{,}5x^{2} - 2x + 4\]
\[g'(x) = -0{,}5 \cdot 2 \cdot x - 2 = -x - 2\]
Stellen orthogonaler Tangenten \(T_{f}\) und \(T_{g}\) berechnen:
\[\begin{align*} m_{T_{f}} &= -\frac{1}{m_{T_{g}}} \\[0.8em] f'(x_{0}) &= -\frac{1}{g'(x_{0})} \\[0.8em] 0{,}5x + 2 &= -\frac{1}{-x - 2}\end{align*}\]
Der Nennerterm \(-x - 2\) darf nicht gleich Null sein. Als mögliche Lösungen kommen somit alle \(x \in \mathbb R \backslash \{-2\}\) in Frage.
Die Bruchgleichung wird zunächst mit dem Nennerterm \(-x - 2\) multipliziert. Aus der entstehenden Gleichung wird eine quadratische Gleichung formuliert und darauf die Lösungsformel für quadratische Gleichungen angewendet (vgl. Abiturskript - 1.1.2 Quadratische Funktion, Lösungsformel für quadratische Gleichungen).
\[\begin{align*} 0{,}5x + 2 &= -\frac{1}{-x - 2} & &| \cdot (-x - 2) \\[0.8em] (0{,}5x + 2) \cdot (-x - 2) &= -1 \\[0.8em] -0{,}5x^{2} - x - 2x - 4 &= -1 \\[0.8em] -0{,}5x^{2} - 3x - 4 &= - 1 & &| + 1 \\[0.8em] -0{,}5x^{2} - 3x - 3 &= 0 \end{align*}\]
Lösungsformel für quadratische Gleichungen anwenden:
\[\begin{align*} x_{1,2} &= \frac{3 \pm \sqrt{(-3)^{2} - 4 \cdot (-0{,}5) \cdot (-3)}}{2 \cdot (-0{,}5)} \\[0.8em] &= \frac{3 \pm \sqrt{9 - 6}}{-1} \\[0.8em] &= -3 \pm \sqrt{3} \end{align*}\]
\[x_{1} = -3 - \sqrt{3} \approx -4{,}73\]
\[x_{2} = -3 + \sqrt{3} \approx -1{,}27\]
An den Stellen \(x_{1} = -3 -\sqrt{3}\) und \(x_{2} = -3 + \sqrt{3}\) sind die Tangenten \(T_{f}\) und \(T_{g}\) der Graphen der Funktionen \(f\) und \(g\) jeweils orthogonal (senkrecht zueinander).
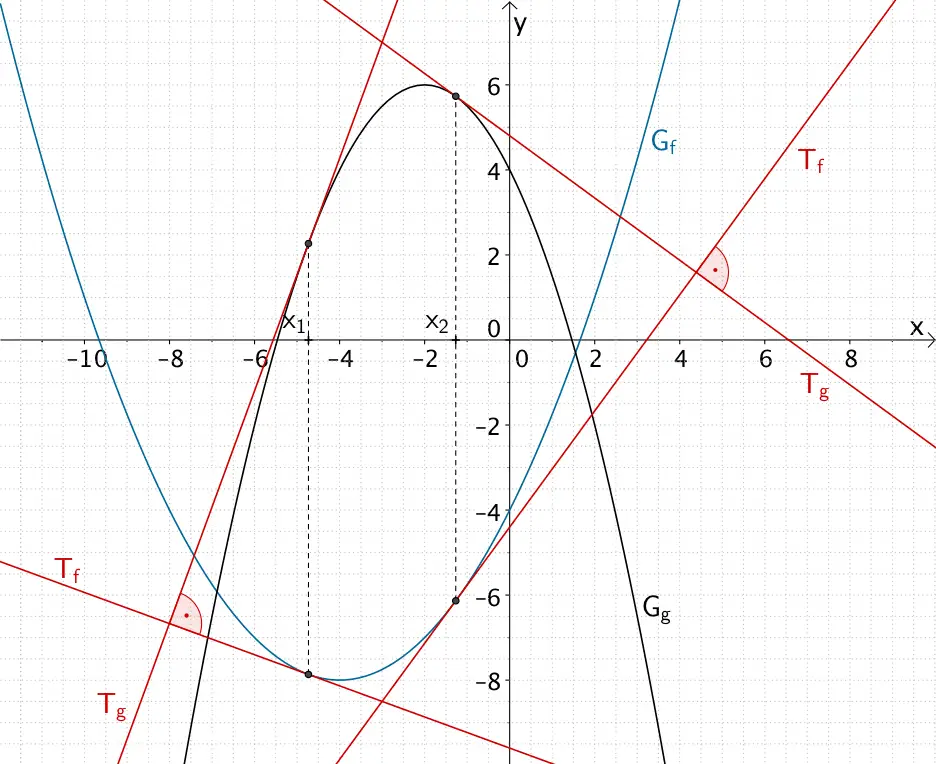
Stellen \(x_{1} = -3 - \sqrt{3}\) und \(x_{2} = -3 + \sqrt{3}\), an denen die Tangenten \(T_{f}\) und \(T_{g}\) der Graphen der Funktionen \(f \colon x \mapsto 0{,}25x^{2} + 2x - 4\) und \(g \colon x \mapsto -0{,}5x^{2} - 2x + 4\) jeweils orthogonal (senkrecht zueinander) sind.
Berührpunkt zweier Funktionsgraphen
Ein Berührpunkt der Funktionsgraphen zweier gegebener Funktionen \(f\) und \(g\) erfüllt zwei Bedingungen. Einmal stimmen die Steigungen der Graphen der Funktionen \(f\) und \(g\) an der Stelle \(x_{0}\) des Berührpunkts überein. Und zugleich stimmen die Funktionswerte der Funktionen \(f\) und \(g\) an der Stelle \(x_{0}\) des Berührpunkts überein. Die Graphen der Funktionen \(f\) und \(g\) besitzen somit im Berührpunkt eine gemeinsame Tangente.
Die erste Ableitung einer Funktion an einer Stelle \(x_{0}\) ist gleich der Steigung \(m_{T}\) der Tangente an den Graphen der Funktion an der Stelle \(x_{0}\) (vgl. Abiturskript - 1.5.1 Die Ableitung, Tangentensteigung).
\[m_{T_{f}} = f'(x)\]
\[m_{T_{g}} = g'(x)\]
1. Bedingung: Gleiche Steigung der Graphen \(\boldsymbol{G_{f}}\) und \(\boldsymbol{G_{g}}\) an einer Stelle \(\boldsymbol{x_{0}}\)
\[\begin{align*}m_{T_{f}} &= m_{T_{g}} \\[0.8em] f'(x_{0}) &= g'(x_{0})\end{align*}\]
(vgl. 1.5.9 Seite 1 - Stelle mit gleicher Steigung zweier Funktionsgraphen)
2. Bedingung: Gemeinsamer Punkt der Graphen \(\boldsymbol{G_{f}}\) und \(\boldsymbol{G_{g}}\) an der Stelle \(\boldsymbol{x_{0}}\)
\[f(x_{0}) = g(x_{0})\]
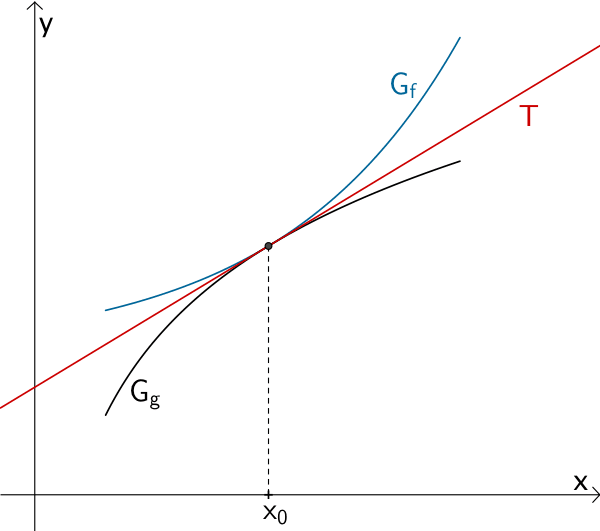
Im Falle eines Berührpunkts besitzen die Graphen \(G_{f}\) und \(G_{g}\) an der Stelle \(x_{0}\) eine gemeinsame Tangente \(T\) und es gilt: \(f'(x_{0}) = g'(x_{0})\).
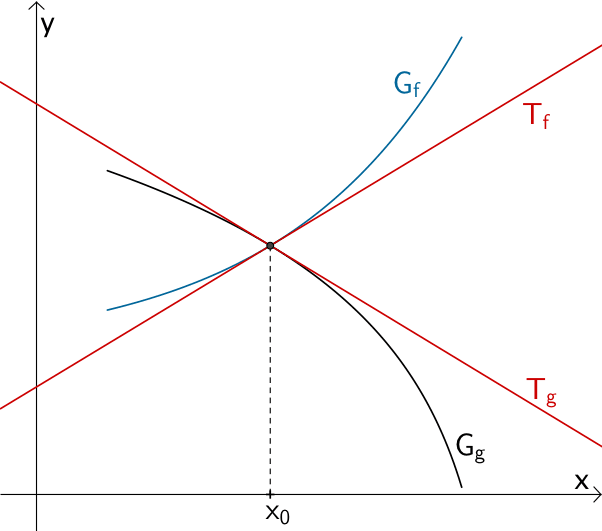
Im Falle eines Schnittpunkts besitzen die Graphen \(G_{f}\) und \(G_{g}\) an der Stelle \(x_{0}\) verschiedene Tangenten \(T_{f}\) und \(T_{g}\) und es gilt: \(f'(x_{0}) \neq g'(x_{0})\).
Vorgehensweise - Bestimmung eines Berührpunkts
In einem ersten Schritt wird die Gleichung \(f'(x) = g'(x)\) nach \(x\) aufgelöst. Jede Lösung der Gleichung ist eine mögliche Stelle \(x_{0}\) eines Berührpunkts.
Anschließend wird die Gültigkeit der Gleichung \(f(x_{0}) = g(x_{0})\) überprüft. Gilt \(f(x_{0}) = g(x_{0})\), liegt an der Stelle \(x_{0}\) eine Berührpunkt vor. Gilt \(f(x_{0}) \neq g(x_{0})\), besitzen die Graphen der Funktion \(f\) und \(g\) an der Stelle \(x_{0}\) die gleiche Steigung, ohne sich zu berühren (vgl. 1.5.9 Seite 1 - Stelle mit gleicher Steigung zweier Funktionsgraphen).

Graphen zweier Funktionen \(f\) und \(g\) mit einem Berührpunkt an der Stelle \(x_{0}\). Es gilt: \(f(x_{0}) = g(x_{0})\)
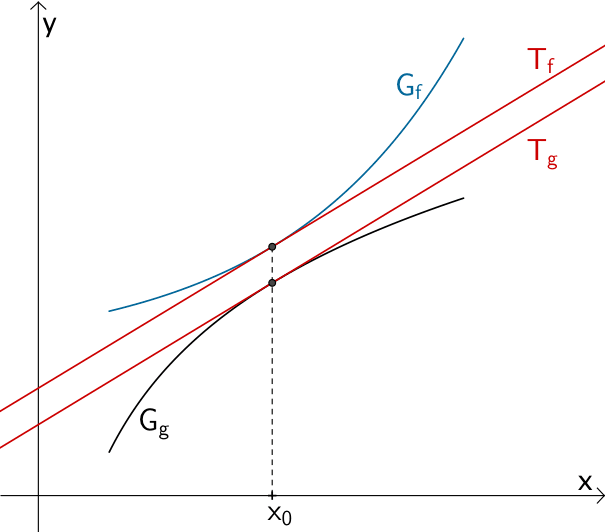
Graphen zweier Funktionen \(f\) und \(g\) mit gleicher Steigung an der Stelle \(x_{0}\) ohne Berührpunkt. Es gilt: \(f(x_{0}) \neq g(x_{0})\)
Beispiel:
Gegeben sei die Funktionen \(f \colon x \mapsto \dfrac{4}{x^{2}}\) mit maximalem Definitionsbereich \(D_{f} = \mathbb R \backslash \{0\}\) sowie die in \(\mathbb R\) definierte Funktion \(g \colon x \mapsto -\dfrac{1}{4}x^{2} + 2\). Überprüfen Sie rechnerisch, ob sich die Graphen \(G_{f}\) und \(G_{g}\) der Funktionen \(f\) und \(g\) berühren.
\[f(x) = \frac{4}{x^{2}}; \; D_{f} = \mathbb R \backslash \{0\}\]
\[g(x) = -\frac{1}{4}x^{2} + 2; \; D_{g} = \mathbb R\]
Ansatz für Stellen gleicher Steigung von \(G_{f}\) und \(G_{g}\):
Die Steigung \(m_{T_{f}}\) einer Tangente \(T_{f}\) an den Graphen \(G_{f}\) und die Steigung \(m_{T_{g}}\) einer Tangente \(T_{g}\) an den Graphen \(G_{g}\) müssen gleich groß sein. Die Funktionsterme \(f'(x)\) und \(g'(x)\) beschreiben die Tangentensteigung der Tangenten an die Graphen \(G_{f}\) und \(G_{g}\).
\[\begin{align*}m_{T_{f}} &= m_{T_{g}} \\[0.8em] f'(x) &= g'(x)\end{align*}\]
Erste Ableitung \(f'\) und \(g'\) bilden (vgl. Abiturskript - 1.5.2 Ableitungsregeln):
Der Funktionsterm \(f(x)\) kann in der Potenzschreibweise formuliert werden und lässt sich anschließend mithilfe der Faktorregel, und der Ableitung einer Potenzfunktion ableiten (Alternative: Quotientenregel anwenden). Die Ableitung des Funktionsterms \(g(x)\) erfolgt mithilfe der Faktorregel, der Summenregel und der Ableitung einer Potenzfunktion.
\[f(x) = \frac{4}{x^{2}} = 4x^{-2}\]
\[f'(x) = 4 \cdot (-2) \cdot x^{-3} = -8x^{-3} = -\frac{8}{x^{3}}\]
\[g(x) = -\frac{1}{4}x^{2} + 2\]
\[g'(x) = -\frac{1}{4} \cdot 2 \cdot x + 0 = -\frac{1}{2}x \]
Stellen gleicher Steigung der Graphen \(G_{f}\) und \(G_{g}\) berechnen:
\[\begin{align*}f'(x) &= g'(x) \\[0.8em] -\frac{8}{x^{3}} &= -\frac{1}{2}x^{2} & &| \cdot x^{3} \\[0.8em] -8 &= -\frac{1}{2}x^{4} & &| \cdot (-2) \\[0.8em] 16 &= x^{4} & &| \; \sqrt[4]{\quad} \\[0.8em] \pm 2 &= x_{1,2} \end{align*}\]
An den Stellen \(x_{1} = -2\) und \(x_{2} = 2\) besitzen die Graphen der Funktionen \(f\) und \(g\) die gleiche Steigung.
Überprüfen, ob \(f(x_{1}) = g(x_{1})\) bzw. \(f(x_{2}) = g(x_{2})\) gilt:
\[f(x) = \frac{4}{x^{2}}\]
\[g(x) = -\frac{1}{4}x^{2} + 2\]
\[f(x_{1}) = f(-2) = \frac{4}{(-2)^{2}} = 1\]
\[g(x_{1}) = g(-2) = -\frac{1}{4} \cdot (-2)^{2} + 2 = 1\]
\[\Longrightarrow \quad f(x_{1}) = g(x_{1})\]
\[f(x_{2}) = f(2) = \frac{4}{2^{2}} = 1\]
\[g(x_{2}) = g(2) = -\frac{1}{4} \cdot 2^{2} + 2 = 1\]
\[\Longrightarrow \quad f(x_{2}) = g(x_{2})\]
Schlussfolgerung:
Die Graphen \(G_{f}\) und \(G_{g}\) der Funktionen \(f\) und \(g\) berühren sich in den Punkten \((-2|1)\) und \((2|1)\).
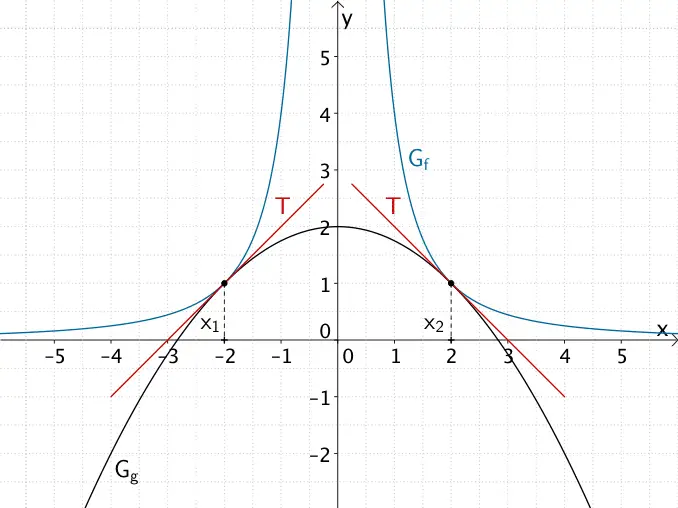
Die Graphen \(G_{f}\) und \(G_{g}\) der Funktionen \(f \colon x \mapsto \dfrac{4}{x^{2}}\) und \(g \colon x \mapsto -\dfrac{1}{4}x^{2} + 2\) besitzen in den Berührpunkten \((-2|1)\) und \((2|1)\) jeweils eine gemeinsame Tangente \(T\).
Schnittwinkel zweier Funktionsgraphen
Schneiden sich die Graphen \(G_{f}\) und \(G_{g}\) zweier Funktionen \(f\) und \(g\) an einer Stelle \(x_{0}\) in einem Schnittpunkt \(S\), so wird der spitze Winkel, unter dem sich die Tangente \(T_{f}\) im Punkt \(S\) an \(G_{f}\) und die Tangente \(T_{g}\) im Punkt \(S\) an \(G_{g}\) schneiden, als Schnittwinkel \(\varphi\) der Funktionsgraphen bezeichnet.
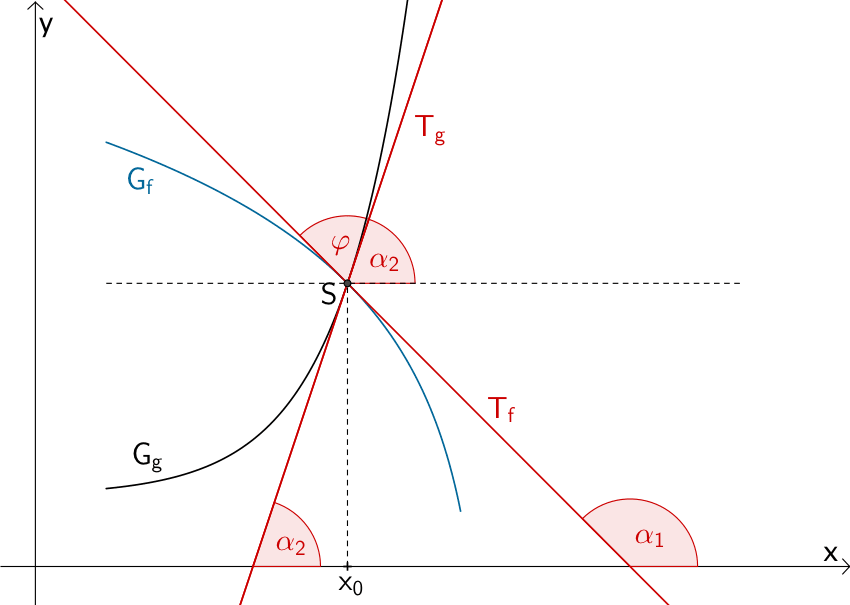
Schnittwinkel \(\varphi\) zweier sich im Schnittpunkt \(S\) schneidenden Graphen der Funktionen \(f\) und \(g\)
Der Schnittwinkel \(\varphi\) lässt sich mithilfe der Steigungen \(m_{T_{f}}\) und \(m_{T_{g}}\) der Tangenten \(T_{f}\) und \(T_{g}\) bestimmen, indem der Zusammenhang zwischen den Tangentensteigungen und den Steigungswinkeln der Tangenten betrachtet wird.
Der Steigungswinkel einer Geraden ist der in mathematisch positivem Sinn (gegen den Uhrzeigersinn) gemessenen Winkel, den die Gerade mit der positiven \(x\)-Achse einschließt.
Für den Steigungswinkel \(\alpha\) einer Geraden mit der Steigung \(m\) gilt (vgl. Abiturskript - 1.1.1 Lineare Funktion, Steigung und Steigungswinkel einer Geraden):
\[\tan{\alpha} = m; \enspace \alpha \neq 90^{\circ}\]
Für die Steigungswinkel \(\alpha_{1}\) und \(\alpha_{2}\) der Tangenten \(T_{f}\) und \(T_{g}\) mit den Steigungen \(m_{T_{f}}\) und \(m_{T_{g}}\) gilt analog:
\[\tan{\alpha_{1}} = m_{T_{f}}\]
\[\tan{\alpha_{2}} = m_{T_{g}}\]
Da die erste Ableitung der Funktionen \(f\) und \(g\) an der Stelle \(x_{0}\) des Schnittpunkts \(S\) die Steigung der Tangenten \(T_{f}\) und \(T_{g}\) an der Stelle \(x_{0}\) beschreibt, folgt (vgl. Abiturskript - 1.5.1 Die Ableitung, Tangentensteigung):
\[\tan{\alpha_{1}} = m_{T_{f}} = f'(x_{0})\]
\[\tan{\alpha_{2}} = m_{T_{g}} = g'(x_{0})\]
Die positive Differenz der Steigungswinkel \(\alpha_{1}\) und \(\alpha_{2}\) der Tangenten \(T_{f}\) und \(T_{g}\) ergibt einen von zwei möglichen Winkeln, unter dem sich die Tangenten schneiden. Ergibt die Differenz einen stumpfen Winkel zwischen 90° und 180°, so ist der Ergänzungswinkel zu 180° der gesuchte (spitze) Schnittwinkel der Tangenten bzw. der Funktionsgraphen.
\[0^{\circ} < \vert \alpha_{1} - \alpha_{2} \vert \leq 90^{\circ} \quad \Longrightarrow \quad \varphi = \vert \alpha_{1} - \alpha_{2}\vert\]
\[90^{\circ} < \vert \alpha_{1} - \alpha_{2} \vert < 180^{\circ} \quad \Longrightarrow \quad \varphi = 180^{\circ} - \vert \alpha_{1} - \alpha_{2}\vert\]
{zen-hand-o-right}Anmerkung:{/zen-hand-o-right}
Der Betrag der Differenz der Schnittwinkel ist nur dann zu berücksichtigen, wenn nicht darauf geachtet wird, welcher der Steigungswinkel größer ist. Eine positive Tangentensteigung entspricht einem Steigungswinkel \(0^{\circ} < \alpha < 90^{\circ}\) und eine negative Steigung entspricht einem Steigungswinkel \(90^{\circ} < \alpha < 180^{\circ}\).
{zen-exclamation-triangle}Bitte beachten:{/zen-exclamation-triangle}
Der Tangens ist am Einheitskreis für Winkel \(-90^{\circ} < \alpha < +90^{\circ}\) definiert. Deshalb gibt der Taschenrechner im Falle einer negativen Tangentensteigung und einem zugehörigen stumpfen Steigungswinkel \(90^{\circ} < \alpha < 180^{\circ}\) mit der Inversfunktion \(\tan^{-1}\) den Winkel, den die Tangente mit der \(x\)-Achse einschließt, in mathematisch negativem Sinn (im Uhrzeigersinn) aus. Um den stumpfen Steigungswinkel in mathematisch positivem Sinn (gegen den Uhrezeigersinn) zu erhalten, addiert man zum Ergebnis 180° (vgl. Abbildung, Steigungswinkel \(\alpha_{1}\) der Tangente \(T_{f}\)).
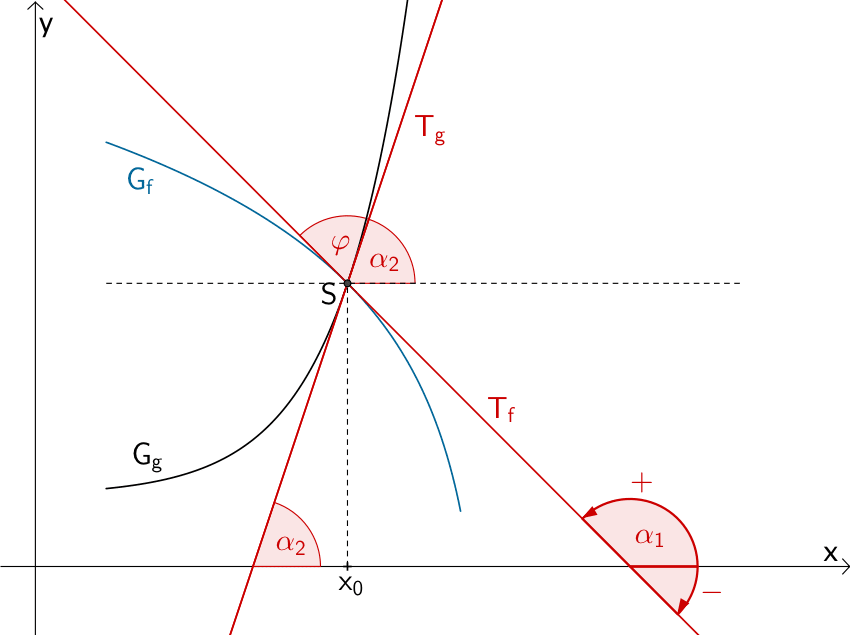
Veranschaulichung: Bestimmung des stumpfen Steigungswinkels \(\alpha_{1}\) im Falle der negativen Tangentensteigung von \(T_{f}\)
Spezialfall - Othogonalität zweier Funktionsgraphen
Für die Steigungen \(m_{1}\) und \(m_{2}\) zweier zueinander senkrechter Geraden gilt: \(m_{1} \cdot m_{2} = -1 \enspace \Leftrightarrow \enspace m_{1} = -\dfrac{1}{m_{2}}\) (vgl. Abiturskript - 1.1.1 Lineare Funktion, Steigung einer Geraden).
Folglich gilt an einer Schnittstelle \(x_{0}\) zweier sich senkrecht zueinander schneidenden Funktionsgraphen \(G_{f}\) und \(G_{g}\):
\[\begin{align*} m_{T_{f}} &= -\frac{1}{m_{T_{g}}} \\[0.8em] f'(x_{0}) &= -\frac{1}{g'(x_{0})} \end{align*}\]
Schnittwinkelformel
Unter Anwendung eines nicht abiturrelevanten Additionstheorems (für den Tangens der Differenz zweier Winkel) lässt sich folgende Formel für die Bestimmung des Schnittwinkels \(\varphi\) zweier sich an einer Stelle \(x_{0}\) schneidenden Funktionsgraphen \(G_{f}\) und \(G_{g}\) angeben:
\[\tan{\varphi} = \left| \frac{m_{T_{f}} - m_{T_{g}}}{1 + m_{T_{f}} \cdot m_{T_{g}}} \right| = \left| \frac{f'(x_{0}) - g'(x_{0})}{1 + f'(x_{0}) \cdot g'(x_{0})} \right|\]
Vorgehensweise - Schnittwinkel zwischen zwei Funktionsgraphen
In einem ersten Schritt wird die Schnittstelle \(x_{0}\) der Graphen zweier Funktionen \(f\) und \(g\) bestimmt. Hierfür werden die Funktionsterme \(f(x)\) und \(g(x)\) gleichgesetzt. Jede Lösung der Gleichung ist eine mögliche Schnittstelle \(x_{0}\). Die Möglichkeit eines Berührpunkts muss ggf. ausgeschlossen werden (vgl. 1.5.9 Seite 3 - Berührpunkt zweier Funktionsgraphen).
\[f(f) = g(x) \quad \Longrightarrow \quad x_{0}\]
Anschließend wird mithilfe der Steigungswinkel der Tangenten \(T_{f}\) und \(T_{g}\) an der Schnittstelle \(x_{0}\) oder mithilfe der Schnittwinkelformel der Schnittwinkel \(\varphi\) der Graphen \(G_{f}\) und \(G_{g}\) bestimmt.
Steigungswinkel:
\[\tan{\alpha_{1}} = f'(x_{0}) \quad \Longrightarrow \quad \alpha_{1}\]
\[\tan{\alpha_{2}} = g'(x_{0}) \quad \Longrightarrow \quad \alpha_{2}\]
\[\varphi = \vert \alpha_{1} - \alpha_{2} \vert\]
bzw.
\[\varphi = 180^{\circ} - \vert \alpha_{1} - \alpha_{2} \vert \]
Schnittwinkelformel:
\[\tan{\varphi} = \left| \frac{f'(x_{0}) - g'(x_{0})}{1 + f'(x_{0}) \cdot g'(x_{0})} \right|\]
\[\Longrightarrow \quad \varphi\]
Beispiel:
Gegeben seien die in \(\mathbb R\) definierten Funktionen \(f \colon x \mapsto \dfrac{1}{4}x^{4} - \dfrac{1}{2}x^{2} - \dfrac{1}{2}\) und \(g \colon x \mapsto \dfrac{1}{4}x^{2} + \dfrac{1}{2}\). Untersuchen Sie die Graphen der Funktionen \(f\) und \(g\) auf Schnittstellen und berechnen Sie die Schnittwinkel der Funktionsgraphen an den Schnittstellen.
\[f(x) = \frac{1}{4}x^{4} - \frac{1}{2}x^{2} - \frac{1}{2}; \: D_{f} = \mathbb R\]
\[g(x) = \frac{1}{4}x^{2} + \frac{1}{2}; \; D_{g} = \mathbb R\]
Schnittstellen der Graphen der Funktionen \(f\) und \(g\)
Für die Berechnung der Schnittstellen werden die Funktionsterme \(f(x)\) und \(g(x)\) gleichgesetzt.
\[\begin{align*} f(x) &= g(x) \\[0.8em] \frac{1}{4}x^{4} - \frac{1}{2}x^{2} - \frac{1}{2} &= \frac{1}{4}x^{2} + \frac{1}{2} & &| -\frac{1}{4}x^{2} - \frac{1}{2} \\[0.8em] \frac{1}{4}x^{4} -\frac{3}{4}x^{2} - 1 &= 0 \end{align*}\]
Die Gleichung kann durch die Substitution \(u = x^{2}\) mit \(u > 0\) in eine quadratische Gleichung umgewandelt werden. Diese lässt sich mithilfe der Lösungsformel für quadratische Gleichungen lösen (vgl. Abiturskript - 1.1.2 Quadratische Funktion, Lösungsformel für quadratische Gleichungen, vgl. Merkhilfe). Die Lösungen der Rücksubstitution \(x^{2} = u\) ergeben die gesuchten Schnittstellen.
Durch die Substitution können sich Scheinlösungen ergeben, die mit \(u > 0\) ausgeschlossen werden können.
Substitution \(u = x^{2}\):
\[\begin{align*}\frac{1}{4}x^{4} -\frac{3}{4}x^{2} - 1 &= 0 & &| \; a^{m \cdot n} = \left( a^{m} \right)^{n} \\[0.8em] \frac{1}{4}\left(x^{2}\right)^{2} - \frac{1}{2}x^{2} - 1 &= 0 & &| \: u = x^{2}; \; u > 0 \\[0.8em] \frac{1}{4}u^{2} - \frac{3}{4}u - 1 &= 0 & &| \cdot 4 \\[0.8em] u^{2} - 3u - 4 &= 0\end{align*}\]
Lösungsformel für quadratische Gleichungen anwenden:
\[\begin{align*} u_{1,2} &= \frac{3 \pm \sqrt{(-3)^{2} - 4 \cdot 1 \cdot (-4)}}{2 \cdot 1} \\[0.8em] &= \frac{3 \pm \sqrt{9 + 16}}{2} \\[0.8em] &= \frac{3 \pm 5}{2} \end{align*}\]
\[\left( u_{1} = \frac{3 - 5}{2} = -1 \right)\]
\[u_{2} = \frac{3 + 5}{2} = 4\]
Rücksubstitution \(x^{2} = u_{2}\):
\[\begin{align*} x^{2} &= 4 & &| \; \sqrt{\quad} \\[0.8em] x_{1,2} &= \pm 2 \end{align*}\]
Die Graphen der Funktionen \(f\) und \(g\) schneiden sich an den Stellen \(x_{1} = -2\) und \(x_{2} = 2\).
Schnittwinkel der Graphen der Funktionen \(f\) und \(g\)
1. Möglichkeit: Steigungswinkel der Tangenten berechnen
Erste Ableitungen \(f'\) und \(g'\) bilden:
Die Ableitungen der Funktionsterme \(f(x)\) und \(g(x)\) können mithilfe der Faktorregel, der Summenregel und der Ableitung einer Potenzfunktion erfolgen (vgl. Abiturskript - 1.5.2 Ableitungsregeln).
\[f(x) = \frac{1}{4}x^{4} - \frac{1}{2}x^{2} - \frac{1}{2}\]
\[f'(x) = \frac{1}{4} \cdot 4 \cdot x^{3} - \frac{1}{2} \cdot 2 \cdot x - 0 = x^{3} - x\]
\[g(x) = \frac{1}{4}x^{2} + \frac{1}{2}\]
\[g'(x) = \frac{1}{4} \cdot 2 \cdot x + 0 = \frac{1}{2}x\]
Schnittwinkel \(\varphi_{1}\) an der Schnittstelle \(x_{1} = -2\):
Es sei \(\alpha_{1}\) der Steigungswinkel der Tangente \(T_{f}\) an den Graphen der Funktion \(f\) und \(\alpha_{2}\) der Steigungswinkel der Tangente \(T_{g}\) an den Graphen der Funktion \(g\), jeweils an der Schnittstelle \(x_{1} = -2\).
Steigungswinkel \(\alpha_{1}\):
\[\begin{align*} \tan{\alpha_{1}} &= f'(-2) \\[0.8em] &= (-2)^{3} - (-2) \\[0.8em] &= -8 + 2 \\[0.8em] &= -6 & &| \; \text{TR:} \; \tan^{-1}(\dots) \end{align*}\]
\[\tan^{-1}(-6) \approx -80{,}5^{\circ}\]
\[\Longrightarrow \quad \alpha_{1} = -80{,}5^{\circ} + 180^{\circ} = 99{,}5^{\circ}\]
Steigungswinkel \(\alpha_{2}\):
\[\begin{align*} \tan{\alpha_{2}} &= g'(-2) \\[0.8em] &= \frac{1}{2} \cdot (-2) \\[0.8em] &= -1 & &| \; \text{TR:} \; \tan^{-1}(\dots) \end{align*}\]
\[\tan^{-1}(-1) = -45^{\circ}\]
\[\Longrightarrow \quad \alpha_{2} = -45^{\circ} + 180^{\circ} = 135^{\circ} \]
Schnittwinkel \(\varphi_{1}\):
\[\varphi_{1} = \vert \alpha_{1} - \alpha_{2} \vert = \vert 99{,}5^{\circ} - 135^{\circ} \vert = \vert -35{,}5^{\circ} \vert = 35{,}5^{\circ}\]
Schnittwinkel \(\varphi_{2}\) an der Schnittstelle \(x_{2} = 2\):
Es sei \(\alpha_{3}\) der Steigungswinkel der Tangente \(T_{f}\) an den Graphen der Funktion \(f\) und \(\alpha_{4}\) der Steigungswinkel der Tangente \(T_{g}\) an den Graphen der Funktion \(g\), jeweils an der Schnittstelle \(x_{2} = 2\).
Steigungswinkel \(\alpha_{3}\):
\[\begin{align*} \tan{\alpha_{3}} &= f'(2) \\[0.8em] &= 2^{3} - 2 \\[0.8em] &= 8 - 2 \\[0.8em] &= 6 & &| \; \text{TR:} \; \tan^{-1}(\dots) \end{align*}\]
\[\tan^{-1}(6) \approx 80{,}5^{\circ}\]
\[\Longrightarrow \quad \alpha_{3} = 80{,}5^{\circ}\]
Steigungswinkel \(\alpha_{4}\):
\[\begin{align*} \tan{\alpha_{4}} &= g'(2) \\[0.8em] &= \frac{1}{2} \cdot 2 \\[0.8em] &= 1 & &| \; \text{TR:} \; \tan^{-1}(\dots) \end{align*}\]
\[\tan^{-1}(1) = 45^{\circ}\]
\[\Longrightarrow \quad \alpha_{4} = 45^{\circ}\]
Schnittwinkel \(\varphi_{2}\):
\[\varphi_{2} = \vert \alpha_{3} - \alpha_{4} \vert = \vert 80{,}5^{\circ} - 45^{\circ} \vert = 35{,}5^{\circ}\]
Die Graphen der Funktionen \(f\) und \(g\) schneiden sich an den Schnittstellen \(x_{1} = -2\) und \(x_{2} = 2\) jeweils in einem Winkel von 45°.
{zen-hand-o-right}Anmerkung:{/zen-hand-o-right}
Beachtet man, dass die Graphen der Funktionen \(f\) und \(g\) achsensymmetrisch zur \(y\)-Achse sind, da deren Funktionsterme ausschließlich gerade Potenzen enthalten, verkürzt sich der Lösungsweg entsprechend (vgl. Abiturskript - 1.1.3 Ganzrationale Funktion, Symmetrieverhalten).
2. Möglichkeit: Schnittwinkelformel anwenden
Schnittwinkel \(\varphi_{1}\):
\[x_{1} = -2; \enspace f'(-2) = -6; \enspace g'(-2) = -1\]
\[\begin{align*}\tan{\varphi_{1}} &= \left| \frac{f'(-2) - g'(-2)}{1 + f'(-2) \cdot g'(-2)} \right| \\[0.8em] &= \left| \frac{-6 - (-1)}{1 + (-6) \cdot (-1)} \right| \\[0.8em] &= \left| \frac{-5}{7} \right| \\[0.8em] &= \frac{5}{7} & &| \; \text{TR:} \; \tan^{-1}(\dots) \end{align*}\]
\[\tan^{-1}\left( \frac{5}{7} \right) \approx 35{,}5^{\circ}\]
\[\Longrightarrow \quad \varphi_{1} \approx 35{,}5^{\circ}\]
Schnittwinkel \(\varphi_{2}\):
\[x_{1} = 2; \enspace f'(2) = 6; \enspace g'(2) = 1\]
\[\begin{align*}\tan{\varphi_{2}} &= \left| \frac{f'(2) - g'(2)}{1 + f'(2) \cdot g'(2)} \right| \\[0.8em] &= \left| \frac{6 - 1}{1 + 6 \cdot 1} \right| \\[0.8em] &= \left| \frac{5}{7} \right| \\[0.8em] &= \frac{5}{7} & &| \; \text{TR:} \; \tan^{-1}(\dots) \end{align*}\]
\[\tan^{-1}\left( \frac{5}{7} \right) \approx 35{,}5^{\circ}\]
\[\Longrightarrow \quad \varphi_{2} \approx 35{,}5^{\circ}\]
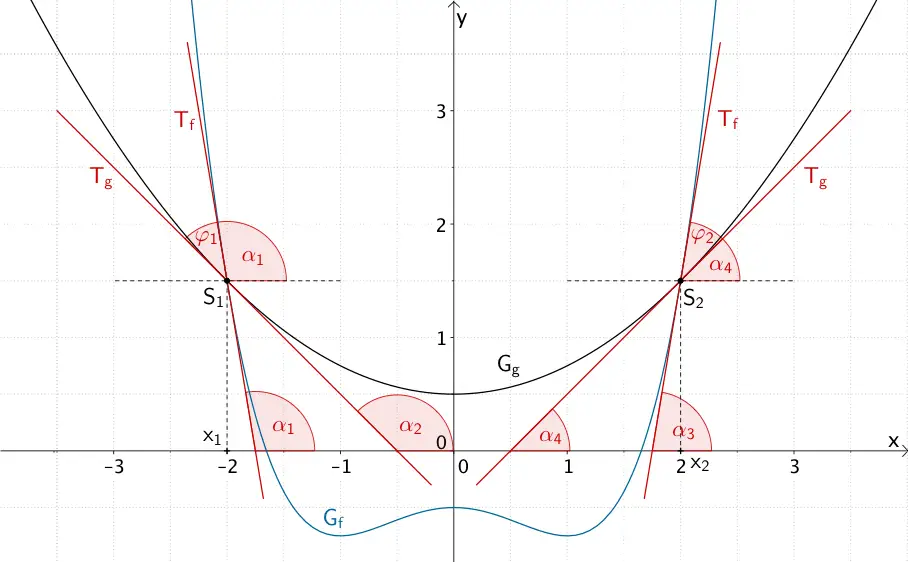
Schnittstellen \(x_{1} = -2\) und \(x_{2} = 2\) sowie Schnittwinkel \(\varphi_{1} = \varphi_{2} \approx 35{,}5^{\circ}\) der Graphen \(G_{f}\) und \(G_{g}\) der Funktionen \(f \colon x \mapsto \dfrac{1}{4}x^{4} - \dfrac{1}{2}x^{2} - \dfrac{1}{2}\) und \(g \colon x \mapsto \dfrac{1}{4}x^{2} + \dfrac{1}{2}\).
Beispielaufgabe
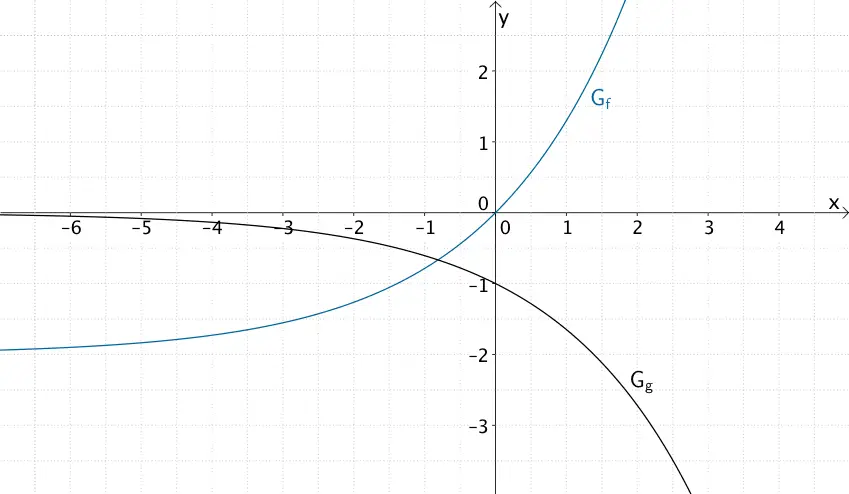
Die Abbildung zeigt die Graphen \(G_{f}\) und \(G_{g}\) der in \(\mathbb R\) definierten Funktionen \(f \colon x \mapsto 2e^{0{,}5x} - 2\) und \(g \colon x \mapsto -e^{0{,}5x}\).
a) Zeigen Sie rechnerisch, dass es keine Stelle \(x \in \mathbb R\) gibt, an der die Graphen \(G_{f}\) und \(G_{g}\) die gleiche Steigung besitzen.
b) Ermitteln Sie diejenige Stelle \(x_{0}\), an der die Tangenten an die Graphen \(G_{f}\) und \(G_{g}\) senkrecht zueinander sind.
c) Die Graphen \(G_{f}\) und \(G_{g}\) schneiden sich im Punkt \(S\). Berechnen Sie den Schnittwinkel der Graphen in diesem Punkt.
\[f(x) = 2e^{0{,}5x} - 2; \; D_{f} = \mathbb R\]
\[g(x) = -e^{0{,}5x}; \; D_{g} = \mathbb R\]
a) Nachweis, dass es keine Stelle gleicher Steigung von \(G_{f}\) und \(G_{g}\) gibt
Unter der Steigung eines Funktionsgraphen versteht man die Steigung der Tangente an den Graphen der Funktion an einer betrachteten Stelle. Die Steigung einer Tangente an den Graphen einer Funktion wird durch die Ableitungsfunktion beschrieben (vgl. Abiturskript - 1.5.1 Die Ableitung, Tangentensteigung). Folglich ist zu zeigen, dass die Gleichung \(f'(x) = g'(x)\) in \(\mathbb R\) keine Lösung hat.
Für eine alternative Argumentation bietet sich das Monotoniekriterium an (vgl. Abiturskript - 1.5.3 Monotonieverhalten, Extrem- und Terrassenpunkte, vgl. Merkhilfe).
Erste Ableitung \(f'\) und \(g'\) bilden:
Die Ableitungen der Funktionsterme \(f(x)\) und \(g(x)\) können mithilfe der Faktorregel, der Summenregel, der Ableitung der Natürlichen Exponentialfunktion und der Kettenregel erfolgen (vgl. Abiturskript - 1.5.2 Ableitungsregeln).
\[f(x) = 2e^{0{,}5x} - 2\]
\[f'(x) = 2 \cdot e^{0{,}5x} \cdot 0{,}5 - 0 = e^{0{,}5x}\]
\[g(x) = -e^{0{,}5x}\]
\[g'(x) = -e^{0{,}5x} \cdot 0{,}5 = -0{,}5e^{0{,}5x}\]
Nachweisen, dass die Gleichung \(f'(x) = g'(x)\) in \(\mathbb R\) keine Lösung hat:
\[\begin{align*}f'(x) &= g'(x) \\[0.8em] e^{0{,}5x} &= -0{,}5e^{0{,}5x} & &| : e^{0{,}5x} \\[0.8em] 1 &= -0{,}5 \quad (\text{f}) \end{align*}\]
Schlussfolgerung:
Es gibt keine Stelle \(x \in \mathbb R\), an der die Graphen \(G_{f}\) und \(G_{g}\) die gleiche Steigung besitzen.
Alternative mithilfe des Monotoniekriteriums (vgl. Abiturskript - 1.5.3 Monotonieverhalten, Extrem- und Terrassenpunkte, vgl. Merkhilfe):
\[f'(x) = \underbrace{e^{0{,}5x}}_{>\, 0}; \enspace g'(x) = -0{,}5 \cdot \underbrace{e^{0{,}5x}}_{> \, 0}\]
(vgl. Abiturskript - 1.3.1 Eigenschaften und Rechenregeln, Natürliche Exponential- und Logarithmusfunktion)
\(f'(x) > 0\) für alle \(x \in \mathbb R \quad \Longrightarrow \quad G_{f}\) ist in \(\mathbb R\) streng monoton steigend.
\(g'(x) < 0\) für alle \(x \in \mathbb R \quad \Longrightarrow \quad G_{g}\) ist in \(\mathbb R\) streng monoton fallend.
Schlussfolgerung:
Es gibt keine Stelle \(x \in \mathbb R\), an der die Graphen \(G_{f}\) und \(G_{g}\) die gleiche Steigung besitzen.
b) Stelle \(x_{0}\), an der die Tangenten an \(G_{f}\) und \(G_{g}\) senkrecht zueinander sind
An der gesuchten Stelle \(x_{0}\) muss die Bedingung \(f'(x_{0}) = -\dfrac{1}{g'(x_{0})}\) gelten (vgl. 1.5.9 Seite 3 - Stelle mit orthogonalen Tangenten zweier Funktionsgraphen).
\[f'(x) = e^{0{,}5x}; \enspace g'(x) = -0{,}5e^{0{,}5x}\]
\[\begin{align*} f'(x) &= -\frac{1}{g'(x)} \\[0.8em] e^{0{,}5x} &= -\frac{1}{-0{,}5e^{0{,}5x}} \\[0.8em] e^{0{,}5x} &= \frac{2}{e^{0{,}5x}} & &| \cdot e^{0{,}5x} \\[0.8em] e^{0{,}5x} \cdot e^{0{,}5x} &= 2 & &| \; a^{m} \cdot a^{n} = a^{m + n} \\[0.8em] e^{x} &= 2 & &| \: \ln(\dots) \; \text{Logarithmieren} \\[0.8em] \ln\left( e^{x} \right) &= \ln{2} & &| \; \ln\left( e^{x} \right) = x \enspace \left( \text{allg.:} \; \log_{a}\left( a^{x} \right) = x\right) \\[0.8em] x &= \ln{2} \end{align*}\]
An der Stelle \(x_{0} = \ln{2}\) sind die Tangente \(T_{f}\) an den Graphen der Funktion \(f\) und die Tangente \(T_{g}\) an den Graphen der Funktion \(g\) zueinander senkrecht (orthogonal).
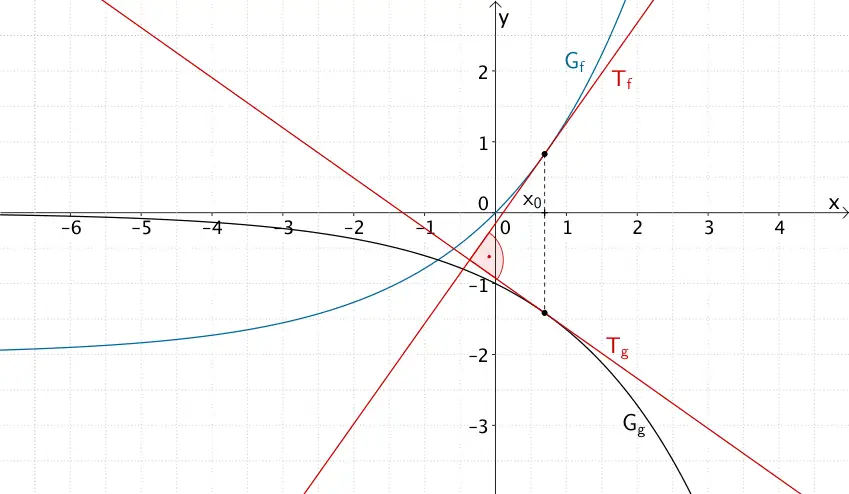
Stelle \(x_{0} = \ln{2}\), an der die Tangente \(T_{f}\) an den Graphen der Funktion \(f \colon x \mapsto 2e^{0{,}5} - 2\) und die Tangente \(T_{g}\) an den Graphen der Funktion \(g \colon x \mapsto -e^{0{,}5x}\) zueinander senkrecht sind.
c) Schnittwinkel der Graphen \(G_{f}\) und \(G_{g}\) im Schnittpunkt \(S\)
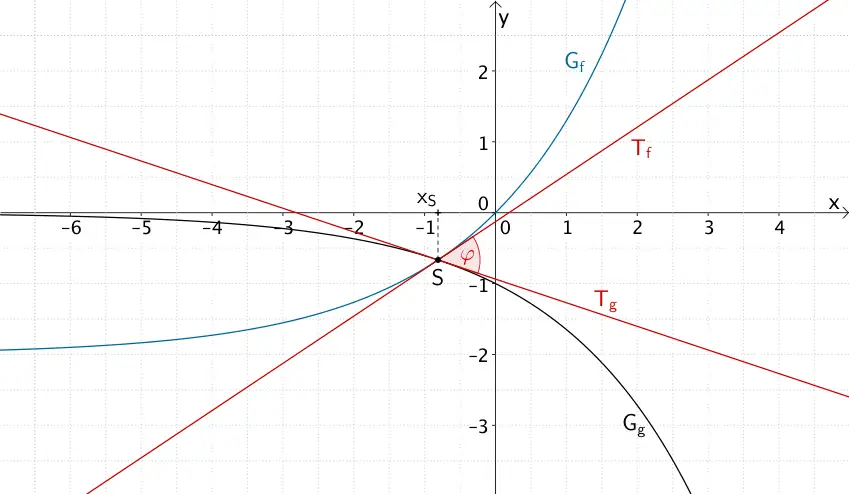
Schnittwinkel \(\varphi\) der Graphen der Funktionen \(f\) und \(G\) im Schnittpunkt \(S\)
Der Schnittwinkel \(\varphi\) der Graphen der Funktionen \(f\) und \(g\) im Schnittpunkt \(S\) entspricht dem spitzen Winkel, den die Tangente \(T_{f}\) an den Graphen der Funktion \(f\) und die Tangente \(T_{g}\) an den Graphen der Funktion \(G\) an der Schnittstelle \(x_{S}\) einschließen.
Schnittstelle \(x_{S}\) von \(G_{f}\) und \(G_{g}\)
Für die Berechnung der Schnittstelle \(x_{S}\) der Graphen der Funktionen \(f\) und \(g\) werden die Funktionsterme \(f(x)\) und \(g(x)\) gleichgesetzt und die Gleichung nach \(x\) aufgelöst.
\[f(x) = 2e^{0{,}5x} - 2; \; D_{f} = \mathbb R\]
\[g(x) = -e^{0{,}5x}; \; D_{g} = \mathbb R\]
\[\begin{align*} f(x) &= g(x) \\[0.8em] 2e^{0{,}5x} - 2 &= -e^{0{,}5x} \end{align*}\]
Die Exponentialgleichung lässt sich mithilfe elementarer Umformungen und einer sich anschließenden Logarithmierung lösen (vgl. Abiturskript - 1.3.3 Exponential- und Logarithmusgleichungen).
\[\begin{align*} 2e^{0{,}5x} - 2 &= -e^{0{,}5x} & &| + e^{0{,}5x} + 2 \\[0.8em] 3e^{0{,}5x} &= 2 & &| : 3 \\[0.8em] e^{0{,}5x} &= \frac{2}{3} & &| \; \ln{(\dots)} \; \text{Logarithmieren} \\[0.8em] \ln \left( e^{0{,}5x} \right) &= \ln\left( \frac{2}{3} \right) & &| \; \ln\left( e^{x} \right) = x \enspace \left( \text{allg.:} \; \log_{a}\left( a^{x} \right) = x\right) \\[0.8em] 0{,}5x &= \ln\left( \frac{2}{3} \right) & &| \cdot 2 \\[0.8em] x &= 2\ln\left( \frac{2}{3} \right) \end{align*}\]
Die Graphen der Funktionen \(f\) und \(g\) schneiden sich an der Stelle \(x_{S} = 2\ln\left( \frac{2}{3} \right)\).
Schnittwinkel der Graphen der Funktionen \(f\) und \(g\) im Schnittpunkt \(S\)
(vgl. 1.5.9 Seite 4 - Schnittwinkel zweier Funktionsgraphen)
1. Möglichkeit: Steigungswinkel der Tangenten berechnen
Es sei \(\alpha_{1}\) der Steigungswinkel der Tangente \(T_{f}\) an den Graphen der Funktion \(f\) und \(\alpha_{2}\) der Steigungswinkel der Tangente \(T_{g}\) an den Graphen der Funktion \(g\), jeweils an der Schnittstelle \(x_{S} = 2\ln\left( \frac{2}{3} \right)\).
\(f'(x) = e^{0{,}5x}; \enspace g'(x) = -0{,}5e^{0{,}5x}\) (vgl. Teilaufgabe a)
Steigungswinkel \(\alpha_{1}\):
\[\begin{align*} \tan{\alpha_{1}} &= f'\left( 2\ln\left( \frac{2}{3} \right) \right) \\[0.8em] &= e^{0{,}5 \cdot 2 \ln\left( \frac{2}{3} \right)} \\[0.8em] &= e^{\ln\left( \frac{2}{3} \right)} & &| \; e^{\ln{x}} = x \enspace \left( \text{allg.:} \; a^{\log_{a}{x}} = x \right) \\[0.8em] &= \frac{2}{3} & &| \; \text{TR:} \; \tan^{-1}{(\dots)} \end{align*}\]
\[\tan^{-1}{\left( \frac{2}{3} \right)} \approx 33{,}7^{\circ}\]
\[\Longrightarrow \quad \alpha_{1} = 33{,}7^{\circ}\]
Steigungswinkel \(\alpha_{2}\):
\[\begin{align*} \tan{\alpha_{2}} &= g'\left( 2\ln\left( \frac{2}{3} \right) \right) \\[0.8em] &= -0{,}5e^{0{,}5 \cdot 2 \ln\left( \frac{2}{3} \right)} \\[0.8em] &= -0{,}5e^{\ln\left( \frac{2}{3} \right)} & &| \; e^{\ln{x}} = x \enspace \left( \text{allg.:} \; a^{\log_{a}{x}} = x \right) \\[0.8em] &= (-0{,}5) \cdot \frac{2}{3} \\[0.8em] &= -\frac{1}{3} & &| \; \text{TR:} \; \tan^{-1}{(\dots)} \end{align*}\]
\[\tan^{-1}{\left( -\frac{1}{3} \right)} \approx -18{,}4^{\circ}\]
\[\Longrightarrow \quad \alpha_{1} = -18{,}4^{\circ} + 180^{\circ} = 161{,}1^{\circ}\]
Schnittwinkel \(\varphi\):
\[\vert \alpha_{1} - \alpha_{2} \vert = \vert 33{,}7^{\circ} - 161{,}1^{\circ} \vert = \vert -127{,}9^{\circ} \vert = 127{,}9^{\circ}\]
In diesem Fall errechnet die positive Differenz der Steigungswinkel \(\alpha_{1}\) und \(\alpha_{2}\) zunächst den stumpfen Winkel, den Die Tangenten \(T_{f}\) und \(T_{g}\) an der Schnittstelle \(x_{S}\) einschließen. Der (spitze) Schnittwinkel \(\varphi\) ist der Ergänzungswinkel zu \(180^{\circ}\).
\[\varphi = 180^{\circ} - \vert \alpha_{1} - \alpha_{2} \vert = 180^{\circ} - 127{,}9^{\circ} = 52{,}1^{\circ} \]
Die Graphen der Funktionen \(f\) und \(g\) schneiden sich an der Schnittstelle \(x_{S} = 2\ln\left( \frac{2}{3} \right)\) in einem Winkel von 52,1°.
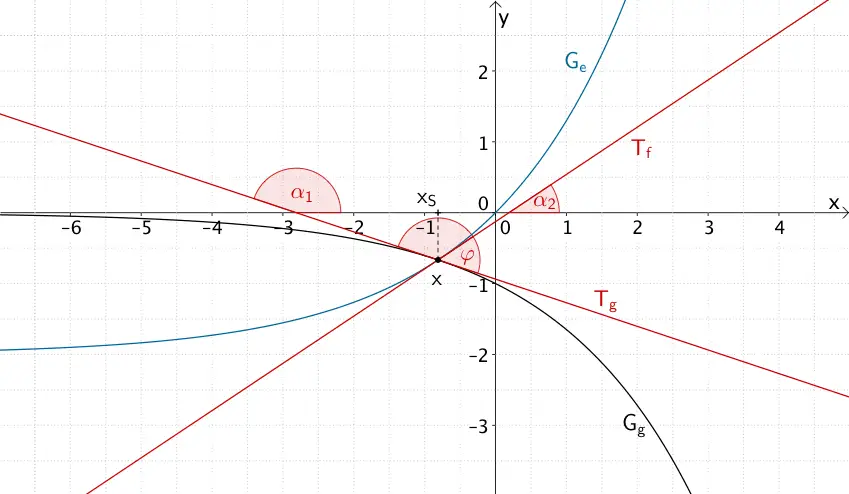
Schnittwinkel \(\varphi\) der Graphen \(G_{f}\) und \(G_{g}\) der Funktionen \(f \colon x \mapsto 2e^{0{,}5x} - 2\) und \(g \colon x \mapsto -e^{0{,}5x}\) im Schnittpunkt \(S\) sowie Steigungswinkel \(\alpha_{1}\) und \(\alpha_{2}\) der Tangenten \(T_{f}\) und \(T_{g}\) an der Schnittstelle \(x_{S} = 2\ln\left( \frac{2}{3} \right)\)
2. Möglichkeit: Schnittwinkelformel anwenden
\[x_{S} = 2\ln\left( \frac{2}{3} \right); \enspace f'\left( 2\ln\left( \frac{2}{3} \right)\right) = \frac{2}{3}; \enspace g'\left( 2\ln\left( \frac{2}{3} \right)\right) = -\frac{1}{3}\]
\[\begin{align*}\tan{\varphi} &= \left|\frac{ f'\left( 2\ln\left( \frac{2}{3} \right)\right) - g'\left( 2\ln\left( \frac{2}{3} \right)\right)}{1 + f'\left( 2\ln\left( \frac{2}{3} \right)\right) \cdot g'\left( 2\ln\left( \frac{2}{3} \right)\right)} \right| \\[0.8em] &= \left| \frac{\frac{2}{3} - \left(-\frac{1}{3}\right)}{1 + \frac{2}{3} \cdot \left(-\frac{1}{3}\right)} \right| \\[0.8em] &= \left| \frac{1}{1 - \frac{2}{9}} \right| \\[0.8em] &= \frac{1}{\frac{7}{9}} \\[0.8em] &= \frac{9}{7} & &| \; \text{TR:} \; \tan^{-1}(\dots) \end{align*}\]
\[\tan^{-1}\left( \frac{9}{7} \right) \approx 52{,}1^{\circ}\]
\[\Longrightarrow \quad \varphi \approx 52{,}1^{\circ}\]
Die Graphen der Funktionen \(f\) und \(g\) schneiden sich an der Schnittstelle \(x_{S} = 2\ln\left( \frac{2}{3} \right)\) in einem Winkel von 52,1°.


