- Details
- Kategorie: Stochastik II
Auf der Strecke München-Tokio bietet eine Fluggesellschaft ihren Passagieren verschiedene Menüs an, darunter ein vegetarisches. Aus Erfahrung weiß man, dass sich im Mittel 10 % der Passagiere für das vegetarische Menü entscheiden. Im Folgenden soll davon ausgegangen werden, dass die Passagiere ihre jeweilige Menüauswahl unabhängig voneinander treffen.
Auf einem Flug nach Tokio sind 200 Passagiere an Bord. Bestimmen Sie die Wahrscheinlichkeit dafür, dass sich mindestens 20 und höchstens 25 Passagiere für das vegetarische Menü entscheiden.
(4 BE)
- Details
- Kategorie: Stochastik II
Auf dem Rückflug nach München ist die Maschine mit 240 Passagieren besetzt.
Berechnen Sie die Wahrscheinlichkeit dafür, dass sich auf dem Rückflug genau 20 Passagiere für das vegetarische Menü entscheiden.
(3 BE)
- Details
- Kategorie: Stochastik II
Tatsächlich entscheiden sich auf dem Rückflug sechs weibliche und vierzehn männliche Reisende für das vegetarische Menü. Ermitteln Sie, wie viele weibliche Reisende unter den Passagieren sind, wenn die Ereignisse "Ein zufällig ausgewählter Passagier ist weiblich." und "Ein zufällig ausgewählter Passagier entscheidet sich für das vegetarische Menü." unabhängig sind.
(4 BE)
- Details
- Kategorie: Stochastik II
Die Fluggesellschaft beabsichtigt , ihren Passagieren neben dem Standardmenü gegen Zuzahlung ein Premiummenü anzubieten, möchte diesen Service jedoch nur dann einrichten, wenn er von mehr als 15 % der Passagiere gewünscht wird. Die Nullhypothese "Höchstens 15 % der Passagiere wünschen das Angebot eines Premiummenüs." soll auf der Basis einer Stichprobe von 200 Passagieren auf einem Signifikanzniveau von 5 % getestet werden.
Bestimmen Sie die zugehörige Entscheidungsregel.
(5 BE)
- Details
- Kategorie: Stochastik II
Die Fluggesellschaft hätte für den Test - bei gleichem Signifikanzniveau - anstelle der Nullhypothese
"Höchstens 15 % der Passagiere wünschen das Angebot eines Premiummenüs."
auch die Nullhypothese
"Mehr als 15 % der Passagiere wünschen das Angebot eines Premiummenüs."
wählen können. Bei der Wahl der Nullhypothese stand für die Fluggesellschaft eine der beiden folgenden Überlegungen im Vordergrund
-
Der irrtümliche Verzicht auf das Angebot des Premiummenüs wäre mit einem Imageverlust verbunden.
-
Das irrtümliche Angebot des Premiummenüs wäre mit einem finaziellen Verlust verbunden.
Entscheiden Sie, welche der beiden Überlegungen für die Fluggesellschaft bei der Wahl der Nullhypothese im Vordergrund stand. Erläutern Sie Ihre Entscheidung.
(3 BE)
- Details
- Kategorie: Stochastik II
Bei einer Routineinspektion wird die Passagierkabine eines zufällig ausgewählten Flugzeugs des Typs X überprüft. Ein Mangel der Beleuchtung sowie ein Mangel der Klimaanlage liegen bei Flugzeugen dieses Typs jeweils mit einer bestimmten Wahrscheinlichkeit vor; diese Wahrscheinlichkeiten können der folgenden Vierfeldertafel entnommen werden.
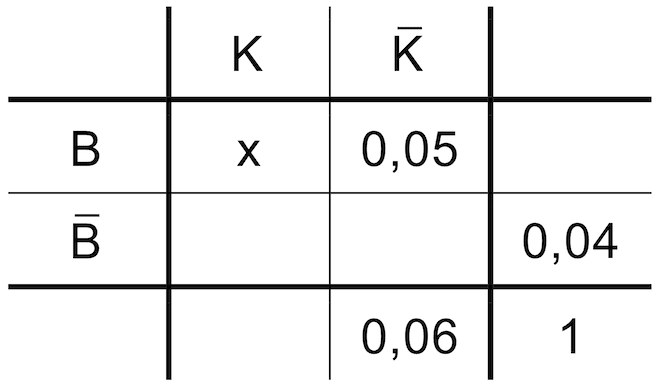
\(B\): Beleuchtung einwandfrei
\(\overline{B}\): Beleuchtung mangelhaft
\(K\): Klimaanlage einwandfrei
\(\overline{K}\): Klimaanlage mangelhaft
Bestimmen Sie den Wert von \(x\) und beschreiben Sie das zugehörige Ereignis in Worten.
(3 BE)
- Details
- Kategorie: Stochastik II
Mit welcher Wahrscheinlichkeit liegt bei dem zufällig ausgewählten Flugzeug des Typs X ein Mangel der Klimaanlage vor, wenn die Beleuchtung nicht einwandfrei funktioniert?
(3 BE)
- Details
- Kategorie: Stochastik II
Bei Flugzeugen eines anderen Typs Y liegt ein Mangel der Klimaanlage mit einer Wahrscheinlichkeit von 4 % vor. Die Wahrscheinlichkeit dafür, dass mindestens einer der beiden Mängel vorliegt, beträgt 5 %. Wenn mindestens einer der beiden Mängel vorliegt, so funktioniert mit einer Wahrscheinlichkeit von 40 % die Beleuchtung nicht einwandfrei. Stellen Sie zu der für Flugzeuge des Typs Y beschriebenen Situation eine vollständig ausgefüllte Vierfeldertafel auf.
(5 BE)

