- Details
- Kategorie: Analysis 1
Gegeben ist die in \(\mathbb R^{+}\) definierte Funktion \(h \colon x \mapsto 3x \cdot (-1 + \ln x)\).
Abbildung 1 zeigt den Graphen \(G_{h}\) von \(h\) im Bereich \(0{,}75 \leq x \leq 4\).
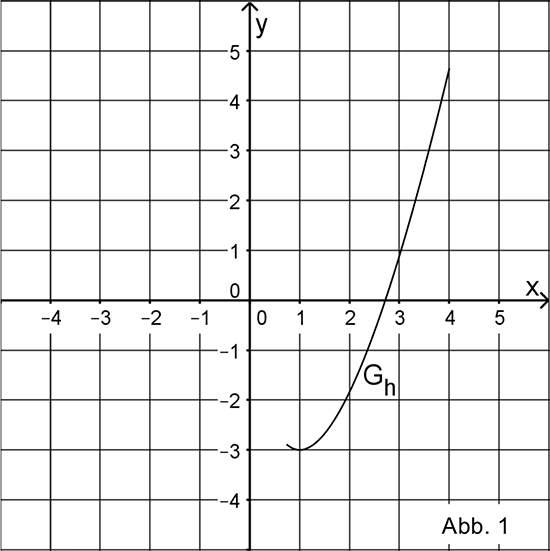
Bestimmen Sie die Gleichung der Tangente an \(G_{h}\) im Punkt \((e|0)\) und berechnen Sie die Größe des Winkels, unter dem diese Tangente die \(x\)-Achse schneidet.
(zur Kontrolle: \(h'(x) = 3 \cdot \ln x\))
(4 BE)
- Details
- Kategorie: Analysis 1
Untersuchen Sie das Monotonieverhalten von \(G_{h}\). Geben Sie den Grenzwert von \(h\) für \(x \to +\infty\) an und begründen Sie, dass \([-3;+\infty[\) die Wertemenge von \(h\) ist.
(4 BE)
- Details
- Kategorie: Analysis 1
Geben Sie für die Funktion \(h\) und deren Ableitungsfunktion \(h'\) jeweils das Verhalten für \(x \to 0\) an und zeichnen Sie \(G_{h}\) im Bereich \(0 < x < 0{,}75\) in Abbildung 1 ein.
(3 BE)
- Details
- Kategorie: Analysis 1
Die Funktion \(h^{*}\colon x \mapsto h(x)\) mit Definitionsmenge \([1;+\infty[\) unterscheidet sich von der Funktion \(h\) nur hinsichtlich der Definitionsmenge. Im Gegensatz zu \(h\) ist die Funktion \(h^{*}\) umkehrbar.
Geben Sie die Definitionsmenge und die Wertemenge der Umkehrfunktion \(h^{*}\) an. Berechnen Sie die Koordinaten des Schnittpunkts \(S\) des Graphen von \(h^{*}\) und der Geraden mit der Gleichung \(y = x\).
(Teilergebnis: \(x\)-Koordinate des Schnittpunkts: \(e^{\frac{4}{3}}\))
(4 BE)
- Details
- Kategorie: Analysis 1
Zeichnen Sie den Graphen der Umkehrfunktion von \(h^{*}\) unter Verwendung der bisherigen Ergebnisse, insbesondere der Lage von Punkt \(S\), in Abbildung 1 ein.
(3 BE)
- Details
- Kategorie: Analysis 1
Schraffieren Sie in Abbildung 1 ein Flächenstück, dessen Inhalt \(A_{0}\) dem Wert des Integrals \(\displaystyle \int_{e}^{x_{S}} (x - h^{*}(x)) dx\) entspricht, wobei \(x_{S}\) die \(x\)-Koordinate von Punkt \(S\) ist. Der Graph von \(h^{*}\), der Graph der Umkehrfunktion von \(h^{*}\) sowie die beiden Koordinatenachsen schließen im ersten Quadranten ein Flächenstück mit Inhalt \(A\) ein. Geben Sie unter Verwendung von \(A_{0}\) einen Term zur Berechnung von \(A\) an.
(4 BE)
- Details
- Kategorie: Analysis 1
Abbildung 2 zeigt den Graphen einer in \([0;16]\) definierten Funktion \(V \colon t \mapsto V(t)\). Sie beschreibt modellhaft das sich durch Zu- und Abfluss ändernde Volumen von Wasser in einem Becken in Abhängigkeit von der Zeit. Dabei bezeichnet \(t\) die seit Beobachtungsbeginn vergangene Zeit in Stunden und \(V(t)\) das Volumen in Kubikmetern.
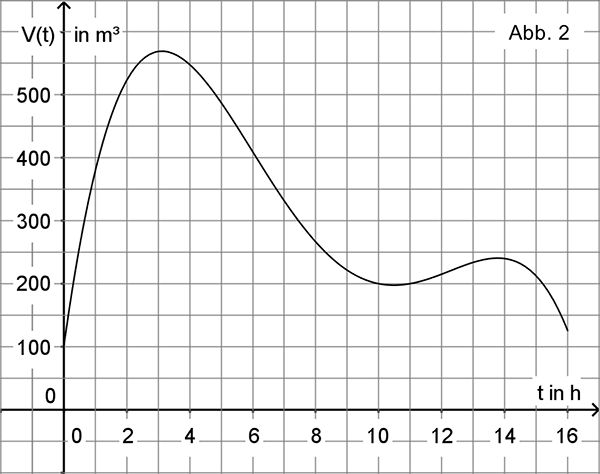
Geben Sie mithilfe von Abbildung 2 jeweils näherungsweise das Volumen des Wassers fünf Stunden nach Beobachtungsbeginn sowie den Zeitraum an, in dem das Volumen mindestens 450 m³ beträgt.
(2 BE)
- Details
- Kategorie: Analysis 1
Bestimmen Sie anhand des Graphen der Funktion \(V\) näherungsweise die momentane Änderungsrate des Wasservolumens zwei Stunden nach Beobachtungsbeginn.
(3 BE)
- Details
- Kategorie: Analysis 1
Erläutern Sie, was es im Sachzusammenhang bedeutet, wenn für ein \(t \in [0;10]\) die Beziehung \(V(t + 6) = V(t) - 350\) gilt. Entscheiden Sie mithilfe von Abbildung 2, ob für \(t = 5\) diese Beziehung gilt, und begründen Sie Ihre Entscheidung.
(3 BE)
- Details
- Kategorie: Analysis 1
In einem anderen Becken ändert sich das Volumen des darin enthaltenen Wassers ebenfalls durch Zu- und Abfluss. Die momentane Änderungsrate des Volumens wird für \(0 \leq t \leq 12\) modellhaft durch die in \(\mathbb R\) definierte Funktion \(g \colon t \mapsto 0{,}4 \cdot (2t^{3} - 39t^{2} + 180t)\) beschrieben. Dabei ist \(t\) die seit Beobachtungsbeginn vergangene Zeit in Stunden und \(g(t)\) die momentane Änderungsrate des Volumens in \(\frac{\sf{m^{3}}}{\sf{h}}\).
Begründen Sie, dass die Funktionswerte von \(g\) für \(0 < t < 7{,}5\) positiv und für \(7{,}5 < t < 12\) negativ sind.
(4 BE)
- Details
- Kategorie: Analysis 1
Erläutern Sie die Bedeutung des Werts des Integrals \(\displaystyle \int_{a}^{b} g(t) dt\) für \(0 \leq a < b \leq 12\) im Sachzusammenhang. Berechnen Sie das Volumen des Wassers, das sich 7,5 Stunden nach Beobachtungsbeginn im Becken befindet, wenn zu Beobachtungsbeginn 150 m³ Wasser im Becken waren. Begründen Sie, dass es sich hierbei um das maximale Wasservolumen im Beobachtungszeitraum handelt.
(6 BE)

