Schnittwinkel zweier Ebenen
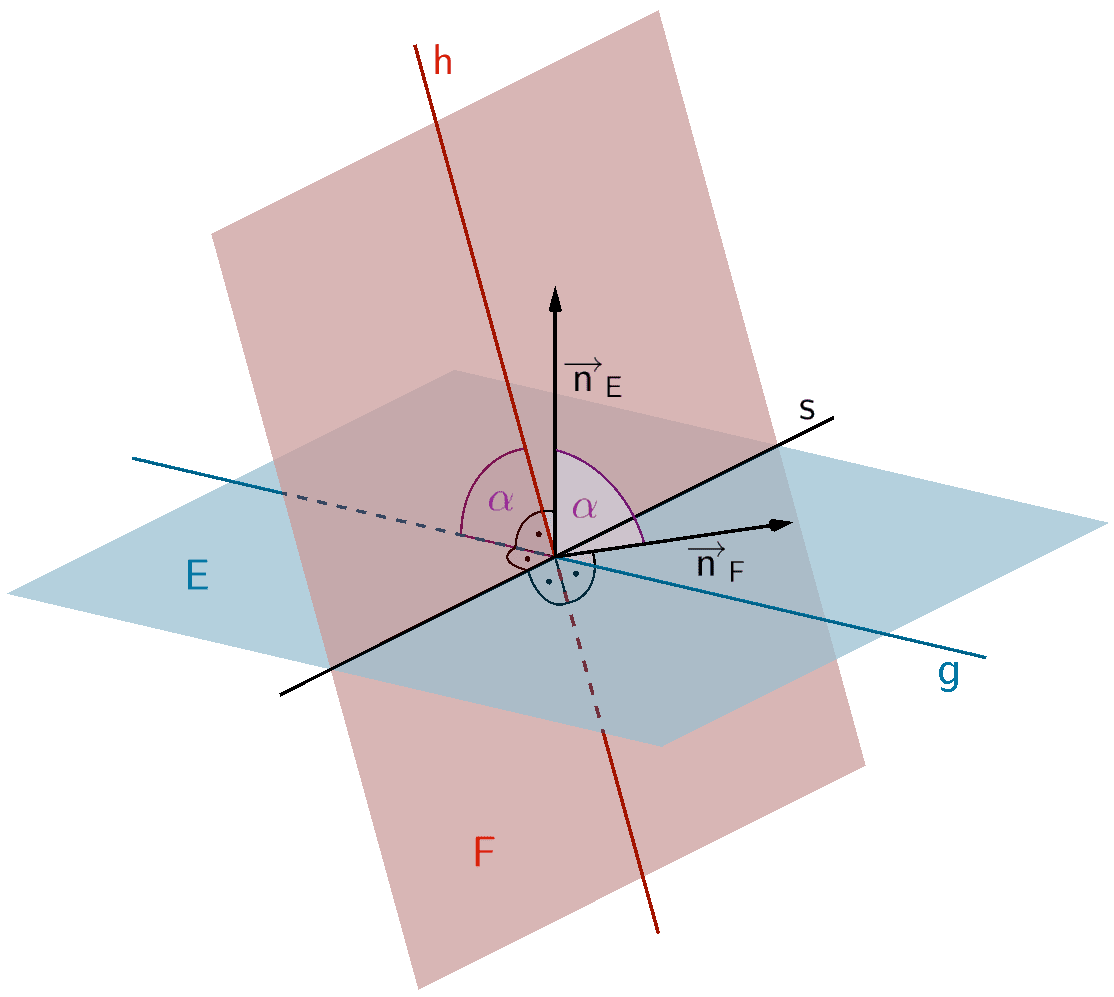
Unter dem Schnittwinkel zweier Ebenen \(E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A})\) und \(F \colon \overrightarrow{n}_{F} \circ (\overrightarrow{X} - \overrightarrow{B})\) versteht man den spitzen Winkel \(\alpha\) zwischen zwei Geraden \(g\) und \(h\), welche in demselben Punkt auf der Schnittgerade \(s\) senkrecht stehen und in der Ebene \(E\) bzw. \(F\) liegen.
Der Schnittwinkel zweier Ebenen \(E\) und \(F\) ist gleich dem spitzen Winkel \(\alpha\), den die Normalenvektoren \(\overrightarrow{n}_{E}\) und \(\overrightarrow{n}_{F}\) festlegen.
Schnittwinkel \(\boldsymbol{\alpha}\) zweier Ebenen
\[\cos \alpha = \frac{\vert \overrightarrow{n}_{E} \circ \overrightarrow{n}_{F} \vert}{\vert \overrightarrow{n}_{E} \vert \cdot \vert \overrightarrow{n}_{F} \vert} \qquad (0^{\circ} \leq \alpha \leq 90^{\circ})\]
Je nach Aufgabenstellung ist vorab der Berechnung des Schnittwinkels zweier Ebenen nachzuweisen, dass die Ebenen sich schneiden (vgl. Abiturskript - 2.3.3 Lagebeziehung von Ebenen).
Beispielaufgabe
Gegeben seien die Ebenen \(E \colon \overrightarrow{X} = \begin{pmatrix} 5 \\ 1 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ -2 \\ 2 \end{pmatrix} + \mu \cdot \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}; \; \lambda, \mu \in \mathbb R\) und \(F \colon -x_{1} +2x_{2} - 3x_{3} - 10 = 0\).
Zeigen Sie, dass sich die Ebenen \(E\) und \(F\) schneiden und berechnen Sie den Schnittwinkel der Ebenen.
Nachweis, dass sich die Ebenen \(E\) und \(F\) schneiden
\[E \colon \overrightarrow{X} = \begin{pmatrix} 5 \\ 1 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ -2 \\ 2 \end{pmatrix} + \mu \cdot \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}; \; \lambda, \mu \in \mathbb R\]
\[F \colon -x_{1} +2x_{2} - 3x_{3} - 10 = 0\]
Die Ebenen \(E\) und \(F\) schneiden sich, wenn mindestens einer der Richtungsvektoren \(\overrightarrow{u}\) und \(\overrightarrow{v}\) der Gleichung der Ebene \(E\) und der Normalenvektor \(\overrightarrow{n}_{F}\) der Ebene \(F\) nicht zueinander senkrecht sind, oder wenn die Normalenvektoren \(\overrightarrow{n}_{E}\) und \(n_{F}\) linear unabhängig sind (vgl. Abiturskript - 2.3.3 Lagebeziehung von Ebenen). Da für die Berechnung des Schnittwinkels ohnehin der Normalenvektor \(\overrightarrow{n}_{E}\) benötigt wird, ist es sinnvoll, die lineare Unabhängigkeit der Normalenvektoren \(\overrightarrow{n}_{E}\) und \(\overrightarrow{n}_{F}\) nachzuweisen.
Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) ermitteln:
\[E \colon \overrightarrow{X} = \begin{pmatrix} 5 \\ 1 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ -2 \\ 2 \end{pmatrix} + \mu \cdot \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}; \; \lambda, \mu \in \mathbb R\]
\[\Longrightarrow \quad \overrightarrow{u} = \begin{pmatrix} 3 \\ -2 \\ 2 \end{pmatrix}; \; \overrightarrow{v} = \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}\]
\[\begin{align*} \overrightarrow{u} \times \overrightarrow{v} &= \begin{pmatrix} 3 \\ -2 \\ 2 \end{pmatrix} \times \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} (-2) & \cdot & 2 & - & 2 & \cdot & 1 \\ 2 & \cdot & 2 & - & 3 & \cdot & 2 \\ 3 & \cdot & 1 & - & (-2) & \cdot & 2 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} -6 \\ -2 \\ 7 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} -6 \\ -2 \\ 7 \end{pmatrix}\]
Lineare (Un-)Abhängigkeit der Normalenvektoren \(\overrightarrow{n}_{E}\) und \(\overrightarrow{n}_{F}\) prüfen (vgl. Abiturskript - 2.1.2 Lineare (Un-)Abhängigkeit von Vektoren):
\[\overrightarrow{n}_{E} = \begin{pmatrix} -6 \\ -2 \\ 7 \end{pmatrix}\]
\[F \colon -x_{1} +2x_{2} - 3x_{3} - 10 = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{F} = \begin{pmatrix} -1 \\ 2 \\ -3 \end{pmatrix}\]
\[\Longrightarrow \quad \begin{pmatrix} -6 \\ -2 \\ 7 \end{pmatrix} \neq k \cdot \begin{pmatrix} -1 \\ 2 \\ -3 \end{pmatrix}; \; k \in \mathbb R\]
\(\Longrightarrow \quad\)Die Normalenvektoren \(\overrightarrow{n}_{E}\) und \(\overrightarrow{n}_{F}\) sind linear unabhängig.
\(\Longrightarrow \quad\)Die Ebenen \(E\) und \(F\) schneiden sich.
Schnittwinkel \(\alpha\) der Ebenen \(E\) und \(F\)
\[\overrightarrow{n}_{E} = \begin{pmatrix} -6 \\ -2 \\ 7 \end{pmatrix}; \; \overrightarrow{n}_{F} = \begin{pmatrix} -1 \\ 2 \\ -3 \end{pmatrix}\]
\[\begin{align*} \cos \alpha &= \frac{\vert \overrightarrow{n}_{E} \circ \overrightarrow{n}_{F} \vert}{\vert \overrightarrow{n}_{E} \vert \cdot \vert \overrightarrow{n}_{F} \vert} \\[0.8em] &= \frac{\left| \begin{pmatrix} -6 \\ -2 \\ 7 \end{pmatrix} \circ \begin{pmatrix} -1 \\ 2 \\ -3 \end{pmatrix} \right|}{\left| \begin{pmatrix} -6 \\ -2 \\ 7 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} -1 \\ 2 \\ -3 \end{pmatrix} \right|} \\[0.8em] &= \frac{\vert (-6) \cdot (-1) + (-2) \cdot 2 + 7 \cdot (-3) \vert}{\sqrt{(-6)^{2} + (-2)^{2} + 7^{2}} \cdot \sqrt{(-1)^{2} + 2^{2} + (-3)^{2}}} \\[0.8em] &= \frac{19}{\sqrt{89} \cdot \sqrt{14}} \qquad | \; \text{TR:} \; \cos^{-1}\left( \dfrac{19}{\sqrt{89} \cdot \sqrt{14}} \right) \\[3.2em] \alpha &\approx 57{,}43^{\circ} \end{align*}\]


