Ortskurve/Trägergraph einer Funktionenschar

Betrachtet wird die Schar der in \(\mathbb R\) definierten Funktionen \(g_k \colon x \mapsto 3x \cdot e^{kx}\) mit \(k \in \mathbb R \backslash \{0\}\). Der Graph jeder Funktion \(g_k\) der Schar hat genau einen Extrempunkt \(E_k\). Abbildung 2 zeigt den Graphen \(G\) einer Funktion dieser Schar.

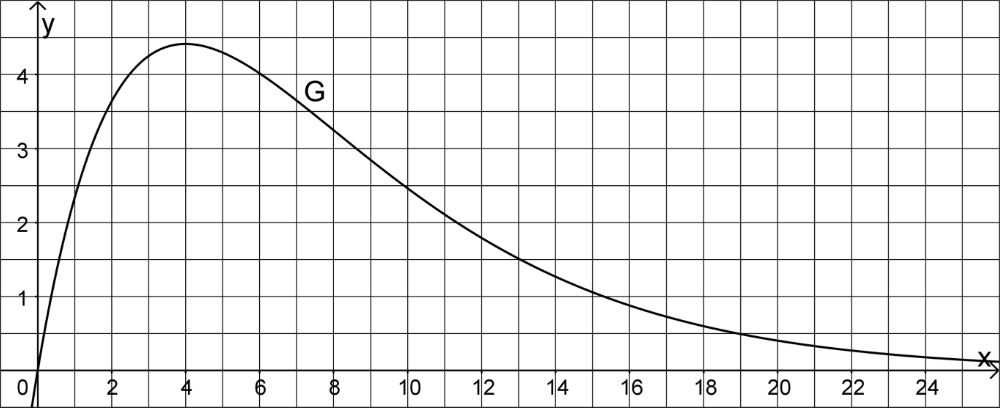Abb. 2

Alle Extrempunkte \(E_k\) liegen auf der Gerade \(h\). Bestimmen Sie rechnerisch die Steigung von \(h\).

(5 BE)

Alle Extrempunkte der Graphen der Schar liegen auf einer Gerade. Begründen Sie, dass es sich dabei um die Gerade mit der Gleichung \(y = x\) handelt.

(3 BE)