Lagebeziehung zweier Ebenen
Bei der gegenseitigen Lage zweier Ebenen \(E\) und \(F\) lassen sich drei Fälle unterscheiden:
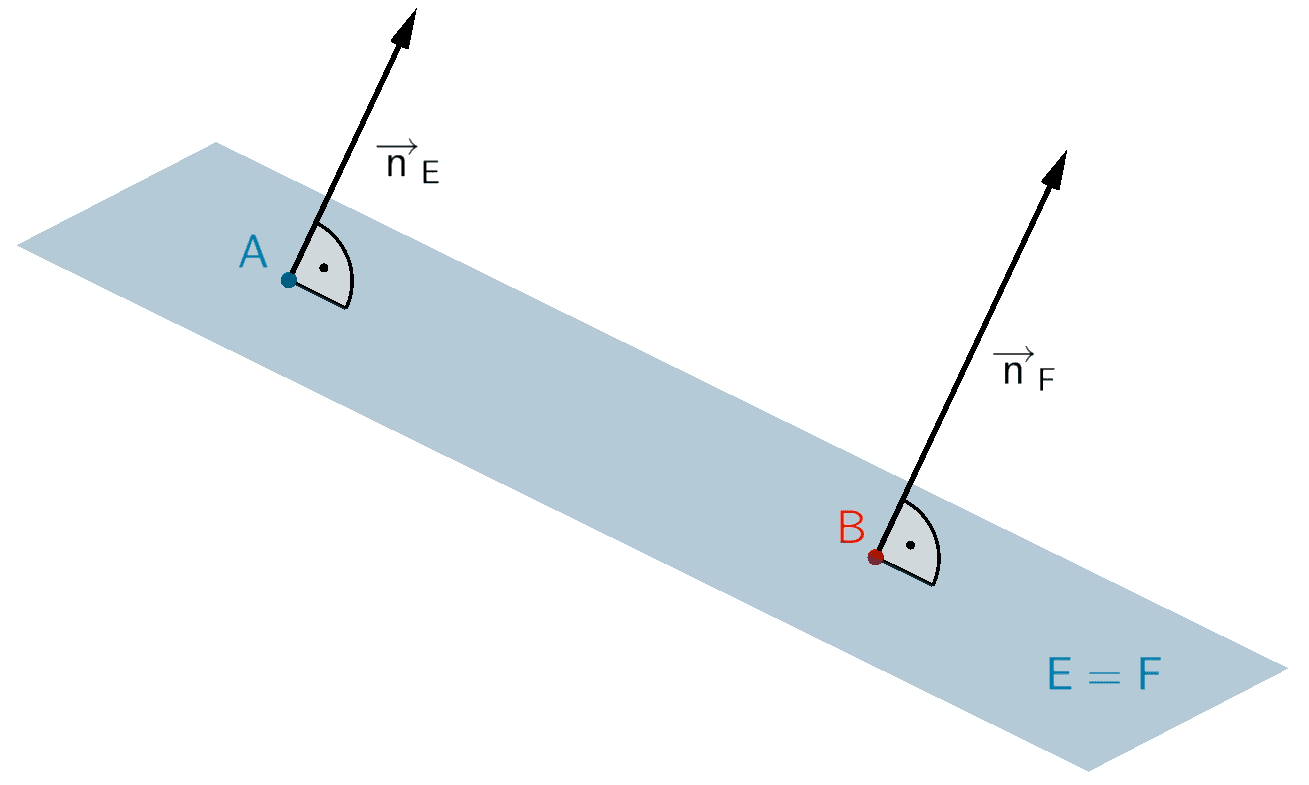
Die Ebenen \(E\) und \(F\) sind identisch.
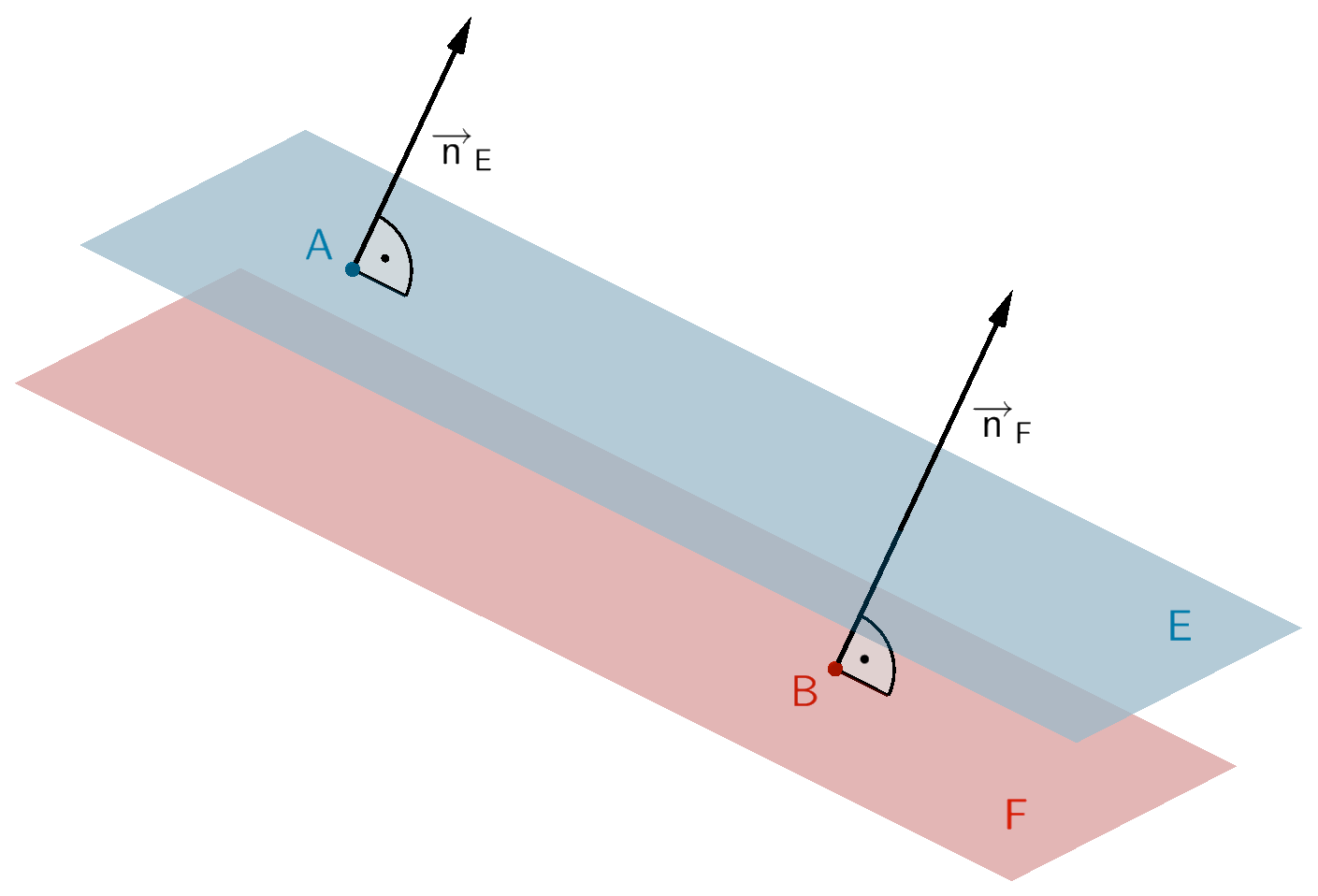
Die Ebenen \(E\) und \(F\) sind (echt) parallel.
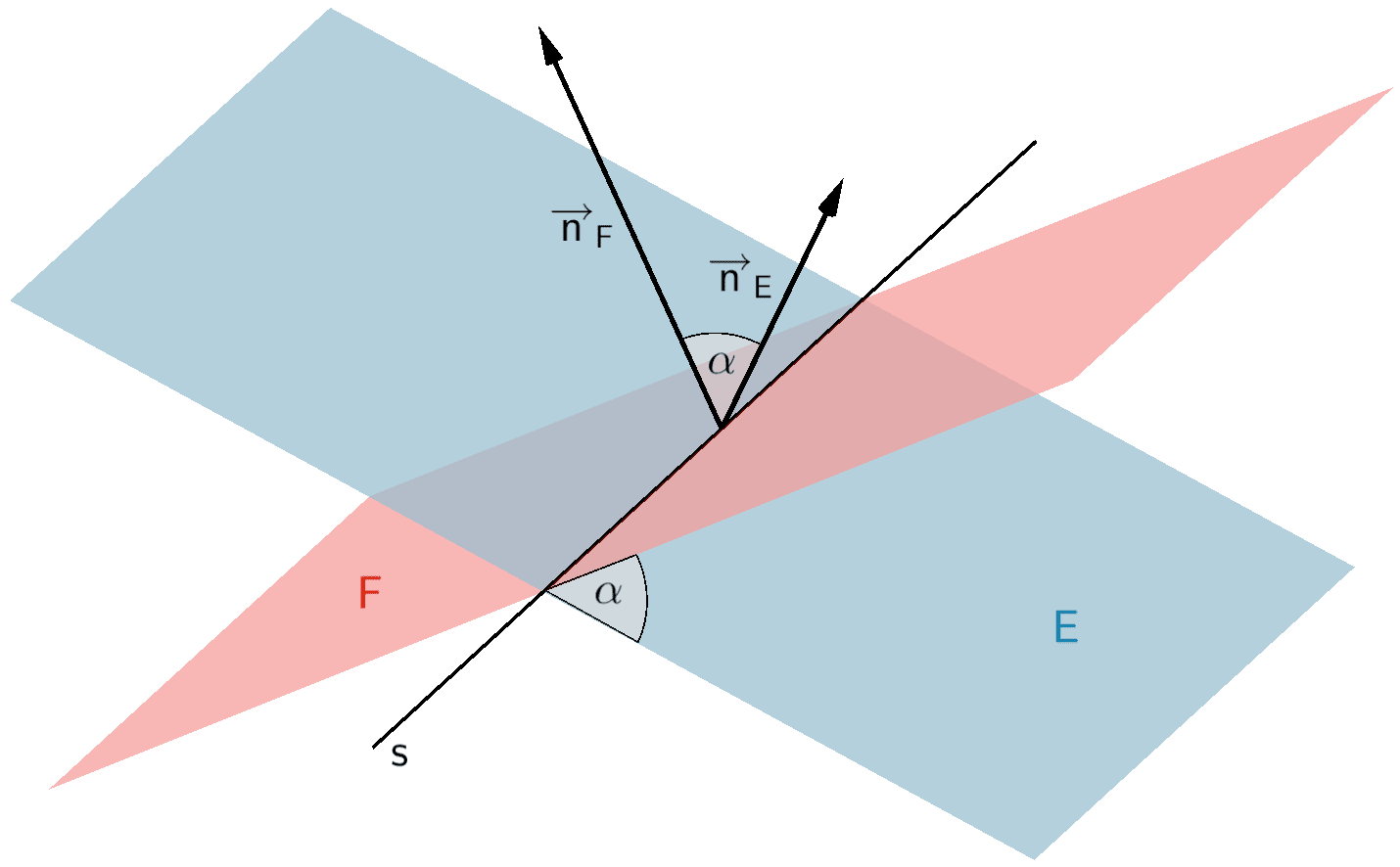
Die Ebenen \(E\) und \(F\) schneiden sich in einer Schnittgeraden \(s\) unter einem Schnittwinkel \(\alpha\).
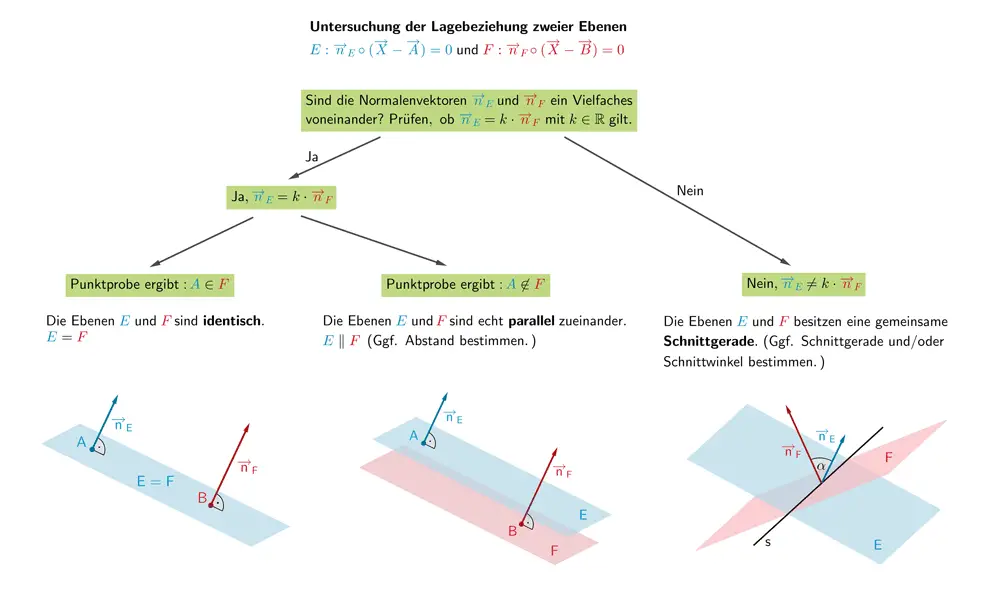
Untersuchung der Lagebeziehung zweier Ebenen
Die Vorgehensweise für die Untersuchung der gegenseitigen Lage zweier Ebenen \(E\) und \(F\) hängt von der Form der vorliegenden Ebenengleichungen ab.
Für die Untersuchung der gegenseitigen Lage zweier Ebenen \(E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\) und \(F \colon \overrightarrow{n}_{F} \circ (\overrightarrow{X} - \overrightarrow{B}) = 0\) untersucht man die Lineare (Un-)Abhängigkeit der Normalenvektoren \(\overrightarrow{n}_{E}\) und \(\overrightarrow{n}_{F}\) (vgl. Abiturskript - 2.1.2 Lineare (Un-)Abhängigkeit von Vektoren).
Für die Untersuchung der gegenseitigen Lage zweier Ebenen \(E \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} + \mu \cdot \overrightarrow{v}\,; \; \lambda, \mu \in \mathbb R\) und \(F \colon \overrightarrow{n}_{F} \circ (\overrightarrow{X} - \overrightarrow{B}) = 0\) überprüft man, ob die Richtungsvektoren \(\overrightarrow{u}\) und \(\overrightarrow{v}\) und der Normalenvektor \(\overrightarrow{n}_{F}\) zueinander senkrecht sind. (vgl. Abiturskript - 2.1.3 Skalarprodukt von Vektoren, Anwendungen des Skalarprodukts).
Liegen die Gleichung beider Ebenen \(E\) und \(F\) in der Parameterform vor, ermittelt man zunächst mithilfe des Vektorprodukts der Richtungsvektoren einer Ebenengleichung mindestens einen Normalenvektor \(\overrightarrow{n}_{E}\) bzw. \(\overrightarrow{n}_{F}\) (vgl. Abiturskript - 2.2.4 Umwandlung: Parameterform - Normalenform).
![]() Untersuchung der Lagebeziehung zweier Ebenen
Untersuchung der Lagebeziehung zweier Ebenen
Man überprüft zuerst die Lineare (Un-)Abhängigkeit der Normalenvektoren \(\overrightarrow{n}_{E}\) und \(\overrightarrow{n}_{F}\) (vgl. Abiturskript - 2.1.2 Lineare (Un-)Abhängigkeit von Vektoren) bzw. die Gültigkeit der Gleichungen \(\overrightarrow{u} \circ \overrightarrow{n}_{F} = 0\) und \(\overrightarrow{v} \circ \overrightarrow{n}_{F} = 0\) (vgl. Abiturskript - 2.1.3 Skalarprodukt von Vektoren, Anwendungen des Skalarprodukts).
Gilt \(\overrightarrow{n}_{E} = k \cdot \overrightarrow{n}_{F}\,, \; k \in \mathbb R\) bzw. \(\overrightarrow{u} \circ \overrightarrow{n}_{F} = 0\) und \(\overrightarrow{v} \circ \overrightarrow{n}_{F} = 0\), sind \(\overrightarrow{n}_{E}\) und \(\overrightarrow{n}_{F}\) linear abhängig und damit parallel zueinander bzw. \(\overrightarrow{u}\) und \(\overrightarrow{n}_{F}\) sowie \(\overrightarrow{v}\) und \(\overrightarrow{n}_{F}\) zueinander senkrecht. Die Ebenen \(E\) und \(F\) können dann identisch oder (echt) parallel sein. Erfüllt ein Aufpunkt der einen Ebenengleichung die Gleichung der anderen Ebene (Punktprobe), sind die Ebenen \(E\) und \(F\) identisch. Andernfalls sind die Ebenen (echt) parallel zueinander.
Gilt dagegen \(\overrightarrow{n}_{E} \neq k \cdot \overrightarrow{n}_{F}\,, \;k \in \mathbb R\) bzw. \(\overrightarrow{u} \circ \overrightarrow{n}_{F} \neq 0\) und/oder \(\overrightarrow{v} \circ \overrightarrow{n}_{F} \neq 0\), schneiden sich die Ebenen \(E\) und \(F\) in einer Schnittgeraden \(s\) (vgl. Bestimmung der Schnittgeraden zweier Ebenen) unter dem Schnittwinkel \(\alpha\) (vgl. Abiturskript - 2.5.3 Schnittwinkel zwischen zwei Ebenen).
Liegen die Gleichungen beider Ebenen \(E\) und \(F\) in der Normalenform in Koordinatendarstellung \(n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\) vor, lässt sich die Identität bzw. Parallelität der Ebenen durch Äquivalenzumformung der Ebenengleichungen untersuchen. Kann die Gleichung der Ebene \(F\) durch geeignete Umformung in die Gleichung der Ebene \(E\) umgewandelt werden (oder umgekehrt), sind die Ebenen \(E\) und \(F\) identisch. Unterscheiden sich die Ebenen \(E\) und \(F\) nur im Wert des konstanten Terms \(n_{0}\), sind die Ebenen \(E\) und \(F\) (echt) parallel.
Bestimmung der Schnittgerade zweier Ebenen
Die Vorgehensweise für die Bestimmung der Schnittgerade \(s\) zweier Ebenen \(E\) und \(F\) hängt von der Form der vorliegenden Ebenengleichungen ab.
Beide Ebenengleichungen in Normalenform
Für die Bestimmung der Schnittgeraden \(s\) zweier Ebenen \(E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\) und \(F \colon \overrightarrow{n}_{F} \circ (\overrightarrow{X} - \overrightarrow{B}) = 0\) ergibt sich mithilfe der Normalenform in Koordinatendarstellung ein unterbestimmtes lineares Gleichungssystem mit zwei Gleichungen und drei Unbekannten (\(x_{1}, x_{2}, x_{3}\)).
\[E \colon n_{1_{E}}x_{1} + n_{2_{E}}x_{2} + n_{3_{E}}x_{3} + n_{0_{E}} = 0\]
\[F \colon n_{1_{F}}x_{1} + n_{2_{F}}x_{2} + n_{3_{F}}x_{3} + n_{0_{F}} = 0\]
\[\Longrightarrow \enspace \left\{ \begin{align*} \text{I} & & & n_{1_{E}}x_{1} + n_{2_{E}}x_{2} + n_{3_{E}}x_{3} + n_{0_{E}} = 0 \\[0.8em] \text{II} & & \wedge \enspace &n_{1_{F}}x_{1} + n_{2_{F}}x_{2} + n_{3_{F}}x_{3} + n_{0_{F}} = 0 \end{align*} \right.\]
Dieses unterbestimmte Gleichungssystem kann nur in Abhängigkeit einer frei wählbaren Variablen gelöst werden. Man besetzt eine der Koordinaten \(x_{1}\), \(x_{2}\) oder \(x_{3}\) mit einem Parameter, beispielsweise \(x_{1} = \lambda\) mit \(\lambda \in \mathbb R\), und löst das Gleichungssystem in Abhängigkeit dieses Parameters. Damit lassen sich alle drei Koordinaten \(x_{1}\), \(x_{2}\) und \(x_{3}\) des Ortsvektors eines beliebigen Punktes \(X\) der Schnittgeraden \(s\) in Abhängigkeit des Parameters \(\lambda\) formulieren. Durch Umformen erhält man die Parameterform der Geradengleichung der Schnittgeraden.
Beispiel:
Bestimmen Sie die Schnittgerade \(s\) der Ebenen \(E \colon x_{1} + x_{2} + 3x_{3} - 3 = 0\) und \(F \colon -x_{1} - x_{2} + 3x_{3} - 3 = 0\).
\[E \colon x_{1} + x_{2} + 3x_{3} - 3 = 0\]
\[F \colon -x_{1} - x_{2} + 3x_{3} - 3 = 0\]
Die Schnittgerade \(s\) beschreibt die Menge aller Punkte \(X\), welche sowohl in der Ebene \(E\) als auch in der Ebene \(F\) liegen. Folglich gelten beide Ebenengleichungen zugleich, d.h. sie bilden ein Gleichungssystem.
\[\Longrightarrow \enspace \left\{ \begin{align*} \text{I} & & & \quad \; x_{1} + x_{2} + 3x_{3} - 3 = 0 \\[0.8em] \text{II} & & \wedge \enspace &-x_{1} - x_{2} + 3x_{3} - 3 = 0 \end{align*} \right.\]
Eine Koordinate mit einem Parameter besetzen, z.B. \(x_{1} = \lambda\) mit \(\lambda \in \mathbb R\):
\[\Longrightarrow \enspace \left\{ \begin{align*} \text{I} & & & \quad \; \lambda + x_{2} + 3x_{3} - 3 = 0 \\[0.8em] \text{II} & & \wedge \enspace &-\lambda - x_{2} + 3x_{3} - 3 = 0 \end{align*} \right.\]
Gleichungssystem in Abhängigkeit des Parameters \(\lambda\) lösen:
Das vorliegende lineare Gleichungssystem lässt sich z.B. mit dem Additionsverfahren (hier Subtraktion) lösen. Der Rechenschritt \(\text{I} - \text{II}\) „eliminiert" den Summanden \(3x_{3}\) und man erhält eine Gleichung zur Bestimmung von \(x_{2}\) in Abhängigkeit von \(\lambda\).
\[\begin{align*} \text{I} - \text{II} \colon \; \lambda - (-\lambda) + x_{2} - (-x_{2}) + 3x_{3} - 3x_{3} - 3 - (-3) &= 0 \\[0.8em] 2\lambda + 2x_{2} &= 0 & &| - 2\lambda \\[0.8em] 2x_{2} &= -2\lambda & &| : 2 \\[0.8em] x_{2} &= -\lambda \end{align*}\]
\[\begin{align*} x_{1} = \lambda, x_{2} = -\lambda \; \text{in I} \colon \; \lambda - \lambda +3x_{3} - 3 &= 0 \\[0.8em] 3x_{3} - 3 &= 0 & &| + 3 \\[0.8em] 3x_{3} &= 3 & &| : 3 \\[0.8em] x_{3} &= 1 \end{align*}\]
Mit \(x_{1} = \lambda\), \(x_{2} = -\lambda\) und \(x_{3} = 1\) lässt sich der Ortsvektor eines beliebigen Punktes \(X\) der Schnittgeraden \(s\) in Abhängigkeit des Parameters \(\lambda\) formulieren.
\[\overrightarrow{X} = \begin{pmatrix} \lambda \\ -\lambda \\ 1 \end{pmatrix}; \; \lambda \in \mathbb R\]
Abschließend formuliert man den Ortsvektor \(\overrightarrow{X}\) in der nach dem Ortsvektor des Aufpunkts und dem Richtungsvektor getrennten Schreibweise \(\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\) und erhält dadurch die Parameterform der Geradengleichung der Schnittgerade \(s\).
\[\overrightarrow{X} = \begin{pmatrix} \lambda \\ -\lambda \\ 1 \end{pmatrix} = \begin{pmatrix} 0 + \lambda \\ 0 - \lambda \\ 1 + 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}\]
\[\Longrightarrow \quad s \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}; \; \lambda \in \mathbb R\]
Je eine Ebenengleichung in Normalenform bzw. Parameterform
Für die Bestimmung der Schnittgerade \(s\) zweier Ebenen \(E \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} + \mu \cdot \overrightarrow{v}\,; \; \lambda, \mu \in \mathbb R\) und \(F \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\) setzt man die Koordinaten des Ortsvektors \(\overrightarrow{X}\) der Gleichung der Ebene \(E\) in Parameterform in die Gleichung der Ebene \(F\) in Normalenform in Koordinatendarstellung ein. Anschließend löst man die Gleichung nach dem Parameter \(\lambda\) in Abhängigkeit des Parameters \(\mu\) auf oder umgekehrt. Das Ergebnis setzt man in die Gleichung der Ebene \(E\) in Parameterform ein und erhält dadurch den Ortsvektor eines beliebigen Punktes \(X\) der Schnittgeraden \(s\) in Abhängigkeit von \(\lambda\) bzw. \(\mu\). Die Parametrform der Geradengleichung der Schnittgerade \(s\) ergibt sich durch die Formulierung des Ortsvektors \(\overrightarrow{X}\) in der nach dem Ortsvektor des Aufpunkts und dem Richtungsvektor getrennten Schreibweise \(\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\) bzw. \(\overrightarrow{X} = \overrightarrow{A} + \mu \cdot \overrightarrow{v}\).
Beispiel:
Bestimmen Sie die Schnittgerade \(s\) der Ebenen \(E \colon \overrightarrow{X} = \begin{pmatrix} -6{,}5 \\ 0 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 2 \\ 0 \end{pmatrix} + \mu \cdot \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}; \; \lambda, \mu \in \mathbb R\) und \(F \colon -5x_{1} + 4x_{2} - 2x_{3} - 8 = 0\)
\[E \colon \overrightarrow{X} = \begin{pmatrix} -6{,}5 \\ 0 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 2 \\ 0 \end{pmatrix} + \mu \cdot \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}; \; \lambda, \mu \in \mathbb R\]
\[F \colon -5x_{1} + 4x_{2} - 2x_{3} - 8 = 0\]
Koordinaten des Ortsvektors \(\overrightarrow{X}\) der Gleichung der Ebene \(E\) in die Gleichung der Ebene \(F\) einsetzen und die Gleichung nach dem Parameter \(\lambda\) in Abhängigkeit von \(\mu\) (oder umgekehrt) auflösen.
\[E \colon \overrightarrow{X} = \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \end{pmatrix} = \begin{pmatrix} -6{,}5 + 3\lambda + \mu \\ 2\lambda \\ \mu \end{pmatrix}\]
\[\begin{align*} E \cap F \colon -5 \cdot (-6{,}5 + 3\lambda + \mu) + 4 \cdot 2\lambda - 2 \cdot \mu - 8 &= 0 \\[0.8em] -32{,}5 - 15\lambda - 5\mu + 8\lambda - 2\mu - 8 &= 0 \\[0.8em] 24{,}5 - 7\lambda -7\mu &= 0 & &| + 7\mu \\[0.8em] 24{,}5 - 7\lambda &= 7\mu & &| : 7 \\[0.8em] 3{,}5 - \lambda &= \mu \end{align*}\]
Das Ergebnis \(\mu = 3{,}5 - \lambda\) in die Gleichung der Ebene \(E\) einsetzen und den Ortsvektor \(\overrightarrow{X}\) in der nach dem Ortsvektor des Aufpunkts und dem Richtungsvektor getrennten Schreibweise \(\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\) formulieren.
\[E \colon \overrightarrow{X} = \begin{pmatrix} -6{,}5 \\ 0 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 2 \\ 0 \end{pmatrix} + \mu \cdot \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}\]
\[\begin{align*}\overrightarrow{X} &= \begin{pmatrix} -6{,}5 \\ 0 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 2 \\ 0 \end{pmatrix} + (3{,}5 - \lambda) \cdot \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} -6{,}5 \\ 0 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 2 \\ 0 \end{pmatrix} + \begin{pmatrix} 3{,}5 \\ 0 \\ 3{,}5 \end{pmatrix} - \lambda \cdot \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} -3 \\ 0 \\ 3{,}5 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 2 \\ 2 \\ -1 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad s \colon \overrightarrow{X} = \begin{pmatrix} -3 \\ 0 \\ 3{,}5 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 2 \\ 2 \\ -1 \end{pmatrix}; \; \lambda \in \mathbb R\]
Beide Ebenengleichungen in Parameterform
Liegen beide Gleichungen der Ebenen \(E\) und \(F\) in der Parameterform vor, ist es für die Bestimmung der Schnittgerade \(s\) zweckmäßig, eine der Ebenengleichungen in die Normalenform in Koordinatendarstellung umzuwandeln (vgl. Abiturskript - 2.2.4 Umwandlung: Parameterform - Normalenform). Andernfalls muss unter größerem Rechenaufwand ein unbestimmtes Gleichungssystem mit drei Gleichungen und vier Unbekannten (je zwei Parameter der Ebenengleichungen) in Abhängigkeit eines Parameters gelöst werden, um die Geradenleichung der Schnittgerade \(s\) formulieren zu können.
Beispielaufgabe
Geben seien die Ebenen \(E\), \(F\), \(G\) und \(H\) mit den Gleichungen:
\[E \colon 3x_{1} - 2x_{2} + x_{3} - 3 = 0\]
\[F \colon -6x_{1} + 4x_{2} -2x_{3} + 6 = 0\]
\[G \colon -3x_{1} + 2x_{2} - x_{3} + 12 = 0\]
\[H \colon \overrightarrow{X} = \begin{pmatrix} -4 \\ 4 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix} + \mu \cdot \begin{pmatrix} 0 \\ 1 \\ -3 \end{pmatrix}; \; \lambda, \mu \in \mathbb R\]
Untersuchen Sie die gegenseitige Lage der Ebenen \(E\) und \(F\), der Ebenen \(E\) und \(G\) sowie der Ebenen \(E\) und \(H\) und ermitteln Sie gegebenenfalls eine Gleichung der Schnittgerade \(s\).
Lagebeziehung der Ebenen \(E\) und \(F\)
\[E \colon 3x_{1} - 2x_{2} + x_{3} - 3 = 0\]
\[F \colon -6x_{1} + 4x_{2} -2x_{3} + 6 = 0\]
1. Möglichkeit: Äquivalenzumformung einer der Ebenengleichungen
Die Gleichungen beider Ebenen \(E\) und \(F\) liegen in der Normalenform in Koordinatendarstellung vor. Es bietet sich an, die Ebenen durch Äquivalenzumformung einer der Ebenengleichungen auf Identität bzw. Parallelität hin zu untersuchen.
\[E \colon 3x_{1} - 2x_{2} + x_{3} - 3 = 0\]
\[\begin{align*}F \colon -6x_{1} + 4x_{2} -2x_{3} + 6 &= 0 & &| : (-2) \\[0.8em] 3x_{1} - 2x_{2} + x_{3} - 3 &= 0 \end{align*}\]
\[\Longrightarrow \quad E = F \colon 3x_{1} - 2x_{2} + x_{3} - 3 = 0\]
\(\Longrightarrow \quad\)Die Ebenen \(E\) und \(F\) sind identisch.
2. Möglichkeit: Lineare (Un-)Abhängigkeit der Normalenvektoren und ggf. Punktprobe
Die beiden Ebenen \(E\) und \(F\) liegen in der Normalenform (in Koordinatendarstellung) vor. Für die Untersuchung der gegenseitigen Lage der Ebenen wird zuerst die Lineare (Un-)Abhängigkeit der Normalenvektoren \(\overrightarrow{n}_{E}\) und \(\overrightarrow{n}_{F}\) überprüft (vgl. Abiturskript - 2.1.2 Lineare (Un-)Abhängigkeit von Vektoren).
\[E \colon 3x_{1} - 2x_{2} + x_{3} - 3 = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 3 \\ -2 \\ 1 \end{pmatrix}\]
\[F \colon -6x_{1} + 4x_{2} -2x_{3} + 6 = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{F} = \begin{pmatrix} -6 \\ 4 \\ -2 \end{pmatrix}\]
\[\begin{align*}\overrightarrow{n}_{E} &= k \cdot \overrightarrow{n}_{F}\,; \; k \in \mathbb R \\[0.8em] \begin{pmatrix} 3 \\ -2 \\ 1 \end{pmatrix} &= k \cdot \begin{pmatrix} -6 \\ 4 \\ -2 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad k = -0{,}5 \quad \Longrightarrow \quad \overrightarrow{n}_{E} \parallel \overrightarrow{n}_{F}\]
Die Normalenvektoren \(\overrightarrow{n}_{E}\) und \(\overrightarrow{n}_{F}\) sind linear abhängig. Damit können die Ebenen \(E\) und \(F\) identisch oder (echt) parallel sein.
Prüfen, ob \(E\) und \(F\) identisch sind (Punktprobe):
Da beide Gleichungen der Ebenen \(E\) und \(F\) in der Normalenform in Koordinatendarstellung vorliegen, lässt sich kein Aufpunkt für die Punktprobe ablesen. Es kann aber schnell ein Spurpunkt einer der Ebenen gefunden werden, beispielsweise der Spurpunkt \(S_{x_{3}}\) der Ebene \(E\), d.h. der Schnittpunkt der Ebene \(E\) mit der \(x_{3}\)-Achse (vgl. Abiturskript - 2.2.3 Ebenengleichung in Normalenform, Spurgerade).
\[E \colon 3x_{1} - 2x_{2} + x_{3} - 3 = 0\]
\[S_{x_{3}}(0|0|s_{3})\]
\[\begin{align*}S_{x_{3}} \in E \colon x_{3} - 3 &= 0 & &| + 3 \\[0.8em] x_{3} &= 3 \end{align*}\]
\[\Longrightarrow{S_{x_{3}}}(0|0|3)\]
\(S_{x_{3}}(0|0|3)\) in die Gleichung der Ebene \(F\) einsetzen:
\[F \colon -6x_{1} + 4x_{2} -2x_{3} + 6 = 0\]
\[\begin{align*}-6 \cdot 0 + 4 \cdot 0 - 2 \cdot 3 + 6 &= 0 \\[0.8em] 0 &= 0 \quad (\text{w}) \end{align*}\]
\[\Longrightarrow \quad S_{x_{3}} \in F\]
\(\Longrightarrow \quad\) Die Ebenen \(E\) und \(F\) sind identisch.
Lagebeziehung der Ebenen \(E\) und \(G\)
\[E \colon 3x_{1} - 2x_{2} + x_{3} - 3 = 0\]
\[G \colon -3x_{1} + 2x_{2} - x_{3} + 12 = 0\]
1. Möglichkeit: Äquivalenzumformung einer der Ebenengleichungen
Die Gleichungen beider Ebenen \(E\) und \(G\) liegen in der Normalenform in Koordinatendarstellung vor. Es bietet sich an, die Ebenen durch Äquivalenzumformung einer der Ebenengleichungen auf Identität bzw. Parallelität hin zu untersuchen.
\[E \colon 3x_{1} - 2x_{2} + x_{3} - 3 = 0\]
\[\begin{align*}&G \colon -3x_{1} + 2x_{2} - x_{3} + 12 = 0 & &| \cdot (-1) \\[0.8em] &G \colon 3x_{1} - 2x_{2} + x_{3} - 12 = 0 \end{align*}\]
Die Gleichung der Ebene \(G\) unterscheidet sich von der Gleichung der Ebene \(E\) nur im Wert des konstanten Terms \(n_{0}\).
\(\Longrightarrow \quad\)Die Ebenen \(E\) und \(G\) sind (echt) parallel.
2.Möglichkeit: Lineare (Un-)Abhängigkeit der Normalenvektoren und ggf. Punktprobe
Die beiden Ebenen \(E\) und \(G\) liegen in der Normalenform (in Koordinatendarstellung) vor. Für die Untersuchung der gegenseitigen Lage der Ebenen wird zuerst die Lineare (Un-)Abhängigkeit der Normalenvektoren \(\overrightarrow{n}_{E}\) und \(\overrightarrow{n}_{G}\) überprüft (vgl. Abiturskript - 2.1.2 Lineare (Un-)Abhängigkeit von Vektoren)
\[E \colon 3x_{1} - 2x_{2} + x_{3} - 3 = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 3 \\ -2 \\ 1 \end{pmatrix}\]
\[G \colon -3x_{1} + 2x_{2} - x_{3} + 12 = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{G} = \begin{pmatrix} -3 \\ 2 \\ -1 \end{pmatrix}\]
\[\begin{align*}\overrightarrow{n}_{E} &= k \cdot \overrightarrow{n}_{G}\,; \; k \in \mathbb R \\[0.8em] \begin{pmatrix} 3 \\ -2 \\ 1 \end{pmatrix} &= k \cdot \begin{pmatrix} -3 \\ 2 \\ -1 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad k = -1 \quad \Longrightarrow \quad \overrightarrow{n}_{E} \parallel \overrightarrow{n}_{G}\]
Die Normalenvektoren \(\overrightarrow{n}_{E}\) und \(\overrightarrow{n}_{G}\) sind linear abhängig (kollinear). Damit können die Ebenen \(E\) und \(G\) identisch oder (echt) parallel sein.
Prüfen, ob \(E\) und \(G\) identisch sind (Punktprobe):
Da beide Gleichungen der Ebenen \(E\) und \(G\) in der Normalenform in Koordinatendarstellung vorliegen, lässt sich kein Aufpunkt für die Punktprobe ablesen. Es kann aber schnell ein Spurpunkt einer der Ebenen gefunden werden, beispielsweise der Spurpunkt \(S_{x_{3}}\) der Ebene \(E\), d.h. der Schnittpunkt der Ebene \(E\) mit der \(x_{3}\)-Achse (vgl. Abiturskript - 2.2.3 Ebenengleichung in Normalenform, Spurgerade).
\[E \colon 3x_{1} - 2x_{2} + x_{3} - 3 = 0\]
\[S_{x_{3}}(0|0|s_{3})\]
\[\begin{align*}S_{x_{3}} \in E \colon x_{3} - 3 &= 0 & &| + 3 \\[0.8em] x_{3} &= 3 \end{align*}\]
\[\Longrightarrow{S_{x_{3}}}(0|0|3)\]
\(S_{x_{3}}(0|0|3)\) in die Gleichung der Ebene \(G\) einsetzen:
\[G \colon -3x_{1} + 2x_{2} - x_{3} + 12 = 0\]
\[\begin{align*}-3 \cdot 0 + 2 \cdot 0 - 3 + 12 &= 0 \\[0.8em] 9 &= 0 \quad (\text{f}) \end{align*}\]
\[\Longrightarrow \quad S_{x_{3}} \notin G\]
\(\Longrightarrow \quad\) Die Ebenen \(E\) und \(G\) sind (echt) parallel.
Lagebeziehung der Ebenen \(E\) und \(H\)
\[E \colon 3x_{1} - 2x_{2} + x_{3} - 3 = 0\]
\[H \colon \overrightarrow{X} = \begin{pmatrix} -4 \\ 4 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix} + \mu \cdot \begin{pmatrix} 0 \\ 1 \\ -3 \end{pmatrix}; \; \lambda, \mu \in \mathbb R\]
Die Gleichung der Ebenen \(E\) liegt in der Normalenform vor und die Gleichung der Ebene \(H\) liegt in der Parameterform vor. Mithilfe des Skalarprodukts wird zunächst untersucht, ob der Normalenvektor der Gleichung der Ebenen \(E\) senkrecht zu einem Richtungsvektor der Gleichung der Ebenen \(H\) ist (vgl.Abiturskript - 2.1.3 Skalarprodukt von Vektoren, Anwendungen des Skalarprodukts).
\[E \colon 3x_{1} - 2x_{2} + x_{3} - 3 = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 3 \\ -2 \\ 1 \end{pmatrix}\]
\[H \colon \overrightarrow{X} = \begin{pmatrix} -4 \\ 4 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix} + \mu \cdot \begin{pmatrix} 0 \\ 1 \\ -3 \end{pmatrix}\]
\(\overrightarrow{u} = \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix}\) und \(\overrightarrow{v} = \begin{pmatrix} 0 \\ 1 \\ -3 \end{pmatrix}\) sind Richtungsvektor der Gleichung der Ebenen \(H\).
Prüfen, ob beide Richtungsvektoren \(\overrightarrow{u}\) und \(\overrightarrow{v}\) der Gleichung der Ebene \(H\) senkrecht zum Normalenvektor \(\overrightarrow{n}_{E}\) der Gleichung der Ebene \(E\) sind:
\[\begin{align*} \overrightarrow{n}_{E} \circ \overrightarrow{u} &= 0 \\[0.8em] \begin{pmatrix} 3 \\ -2 \\ 1 \end{pmatrix} \circ \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix} &= 0 \\[0.8em] 3 \cdot 1 + (-2) \cdot 0 + 1 \cdot (-3) &= 0 \\[0.8em] 3 - 3 &= 0 \quad (\text{w}) \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{u} \perp \overrightarrow{n}_{E}\]
\[\begin{align*} \overrightarrow{n}_{E} \circ \overrightarrow{v} &= 0 \\[0.8em] \begin{pmatrix} 3 \\ -2 \\ 1 \end{pmatrix} \circ \begin{pmatrix} 0 \\ 1 \\ -3 \end{pmatrix} &= 0 \\[0.8em] 3 \cdot 0 + (-2) \cdot 1 + 1 \cdot (-3) &= 0 \\[0.8em] -5 &= 0 \quad (\text{f}) \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{v} \not \perp \overrightarrow{n}_{E}\]
\[\Longrightarrow \quad E \nparallel H\]
Da nicht beide Richtungsvektoren \(\overrightarrow{u}\) und \(\overrightarrow{v}\) der Ebenengleichung von \(H\) senkrecht zum Normalenvektor \(\overrightarrow{n}_{E}\) der Ebenengleichung von \(E\) sind, können die Ebenen \(E\) und \(H\) nicht parallel zueinander sein. Folglich schneiden sich die Ebenen \(E\) und \(H\) in einer Schnittgeraden \(s\).
Bestimmung einer Gleichung der Schnittgerade \(s\) der Ebenen \(E\) und \(H\)
\[E \colon 3x_{1} - 2x_{2} + x_{3} - 3 = 0\]
\[H \colon \overrightarrow{X} = \begin{pmatrix} -4 \\ 4 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix} + \mu \cdot \begin{pmatrix} 0 \\ 1 \\ -3 \end{pmatrix}; \; \lambda, \mu \in \mathbb R\]
Koordinaten des Ortsvektors \(\overrightarrow{X}\) der Gleichung der Ebene \(H\) in die Gleichung der Ebene \(E\) einsetzen und die Gleichung nach dem Parameter \(\lambda\) in Abhängigkeit von \(\mu\) (oder umgekehrt) auflösen.
\[H \colon \overrightarrow{X} = \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \end{pmatrix} = \begin{pmatrix} -4 + \lambda \\ 4 + \mu \\ 3 - 3\lambda - 3\mu \end{pmatrix}\]
\[\begin{align*} H \cap E \colon 3 \cdot (-4 + \lambda) - 2 \cdot (4 + \mu) + 3 - 3\lambda - 3\mu - 3 &= 0 \\[0.8em] -12 + 3\lambda - 8 - 2\mu + 3 - 3\lambda - 3\mu - 3 &= 0 \\[0.8em] -20 - 5\mu &= 0 & &| + 20 \\[0.8em] -5\mu &= 20 & &| : (-5) \\[0.8em] \mu &= -4 \end{align*}\]
Das Ergebnis \(\mu = -4\) (in diesem Fall nicht von \(\lambda\) abhängig) in die Gleichung der Ebene \(H\) einsetzen und den Ortsvektor \(\overrightarrow{X}\) in der nach dem Ortsvektor des Aufpunkts und dem Richtungsvektor getrennten Schreibweise \(\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\) formulieren.
\[H \colon \overrightarrow{X} = \begin{pmatrix} -4 \\ 4 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix} + \mu \cdot \begin{pmatrix} 0 \\ 1 \\ -3 \end{pmatrix}\]
\[\begin{align*}\overrightarrow{X} &= \begin{pmatrix} -4 \\ 4 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix} - 4 \cdot \begin{pmatrix} 0 \\ 1 \\ -3 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} -4 \\ 0 \\ 15 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad s \colon \overrightarrow{X} = \begin{pmatrix} -4 \\ 0 \\ 15 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix}; \; \lambda \in \mathbb R\]