Bei der Berechnung des Abstands eines Punktes von einer Ebene spielt die Hessesche Normalenform einer Ebene eine große Rolle (vgl. Abiturskript - 2.2.3 Ebenengleichung in Normalenform, Hessesche Normalenform). Setzt man die Koordinaten eines beliebigen Punktes in die Gleichung einer Ebene in der Hesseschen Normalenform ein, erhält man als Ergebnis den Abstand des Punktes von der Ebene.
Abstand eines Punktes von einer Ebene
Für den Abstand \(d(P;E)\) eines Punktes \(P(p_{1}|p_{2}|p_{3})\) zu einer in der Hesseschen Normalenform (HNF) vorliegenden Ebene \(E\) gilt:
Vektordarstellung
\[E \colon \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{P} - \overrightarrow{A}) \right|\]
Koordinatendarstellung
\[E \colon \frac{n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \frac{n_{1}p_{1} + n_{2}p_{2} + n_{3}p_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} \right|\]
Dabei ist \(\overrightarrow{n}^{0}_{E} = \dfrac{\overrightarrow{n}_{E}}{\vert \overrightarrow{n}_{E} \vert}\) der Einheitsvektor des Normalenvektors \(\overrightarrow{n}_{E}\) der Ebene \(E\).
Bei der Bestimmung des Abstands \(d(P;E)\) eines Punktes \(P\) von einer Ebene \(E\) lassen sich folgende mögliche Ergebnisse unterscheiden:
- \(d(P;E) > 0\): Der Punkt \(P\) und der Koordinatenursprung \(O\) liegen auf verschiedenen Seiten der Ebene \(E\).
- \(d(P;E) = 0\): Der Punkt \(P\) liegt in der Ebene \(E\) \((P \in E)\).
- \(d(P;E) < 0\): Der Punkt \(P\) und der Koordinatenursprung \(O\) liegen auf der gleichen Seite der Ebene \(E\).
Veranschaulichung der Abstandsbestimmung eines Punktes \(P\) von einer Ebene \(E\):
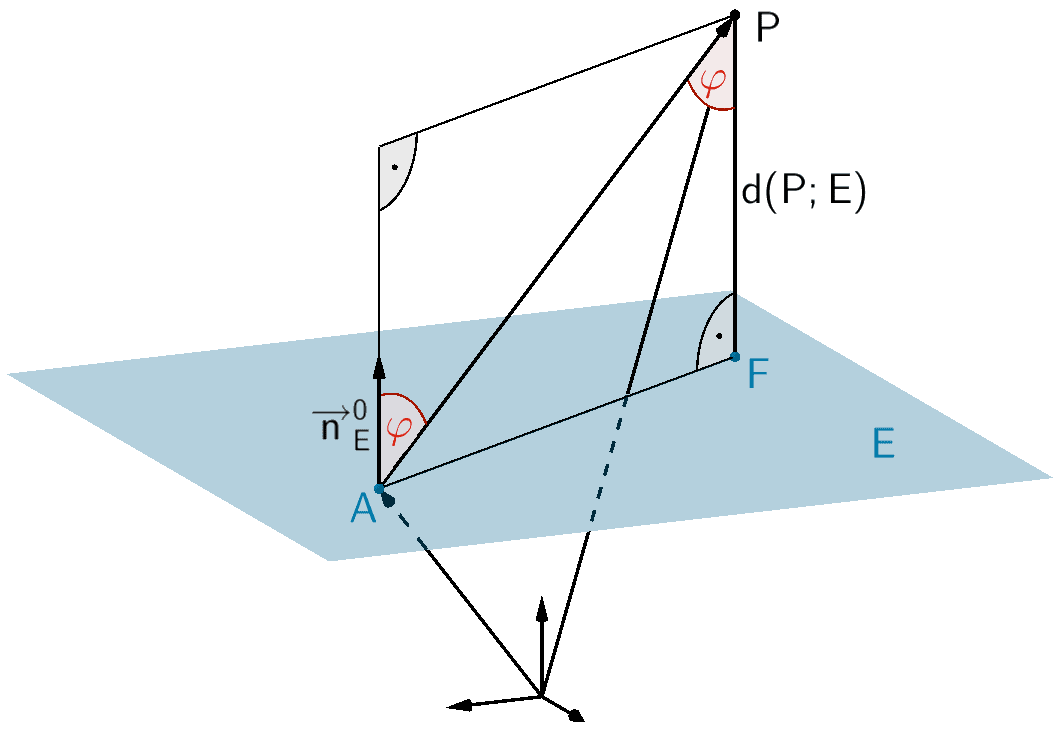
Es sei \(F\) der Lotfußpunkt des Lotes des Punktes \(P\) auf die Ebene \(E\).
Im rechtwinkligen Dreieck \(AFP\) gilt:
\[d(P;E) = \left| \vert \overrightarrow{AP} \vert \cdot \cos \varphi \right|\]
Für den Winkel \(\varphi\) zwischen dem Verbindungsvektor \(\overrightarrow{AP}\) und dem Einheitsnormalenvektor \(\overrightarrow{n}^{0}_{E}\) der Ebene \(E\) gilt (vgl. Abiturskript - 2.1.3 Skalarprodukt, Anwendungen des Skalarprodukts):
\[\cos \varphi = \frac{\overrightarrow{n}_{E}^{0} \circ \overrightarrow{AP}}{\vert \overrightarrow{n}_{E}^{0} \vert \cdot \vert \overrightarrow{AP} \vert}\]
Damit ergibt sich:
\[\begin{align*} d(P;E) &= \left| \vert \overrightarrow{AP} \vert \cdot \cos \varphi \right| \\[0.8em] &= \left| \cancel{\vert \overrightarrow{AP} \vert} \cdot \frac{\overrightarrow{n}_{E}^{0} \circ \overrightarrow{AP}}{\vert \overrightarrow{n}_{E}^{0} \vert \cdot \cancel{ \vert \overrightarrow{AP} \vert}} \right| & &| \; \vert \overrightarrow{n}_{E}^{0} \vert = 1 \\[0.8em] &= \left| \overrightarrow{n}_{E}^{0} \circ \overrightarrow{AP} \right| \\[0.8em] &= \left| \overrightarrow{n}_{E}^{0} \circ (\overrightarrow{P} - \overrightarrow{A}) \right| \end{align*}\]
Lotfußpunktverfahren
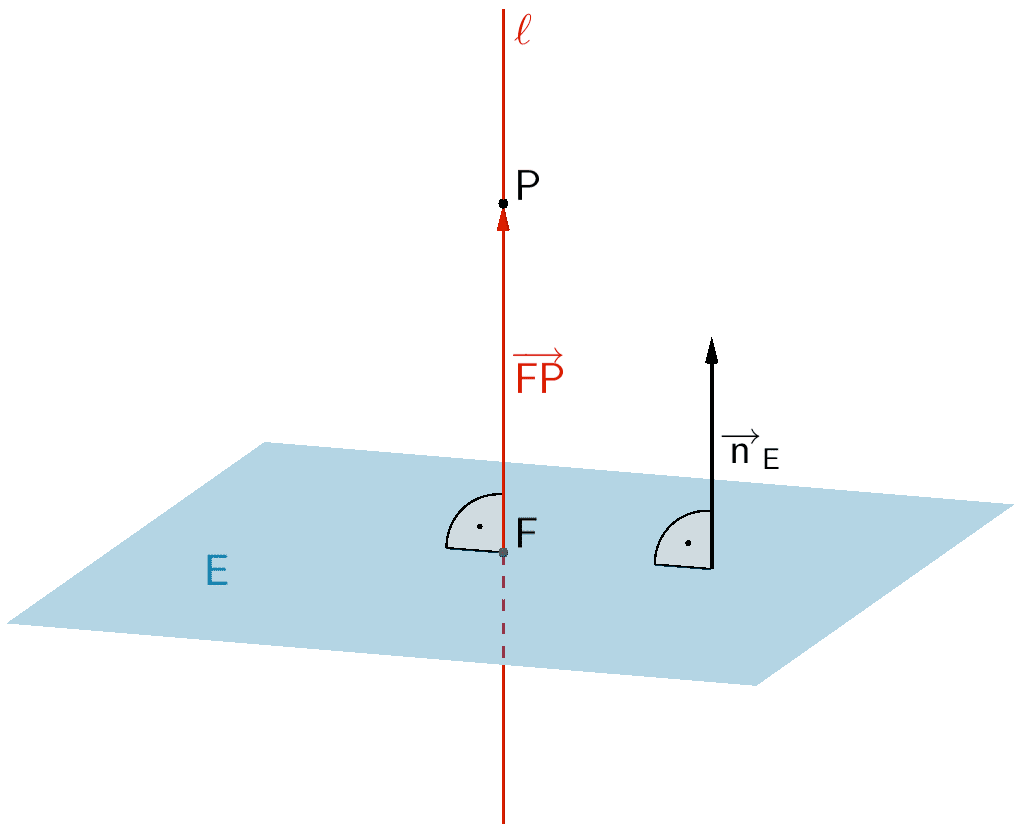
Beim Lotfußpunktverfahren wird zunächst die Lotgerade \(\ell\) durch den Punkt \(P\) zur Ebene \(E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A})\) aufgestellt (vgl. Abiturskript - 2.3.4 Lotgeraden und orthogonale Ebenen, Lotgerade zu einer Ebene). Der Lotfußpunkt \(F\) des Lotes des Punktes \(P\) auf die Ebene \(E\) ist der Schnittpunkt der Lotgeraden \(\ell\) mit der Ebene \(E\). Der Abstand \(d(P;E)\) des Punktes \(P\) von der Ebene \(E\) ergibt sich als die Länge des Verbindungsvektors \(\overrightarrow{FP}\) bzw. \(\overrightarrow{PF}\).
\[d(P;E) = \overline{FP} = \vert \overrightarrow{FP} \vert\]
Lotgerade \(\ell\) durch \(P\) zur Ebene \(E\) aufstellen:
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]
\(\ell \perp E\), \(P \in \ell\)
\[\Longrightarrow \quad \ell \colon \overrightarrow{X} = \overrightarrow{P} + \lambda \cdot \overrightarrow{n}_{E}; \; \lambda \in \mathbb R\]
Ortsvektor des Lotfußpunktes \(F\) ermitteln (Schnittpunkt der Lotgeraden \(\ell\) mit der Ebene \(E\), vgl. Abiturskript - 2.3.2 Lagebeziehung von Gerade und Ebene, Bestimmung des Schnittpunkts):
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]
\[\ell \colon \overrightarrow{X} = \overrightarrow{P} + \lambda \cdot \overrightarrow{n}_{E}; \; \lambda \in \mathbb R\]
\[\ell \cap E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{P} + \lambda \cdot \overrightarrow{n}_{E} - \overrightarrow{A}) = 0\]
\(\Longrightarrow \quad\)Parameterwert für \(\lambda\)
\(\Longrightarrow \quad\)Ortsvektor \(\overrightarrow{F} \enspace (F \in \ell)\)
Abstand des Punktes \(P\) von der Ebene \(E\) berechnen:
\(d(P;E) = \vert \overrightarrow{FP} \vert\)
Beispielaufgabe
Gegeben sei die Pyramide \(ABCS\) mit der Grundfläche \(ABC\) und der Spitze \(S(1|1|7)\). Die Grundfläche \(ABC\) liegt in der Ebene \(E \colon x_{1} + x_{2} + 3x_{3} - 1 = 0\).
Berechnen Sie die Höhe \(h\) der Pyramide \(ABCS\).
Die Höhe einer Pyramide ist gleich dem Abstand der Spitze der Pyramide von der Ebene, in der die Grundfläche der Pyramide liegt.
\[h = d(S;E)\]
1. Möglichkeit: Hessesche Normalenform der Ebene \(E\) anwenden
\[E \colon x_{1} + x_{2} + 3x_{3} - 1 = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 1 \\ 1 \\ 3 \end{pmatrix}\]
\[S(1|1|7)\]
\[\begin{align*} h &= d(S;E) \\[0.8em] &= \left| \frac{s_{1} + s_{2} + 3s_{3} - 1}{\vert \overrightarrow{n}_{E} \vert} \right| \\[0.8em] &= \left| \frac{1 + 1 + 3 \cdot 7 - 1}{\sqrt{1^{2} + 1^{2} + 3^{2}}} \right| \\[0.8em] &= \frac{22}{\sqrt{11}} \\[0.8em] &= 2\sqrt{11} \\[0.8em] &\approx 6{,}63 \end{align*}\]
2. Möglichkeit: Lotfußpunktverfahren anwenden
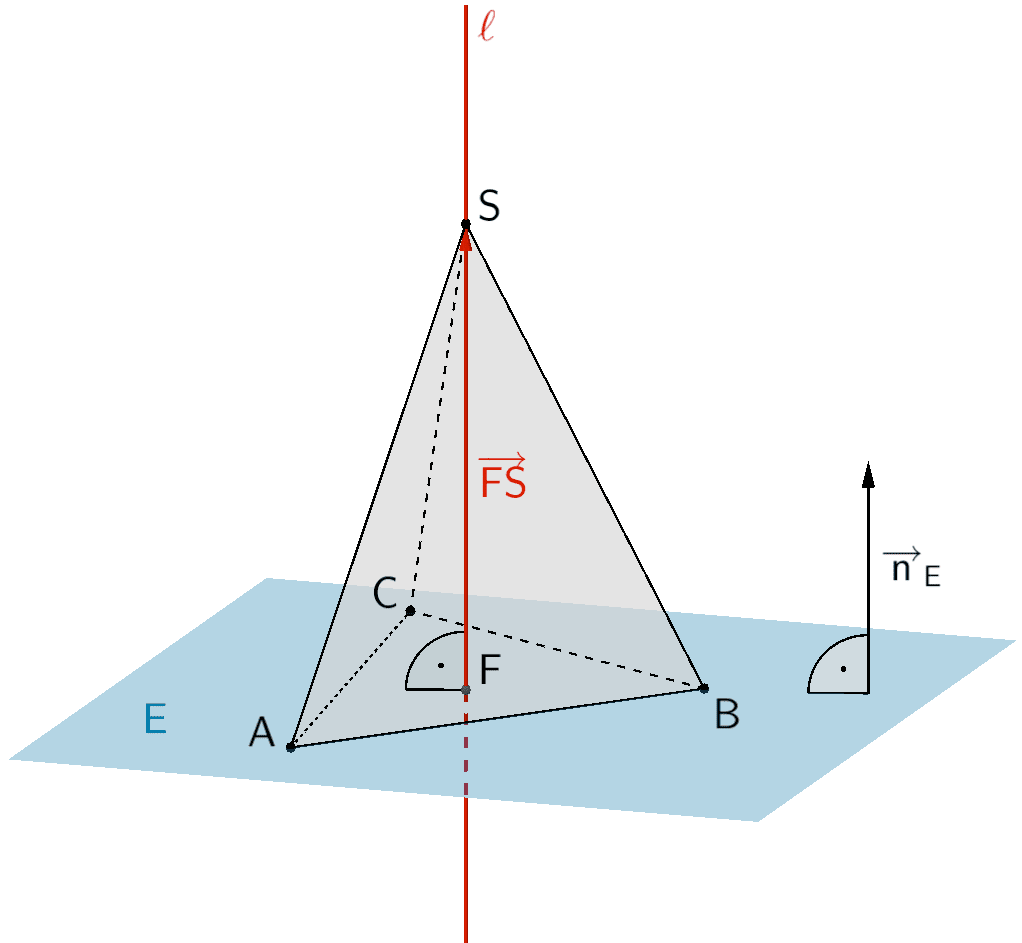
Die Höhe \(h\) der Pyramide \(ABCS\) ist gleich der Länge des Verbindungsvektors \(\overrightarrow{FS}\) zwischenn der Spitze \(S\) und deren Lotpufpunkt \(F\) in der Ebene \(E\).
\[h = d(S;E) = \vert \overrightarrow{FS} \vert\]
Lotgerade \(\ell\) durch \(S\) zur Ebene \(E\) aufstellen (vgl. Abiturskript - 2.3.4 Lotgeraden und orthogonale Ebenen, Lotgerade zu einer Ebene):
\[E \colon x_{1} + x_{2} + 3x_{3} - 1 = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 1 \\ 1 \\ 3 \end{pmatrix}\]
\[S(1|1|7)\]
\(\ell \perp E\), \(S \in \ell\)
\[\ell \colon \overrightarrow{X} = \overrightarrow{S} + \lambda \cdot \overrightarrow{n}_{E}; \; \lambda \in \mathbb R\]
\[\ell \colon \overrightarrow{X} = \begin{pmatrix} 1 \\ 1 \\ 7 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 1 \\ 3 \end{pmatrix}; \; \lambda \in \mathbb R\]
Ortsvektor des Lotfußpunktes \(F\) ermitteln:
Der Lotfußpunkt \(F\) ist der Schnittpunkt der Lotgeraden \(\ell\) mit der Ebene \(E\) (vgl. Abiturskript - 2.3.2 Lagebeziehung von Gerade und Ebene, Bestimmung des Schnittpunkts).
\[E \colon x_{1} + x_{2} + 3x_{3} - 1 = 0\]
\[\ell \colon \overrightarrow{X} = \begin{pmatrix} 1 \\ 1 \\ 7 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 1 \\ 3 \end{pmatrix}; \; \lambda \in \mathbb R\]
\[\begin{align*}\ell \cap E \colon 1 + \lambda + 1 + \lambda + 3 \cdot (7 + 3\lambda) - 1 &= 0 \\[0.8em] 2 + 2\lambda + 21 + 9\lambda - 1 &= 0 \\[0.8em] 22 + 11\lambda &= 0 & &| - 22 \\[0.8em] 11\lambda &= -22 & &| : 11 \\[0.8em] \lambda &= -2 \end{align*}\]
Parameterwert \(\lambda = -2\) in die Gleichung der Lotgeraden \(\ell\) einsetzen:
\[\ell \colon \overrightarrow{X} = \begin{pmatrix} 1 \\ 1 \\ 7 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 1 \\ 3 \end{pmatrix}; \; \lambda \in \mathbb R\]
\[F \in \ell: \overrightarrow{F} = \begin{pmatrix} 1 \\ 1 \\ 7 \end{pmatrix} + (-2) \cdot \begin{pmatrix} 1 \\ 1 \\ 3 \end{pmatrix} = \begin{pmatrix} -1 \\ -1 \\ 1 \end{pmatrix}\]
\[\Longrightarrow \quad {F(-1|-1|1)}\]
Höhe \(h\) der Pyramide \(ABCS\) berechnen:
\(S(1|1|7)\), \(F(-1|-1|1)\)
\[\begin{align*}h = d(S;E) &= \vert \overrightarrow{FS} \vert \\[0.8em] &= \vert \overrightarrow{S} - \overrightarrow{F} \vert \\[0.8em] &= \left| \begin{pmatrix} 1 \\ 1 \\ 7 \end{pmatrix} - \begin{pmatrix} -1 \\ -1 \\ 1 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 2 \\ 2 \\ 6 \end{pmatrix} \right| \\[0.8em] &= \sqrt{2^{2} + 2^{2} + 6^{2}} \\[0.8em] &= \sqrt{44} \\[0.8em] &= 2\sqrt{11} \\[0.8em] &\approx 6{,}63 \end{align*}\]


