Extrem- und Wendepunkte einer Kurvenschar
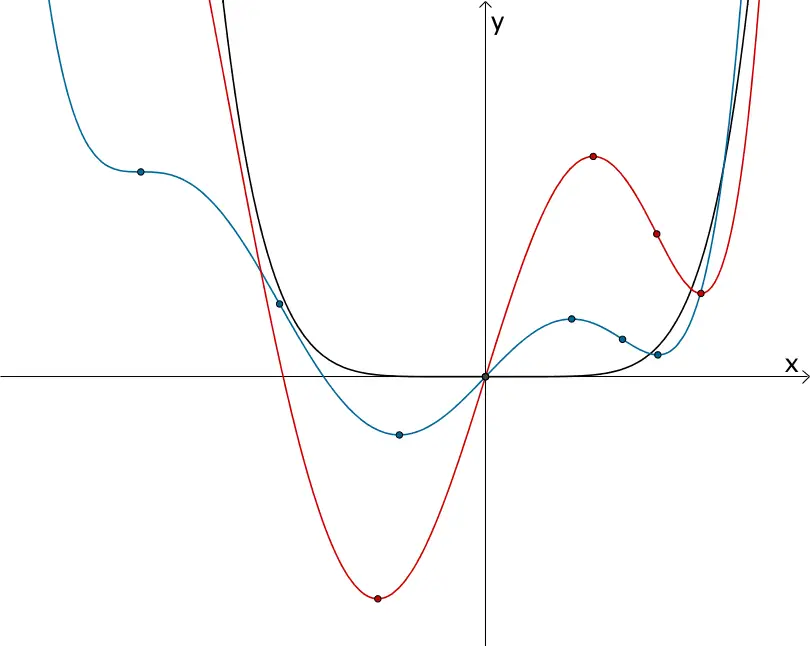
Die Abbildung zeigt für drei verschiedene Werte des Parameters \(k\) die Extrem- und Wendepunkte der zugehörigen Graphen einer ganzrationalen Funktionenschar sechster Ordnung der Form \(f_{k} \colon x \mapsto a_{1}x^{6} + a_{2}kx^{5} + a_{3}k^{2}x^{4} + a_{4}k^{3}x^{3} + a_{5}k^{4}x^{2} + a_{6}k^{5}x\) (vgl. Abiturskript - 1.1.3 Ganzrationale Funktion).
Es wird deutlich, dass die Anzahl sowie die Lage und die Art der Extrem- und Wendepunkte vom Wert des Parameters \(k\) maßgeblich bestimmt werden.
Vorgehensweise - Extrem- und Wendepunkte einer Kurvenschar
Die möglichen Extrem- bzw. Wendestellen einer Funktionenschar \(f_{k}\) werden zunächst, wie in den Kapiteln Abiturskript - 1.5.3 Monotonieverhalten, Extrem- und Terrassenpunkte bzw. Abiturskript - 1.5.4 Krümmungsverhalten und Wendepunkte beschrieben, ermittelt und in Abhängigkeit des Parameters \(k\) formuliert.
Anschließend gilt es zu überprüfen, für welche Werte des Parameters \(k\) tatsächlich eine Extremstelle bzw. eine Wendestelle vorliegt, von welcher Art diese ist und ob ggf. die Vorraussetzungen für einen Terrassenpunkt erfüllt sind.
Beispiel:
Gegeben sei die in \(\mathbb R\) definierte Funktionenschar \(f_{k} \colon x \mapsto \frac{1}{6} \left( x^{3} -2kx^{2} + k^{2}x \right)\) mit \(k \in \mathbb R_{0}^{+}\).
Ermitteln Sie in Abhängigkeit des Parameters \(k\) die Lage und die Art der Extrem- und Wendepunkte der Kurvenschar von \(f_{k}\).
\[f_{k}(x) = \frac{1}{6}\left( x^{3} - 2kx^{2} + k^{2}x \right); \; D_{f_{k}} = \mathbb R, \; k \in \mathbb R_{0}^{+}\]
Extrempunkte der Kurvenschar der Funktionenschar \(f_{k}\)
Die notwendige Bedingung für eine Extremstelle der Funktionenschar \(f_{k}\) lautet: \(f'_{k}(x) = 0\) (vgl. Abiturskript - 1.5.3 Monotonieverhalten, Extrem- und Terrassenpunkte).
Erste Ableitung \(f'_{k}\) bilden:
Die Ableitung des Funktionsterms \(f_{k}(x)\) kann unter Beachtung der Faktor- und der Summenregel und mithilfe der Ableitung einer Potenzfunktion erfolgen. Der Parameter \(k\) wird beim Ableiten wie eine Konstante behandelt (vgl. Abiturskript - 1.5.2 Ableitungsregeln).
\[f_{k}(x) = \frac{1}{6}\left( x^{3} - 2kx^{2} + k^{2}x \right)\]
\[\begin{align*} f'_{k}(x) &= \frac{1}{6}\left( 3 \cdot x^{2} - 2k \cdot 2 \cdot x +k^{2} \right) \\[0.8em] &= \frac{1}{6}\left( 3x^{2} - 4kx + k^{2} \right) \end{align*}\]
Nullstellen von \(f'_{k}\) bestimmen:
\[f'_{k}(x) = 0 \quad \Longrightarrow \quad 3x^{2} - 4kx + k^{2} = 0\]
Lösungsformel für quadratische Gleichungen anwenden (vgl. Abiturskript - 1.1.2 Quadratische Funktion, Lösungsformel für quadratische Gleichungen, vgl. Merkhilfe):
\[\begin{align*} x_{1,2} &= \frac{4k \pm \sqrt{(-4k)^{2} - 4 \cdot 3 \cdot k^{2}}}{2 \cdot 3} \\[0.8em] &= \frac{4k \pm \sqrt{16k^{2} - 12k^{2}}}{6} \\[0.8em] &= \frac{4k \pm 2k}{6} \\[0.8em] &= \frac{2}{3}k \pm \frac{1}{3}k \end{align*}\]
\[x_{1} = \frac{2}{3}k - \frac{1}{3}k = \frac{1}{3}k\]
\[x_{2} = \frac{2}{3}k + \frac{1}{3}k = k\]
An den Stellen \(x_{1} = \frac{1}{3}k\) und \(x_{2} = k\) mit \(k \in \mathbb R_{0}^{+}\) besitzt die Kurvenschar der Funktionenschar \(f_{k}\) waagrechte Tangenten.
Nun ist zu untersuchen, für welche Werte des Parameters \(k\) die Stellen \(x_{1}\) und \(x_{2}\) einfache Nullstellen von \(f'_{k}\) sind, das heißt Nullstellen mit Vorzeichenwechsel, welche Extremstellen bestätigen.
Und es ist zu prüfen, ob es ggf. einen Wert \(k \in \mathbb R_{0}^{+}\) gibt, sodass mit \(x_{1} = x_{2}\) eine doppelte Nullstelle von \(f'_{k}\) ohne Vorzeichenwechsel vorliegt, welche auf einen Terrassenpunkt verweist.
(vgl. Abiturskript - 1.5.3 Monotonieverhalten, Extrem- und Terrassenpunkte)
Es ergibt sich folgende Fallunterscheidung:
\[x_{1} = \frac{1}{3}k; \enspace x_{2} = k\]
\[f'_{k}(x) = \frac{1}{6}\left( 3x^{2} - 4kx + k^{2} \right)\]
1. Fall: \(k = 0\)
\[x_{1} = \frac{1}{3} \cdot 0 = 0\]
\[x_{2} = 0\]
\[\Longrightarrow \quad x_{1} = x_{2} = 0\]
\(\Longrightarrow \quad\) doppelte Nullstelle \(x = 0\) (ohne Vorzeichenwechsel) für \(k = 0\)
Aus der doppelten Nullstelle \(x = 0\) für \(k = 0\) lässt sich mithilfe des Monotoniekriteriums schlussfolgern, dass der Graph der Scharfunktion \(f_{0}\) an der Stelle \(x = 0\) einen Terrassenpunkt hat (vgl. Abiturskript - 1.5.3 Monotonieverhalten, Extrem- und Terrassenpunkte).
\[f'_{k}(x) = \frac{1}{6}\left( 3x^{2} - 4kx + k^{2} \right)\]
\[f'_{0}(x) = \underbrace{\frac{1}{2}x^{2}}_{>\,0}\]
\[f'_{0}(0) = \frac{1}{2} \cdot 0^{2} = 0\]
In der Umgebung der doppelten Nullstelle \(x = 0\) für \(k = 0\) gilt stets \(f'_{0} > 0\). Der Graph der Scharfunktion \(f_{2}\) ist damit in der Umgebung von \(x = 0\) streng monoton steigend. Folglich besitzt er an der Stelle \(x = 0\) einen Terrassenpunkt.
\[\left. \begin{align*} f'_{0}(0) &= 0 \\[0.8em] f'_{0}(x) &> 0 \; \text{für} \; x < 0 \\[0.8em] f'_{0}(x) &> 0 \; \text{für} \; x > 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Terrassenpunkt}\; TeP (0|f_{0}(0))\]
Veranschaulichung mithilfe einer Monotonietabelle:
| \(x < 0\) | \(x = 0\) | \(x > 0\) | |
| \(f'_{0}(x) = \frac{1}{2} x^{2}\) | \(+\) | \(0\) | \(+\) |
| \(G_{f_{0}}\) | \(\nearrow\) | \(TeP(0|f_{0}(0))\) | \(\nearrow\) |
Als Alternative bietet sich der Nachweis des Terrassenpunkts mithilfe der zweiten Ableitung \(f''_{0}\) oder mithilfe der dritten Ableitung \(f'''_{0}\) an (vgl. Abiturskript - 1.5.4 Krümmungsverhalten und Wendepunkte, Terrassenpunkte). Die Ableitungen erfolgen wiederum unter Beachtung der Faktor- und der Summenregel und mithilfe der Ableitung einer Potenzfunktion. Der Parameter \(k\) wird beim Ableiten wie eine Konstante behandelt (vgl. Abiturskript - 1.5.2 Ableitungsregeln).
\[f'_{k}(x) = \frac{1}{6}\left( 3x^{2} - 4kx + k^{2} \right)\]
\[f'_{0}(x) = \frac{1}{2}x^{2}\]
\[f'_{0}(0) = \frac{1}{2} \cdot 0^{2} = 0\]
\[\begin{align*}f''_{k}(x) &= \frac{1}{6}\left( 2 \cdot 3x - 4k + 0 \right) \\[0.8em] &= \frac{1}{6}(6x - 4k) \\[0.8em] &= x - \frac{2}{3}k \end{align*}\]
\[f''_{0}(x) = x - \frac{2}{3} \cdot 0 = x\]
\[f''_{0}(0) = 0\]
\[f'''_{k}(x) = 1\]
\[f'''_{0}(x) = 1\]
\[f'''_{0}(0) = 1 \neq 0\]
Begründung des Terrassenpunkts mithilfe des Vorzeichenwechsels von \(f''_{0}\):
\[\left. \begin{align*} f'_{0}(0) &= 0 \\[0.8em] f''_{2}(0) &= 0 \\[0.8em] f''_{0}(x) &< 0 \; \text{für} \; x < 0 \\[0.8em] f''_{0}(x) &> 0 \; \text{für} \; x > 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Terrassenpunkt}\; TeP (0|f_{0}(0))\]
Begründung des Terrassenpunkts mithilfe der dritten Ableitung \(f'''_{0}\):
\[\left. \begin{align*} f'_{0}(0) &= 0 \\[0.8em] f''_{2}(0) &= 0 \\[0.8em] f'''_{0}(0) &\neq 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Terrassenpunkt}\; TeP (0|f_{0}(0))\]
Lage (Koordinaten) des Terrassenpunkts:
\[f_{k}(x) = \frac{1}{6}\left( x^{3} - 2kx^{2} + k^{2}x \right)\]
\[f_{0}(x) = \frac{1}{6}\left( x^{3} - 2 \cdot 0 \cdot x^{2} + 0^{2}x \right) = \frac{1}{6}x^{3}\]
\[f_{0}(0) = \frac{1}{6} \cdot 0^{3} = 0\]
\(\Longrightarrow \quad\)Terrassenpunkt \(TeP(0|0)\)
Für \(k = 0\) besitzt der Graph der Scharfunktion \(f_{0}\) an der Stelle \(x = 0\) den Terrassenpunkt \(TeP(0|0)\).
2. Fall: \(k > 0\)
\[x_{1} = \frac{1}{3}k; \enspace x_{2} = k\]
\[f'_{k}(x) = \frac{1}{6}\left( 3x^{2} - 4kx + k^{2} \right)\]
Für \(k > 0\) besitzt die erste Ableitung \(f'_{k}\) an den Stellen \(x_{1} = \frac{1}{3}k\) und \(x_{2} = k\) jeweils eine einfache Nullstelle mit Vorzeichenwechsel. Das bedeutet, dass die Kurvenschar an den Stellen \(x_{1}\) und \(x_{2}\) jeweils das Monotonieverhalten ändert, was Extremstellen bestätigt.
Der Nachweis der Art der Extremstellen \(x_{1} = \frac{1}{3}k\) und \(x_{2} = k\) für \(k > 0\) kann mithilfe des Monotoniekriteriums oder mithilfe des Vorzeichens der zweiten Ableitung \(f''_{k}\) an den Stellen \(x_{1}\) und \(x_{2}\) erfolgen (vgl. Abiturskript - 1.5.3 Monotonieverhalten, Extrem- und Terrassenpunkte).
1. Nachweis der Art der Extremstellen mithilfe des Monotoniekriteriums
Um den Vorzeichenwechsel der ersten Ableitung \(f'_{k}\) an deren Nullstellen \(x_{1}\) und \(x_{2}\) besser erkennen und dokumentieren zu können, ist es zweckmäßig, den Funktionsterm \(f'_{k}(x)\) zu faktorisieren. Die Nullstellen \(x_{1} = \frac{1}{3}k\) und \(x_{2} = k\) legen die Linearfaktoren \((x - \frac{1}{3}k)\) und \((x - k)\) fest. (vgl. Abiturskript - 1.1.2 Quadratische Funktion, Produktform und Linearfaktorzerlegung).
Damit lässt sich der Funktionsterm \(f'_{k}(x)\) wie folgt in der Produktform angeben:
\[\begin{align*} f'_{k}(x) &= \frac{1}{6}\left( 3x^{2} - 4kx + k^{2} \right) \\[0.8em] &= \frac{1}{6} \cdot 3 \cdot \left( x^{2} - \frac{4}{3}kx + \frac{1}{3}k^{2} \right) \\[0.8em] &= \frac{1}{2}\left(x - \frac{1}{3}k \right)(x - k) \end{align*}\]
Art der Extremstellen \(x_{1} = \frac{1}{3}k\):
\[\left. \begin{align*} &\textstyle f'_{k}\left( \frac{1}{3}k \right) = 0 \\[0.8em] &f'_{k}(x) > 0 \; \text{für} \; \textstyle x < \frac{1}{3}k \\[0.8em] &f'_{k}(x) < 0 \; \text{für} \; \textstyle x > \frac{1}{3}k \end{align*} \right\} \enspace \Rightarrow \enspace \text{Hochpunkte}\; \textstyle HoP\left(\small{\frac{1}{3}k}\,\Big|\,f_{k}\left( \frac{1}{3}k \right) \right) \]
Veranschaulichung mithilfe einer Monotonietabelle:
| \((k > 0)\) | \(x < \frac{1}{3}k\) | \(x = \frac{1}{3}k\) | \(x > \frac{1}{3}k\) |
| \(\left( x - \frac{1}{3}k \right)\) | \(-\) | \(0\) | \(+\) |
| \((x - k)\) | \(-\) | \(-\) | \(-\) |
| \(f'_{k}(x)\) | \(+\) | \(0\) | \(-\) |
| \(G_{f_{k}}\) | \(\nearrow\) | \(HoP \left(\frac{1}{3}k\, \Big|\, f_{k}\left(\frac{1}{3}k \right) \right)\) | \(\searrow\) |
Art der Extremstellen \(x_{2} = k\):
\[\left. \begin{align*} &f'_{k}(k) = 0 \\[0.8em] &f'_{k}(x) < 0 \; \text{für} \; x < k \\[0.8em] &f'_{k}(x) > 0 \; \text{für} \; x > k \end{align*} \right\} \enspace \Rightarrow \enspace \text{Tiefpunkte}\; TiP(k| f_{k}(k))\]
Veranschaulichung mithilfe einer Monotonietabelle:
| \((k > 0)\) | \(x < k\) | \(x = k\) | \(x > k\) |
| \(\left( x - \frac{1}{3}k \right)\) | \(+\) | \(+\) | \(+\) |
| \((x - k)\) | \(-\) | \(0\) | \(+\) |
| \(f'_{k}(x)\) | \(-\) | \(0\) | \(+\) |
| \(G_{f_{k}}\) | \(\searrow\) | \(TiP(k| f_{k}(k))\) | \(\nearrow\) |
2. Nachweis der Art der Extremstellen mithilfe der zweiten Ableitung
(vgl. Abiturskript - 1.5.3 Monotonieverhalten, Extrem- und Terrassenpunkte)
\[f'_{k}(x) = \frac{1}{2}\left(x - \frac{1}{3}k \right)(x - k)\]
\(f''_{k}(x) = x - \dfrac{2}{3}k\) (vgl. oben)
Art der Extremstellen \(x_{1} = \frac{1}{3}k\):
\[f''_{k}\left( \textstyle \frac{1}{3}k \right) = \frac{1}{3}k - \frac{2}{3}k = -\frac{1}{3}k; \; (k > 0)\]
\[\left. \begin{align*} &f'_{k}\left( \textstyle \frac{1}{3}k \right) = 0 \\[0.8em] &f''_{k}\left( \textstyle \frac{1}{3}k \right) < 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Hochpunkte} \; HoP\left(\textstyle \frac{1}{3}k \, \Big| \, f_{k}\left( \textstyle \frac{1}{3}k \right) \right)\]
Art der Extremstellen \(x_{2} = k\):
\[f''_{k}(k) = k - \frac{2}{3}k = \frac{1}{3}k; \; (k > 0)\]
\[\left. \begin{align*} &f'_{k}(k) = 0 \\[0.8em] &f''_{k}(k) > 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Tiefpunkte} \; TiP(k| f_{k}(k))\]
Lage (Koordinaten) der Extremstellen:
\[HoP\left(\textstyle \frac{1}{3}k \, \Big| \, f_{k}\left( \textstyle \frac{1}{3}k \right) \right)\]
\[TiP(k|f_{k}(k))\]
\[f_{k}(x) = \frac{1}{6}\left( x^{3} - 2kx^{2} + k^{2}x \right)\]
\[\begin{align*} f_{k}\left( \textstyle \frac{1}{3}k \right) &= \frac{1}{6}\left( \left( \frac{1}{3}k \right)^{3} - 2k \cdot \left( \frac{1}{3}k \right)^{2} + k^{2} \cdot \frac{1}{3}k \right) \\[0.8em] &= \frac{1}{6}\left( \frac{1}{27}k^{3} - \frac{2}{9}k^{3} + \frac{1}{3}k^{3} \right) \\[0.8em] &= \frac{1}{6}\left( \frac{1}{27}k^{3} - \frac{6}{27}k^{3} + \frac{9}{27}k^{3} \right) \\[0.8em] &= \frac{1}{6} \cdot \frac{4}{27}k^{3} \\[0.8em] &= \frac{2}{81}k^{3} \end{align*}\]
\[\Longrightarrow \quad HoP\left(\textstyle \frac{1}{3}k \, \Big| \, \textstyle \frac{2}{81}k^{3} \right)\]
\[\begin{align*} f_{k}(k) &= \frac{1}{6}\left( k^{3} - 2k \cdot k^{2} + k^{2} \cdot k \right) \\[0.8em] &= \frac{1}{6}\left( k^{3} - 2k^{3} + k^{3} \right) \\[0.8em] &= 0 \end{align*}\]
\[\Longrightarrow \quad TiP(k|0)\]
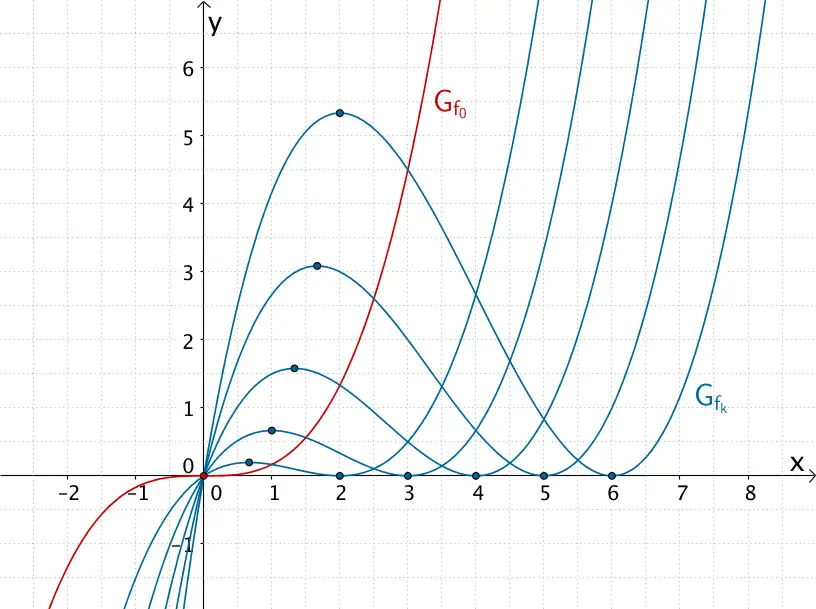
Extrempunkte der Kurvenschar \(G_{f_{k}}\) der Funktionenschar \(f_{k} \colon x \mapsto \frac{1}{6}\left( x^{3} -2kx^{2} + k^{2}x \right)\) für \(k > 0\) und Terrassenpunkt des Graphen \(G_{f_{0}}\) der Scharfunktion \(f_{0} \colon x \mapsto \frac{1}{6}x^{3}\) für \(k = 0\)
Wendepunkte der Kurvenschar der Funktionenschar \(f_{k}\)
Die Bestimmung der Extrempunkte der Funktionenschar \(f_{k}\) hat bereits ergeben, dass für \(k = 0\) der Graph \(G_{f_{0}}\) der Scharfunktion \(f_{0}\) den Terrassenpunkt \(TeP(0|0)\) besitzt. Somit verbleibt die Untersuchung der Wendepunkte für den Fall \(k > 0\) (vgl. Abiturskript - 1.5.4 Krümmungsverhalten und Wendepunkte).
\(f''_{k}(x) = x - \dfrac{2}{3}k\) (vgl. oben)
Nullstelle(n) von \(f''_{k}\) bestimmen:
\[\begin{align*}f''_{k}(x) &= 0 \\[0.8em] x - \frac{2}{3}k &= 0 & &| + \frac{2}{3}k \\[0.8em] x = \frac{2}{3}k \end{align*}\]
Für \(k > 0\) sind die Stellen \(x = \frac{2}{3}k\) mögliche Wendestellen der Kurvenschar von \(f_{k}\).
Begründung der Wendestellen mithilfe des Vorzeichenwechsels von \(f''_{k}\):
\[\left. \begin{align*} f''_{k}\left( \textstyle \frac{2}{3}k \right) = 0 \\[0.8em] f''_{k}(x) < 0 \; \text{für} \, x < \textstyle \frac{2}{3}k \\[0.8em] f''_{k}(x) > 0 \; \text{für} \; x > \textstyle \frac{2}{3}k \end{align*} \right\} \enspace \Rightarrow \enspace \text{Wendepunkte} \; W\left(\textstyle \frac{2}{3}k \, \Big| \, f_{k}\left( \textstyle \frac{2}{3}k \right) \right)\]
Veranschaulichung mithilfe einer Krümmungstabelle:
| \((k > 0)\) | \(x < \frac{2}{3}k\) | \(x = \frac{2}{3}k\) | \(x > \frac{2}{3}k\) |
| \(f''_{k}(x)\) | \(-\) | \(0\) | \(+\) |
| \(G_{f_{k}}\) | \(\Large \curvearrowright\) | \(W\left(\textstyle \frac{2}{3}k \, \Big| \, f_{k}\left( \textstyle \frac{2}{3}k \right) \right)\) | \(\style{display: inline-block; transform:rotate(0.5turn);}{\Large \curvearrowleft}\) |
Begründung der Wendestellen mithilfe der dritten Ableitung \(f'''_{k}\):
\(f'''_{k}(x) = 1\) (vgl. oben)
\[\left. \begin{align*} &f''_{k}\left( \textstyle \frac{2}{3}k \right) = 0 \\[0.8em] &f'''_{k}\left( \textstyle \frac{2}{3}k \right) \neq 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Wendepunkte} \; W\left(\textstyle \frac{2}{3}k \, \Big| \, f_{k}\left( \textstyle \frac{2}{3}k \right) \right)\]
Lage (Koordinaten) der Wendestellen:
\[W\left(\textstyle \frac{2}{3}k \, \Big| \, f_{k}\left( \textstyle \frac{2}{3}k \right) \right)\]
\[f_{k}(x) = \frac{1}{6}\left( x^{3} - 2kx^{2} + k^{2}x \right)\]
\[\begin{align*} f_{k}\left( \textstyle \frac{2}{3}k \right) &= \frac{1}{6}\left( \left( \frac{2}{3}k \right)^{3} - 2k \cdot \left( \frac{2}{3}k \right)^{2} + k^{2} \cdot \frac{2}{3}k \right) \\[0.8em] &= \frac{1}{6}\left( \frac{8}{27}k^{3} - \frac{8}{9}k^{3} + \frac{2}{3}k^{3} \right) \\[0.8em] &= \frac{1}{6}\left( \frac{8}{27}k^{3} - \frac{24}{27}k^{3} + \frac{18}{27}k^{3} \right) \\[0.8em] &= \frac{1}{6} \cdot \frac{2}{27}k^{3} \\[0.8em] &= \frac{1}{81}k^{3} \end{align*}\]
\[\Longrightarrow \quad W\left(\textstyle \frac{2}{3}k \, \Big| \, \textstyle \frac{1}{81}k^{3} \right)\]
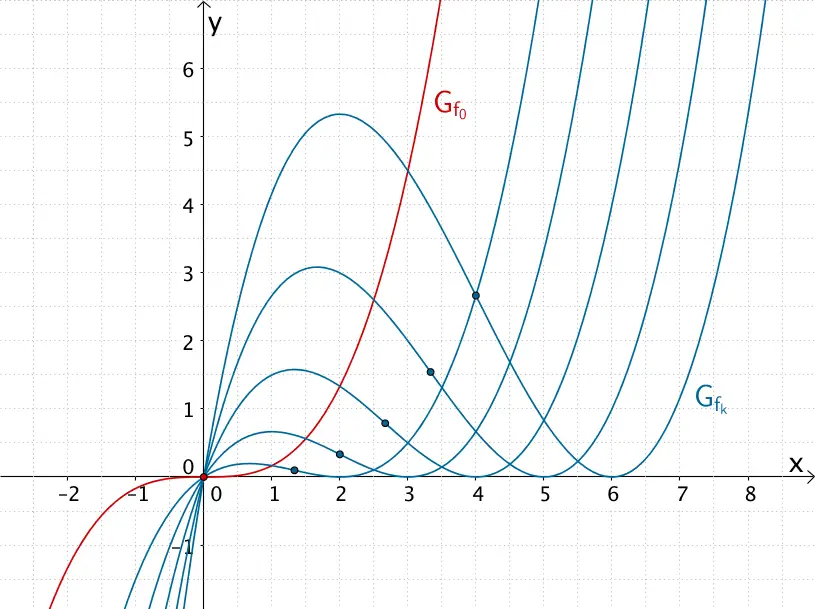
Wendepunkte der Kurvenschar \(G_{f_{k}}\) der Funktionenschar \(f_{k} \colon x \mapsto \frac{1}{6}\left( x^{3} -2kx^{2} + k^{2}x \right)\) für \(k > 0\) und Terrassenpunkt des Graphen \(G_{f_{0}}\) der Scharfunktion \(f_{0} \colon x \mapsto \frac{1}{6}x^{3}\) für \(k = 0\)
Orthogonale Wendetangenten
Betrachtet wird die Kurvenschar \(G_{f_{k}}\) einer Funktionenschar \(f_{k}\), welche für bestimmte Werte des Parameters \(k\) zwei Wendepunkte \(W_{1}\) und \(W_{2}\) mit den Wendetangenten \(w_{1}\) und \(w_{2}\) besitzt. Für welchen Wert des Parameters \(k\) sind die beiden Wendetangenten orthogonal (zueinander senkrecht)?
Für die Steigungen \(m_{1}\) und \(m_{2}\) zweier zueinander senkrechter Geraden gilt: \(m_{1} \cdot m_{2} = -1 \enspace \Leftrightarrow \enspace m_{1} = -\dfrac{1}{m_{2}}\) (vgl. Abiturskript - 1.1.1 Lineare Funktion, Steigung einer Geraden)
Die erste Ableitung \(f'_{k}\) der Funktionenschar \(f_{k}\) beschreibt die Steigungen \(m_{w_{1}}\) und \(m_{w_{2}}\) der Wendetangenten \(w_{1}\) und \(w_{2}\) an den Wendestellen \(x_{1}\) bzw. \(x_{2}\) (vgl. Abiturskript - 1.5.1 Die Ableitung, Tangentensteigung).
Somit ergibt sich folgender Ansatz:
\[\begin{align*} m_{w_{1}} &= -\frac{1}{m_{w_{2}}} \\[0.8em] f'_{k}(x_{1}) &= -\frac{1}{f'_{k}(x_{2})} \end{align*}\]
Vorgehensweise
In einem ersten Schritt werden die Wendestellen der Funktionenschar \(f_{k}\) in Abhängigkeit des Parameters \(k\) bestimmt (vgl. 1.7.5 - Seite 1 Extrem- und Wendepunkte einer Kurvenschar bzw. Abiturskript - 1.5.4 Krümmungsverhalten und Wendepunkte). Anschließend ist zu überprüfen, für welche Werte des Parameters \(k\) zwei (verschiedene) Wendestellen vorliegen.
Die Lösung der Gleichung \(f'_{k}(x_{1}) = -\dfrac{1}{f'_{k}(x_{2})}\) liefert schließlich den gesuchten Wert des Parameters \(k\), sodass die Wendetangenten zueinander senkrecht sind.
Beispiel:
Gegeben sei die in \(\mathbb R\) definierte Funktionenschar \(f_{k} \colon x \mapsto 0{,}5kx^{4} - 4kx^{2}\) mit \(k > 0\).
Für welchen Wert des Parameters \(k\) hat der zugehörige Graph der Funktionenschar \(f_{k}\) zwei zueinander senkrechte Wendetangenten?
\[f_{k}(x) = 0{,}5kx^{4} - 4kx^{2}; \; D_{f_{k}} = \mathbb R, \; k > 0\]
Ableitungen \(f'_{k}\), \(f''_{k}\) und \(f'''_{k}\) bilden:
Mit der ersten Ableitung \(f'_{k}\) werden die Steigungen der Wendetangenten beschrieben (vgl. Ansatz oben). Mithilfe der zweiten Ableitung \(f''_{k}\) lassen sich die Wendestellen bestimmen. Die dritte Ableitung \(f'''_{k}\) dient optional für den Nachweis der Wendestellen (vgl. Abiturskript - 1.5.4 Krümmungsverhalten und Wendepunkte). Die Funktionsterme \(f_{k}(x)\), \(f'_{k}(x)\) und \(f''_{k}(x)\) können unter Beachtung der Faktor- und der Summenregel sowie mithilfe der Ableitung einer Potenzfunktion abgeleitet werden. Der Parameter \(k\) wird dabei wie eine Konstante behandelt (vgl. Abiturskript - 1.5.2 Ableitungsregeln).
\[f_{k}(x) = 0{,}5kx^{4} - 4kx^{2}; \; D_{f_{k}}\]
\[\begin{align*}f'_{k}(x) &= 0{,}5k \cdot 4 \cdot x^{3} - 4k \cdot 2 \cdot x \\[0.8em] &= 2kx^{3} - 8kx \end{align*}\]
\[\begin{align*}f''_{k}(x) &= 2k \cdot 3 \cdot x^{2} - 8k \\[0.8em] &= 6kx^{2} - 8k \end{align*}\]
\[\begin{align*} f'''_{k}(x) &= 6k \cdot 2 \cdot x - 0 \\[0.8em] &= 12kx \end{align*}\]
Wendestellen der Funktionenschar \(f_{k}\) ermitteln:
Die Nullstellen von \(f''_{k}\) sind mögliche Wendestellen (vgl. Abiturskript - 1.5.4 Krümmungsverhalten und Wendepunkte).
\[\begin{align*} f''_{k}(x) &= 0 \\[0.8em] 6kx^{2} - 8k &= 0 & &| + 8k \\[0.8em] 6kx^{2} &= 8k & &| : 6k \\[0.8em] x^{2} &= \frac{4}{3} & &| \; \sqrt{\quad} \\[0.8em] x_{1,2} &= \pm \frac{2}{\sqrt{3}} \\[0.8em] &= \pm \frac{2\sqrt{3}}{3} \end{align*}\]
Unabhängig vom Wert des Paraments \(k\) sind \(x_{1} = -\frac{2\sqrt{3}}{3}\) und \(x_{2} = \frac{2\sqrt{3}}{3}\) mögliche Wendestellen der Funktionenschar \(f_{k}\).
Nachweis der Wendestellen \(x_{1}\) und \(x_{2}\):
Die Begründung der Wendestellen kann mithilfe des Vorzeichenwechsels von \(f''_{k}\) oder mithilfe der dritten Ableitung \(f'''_{k}\) erfolgen (vgl. Abiturskript - 1.5.4 Krümmungsverhalten und Wendepunkte).
Begründung mithilfe des Vorzeichenwechsels von \(f''_{k}\):
Der Vorzeichenwechsel von \(f''_{k}\) an den Stellen \(x_{1} = -\frac{2\sqrt{3}}{3}\) und \(x_{2} = \frac{2\sqrt{3}}{3}\) lässt sich besser beurteilen, wenn der Funktionsterm \(f''_{k}(x)\) in der Produktform vorliegt. Unter Berücksichtigung der Nullstellen \(x_{1}\) und \(x_{2}\) von \(f''_{k}\) sowie der 3. Binomischen Formel wird der Funktionsterm \(f''_{k}(x)\) faktorisiert.
\[\begin{align*} f''_{k}(x) &= 6kx^{2} - 8k \\[0.8em] &= 6k \bigg( \underbrace{x^{2} - \frac{4}{3}}_{\large{a^{2}\,-\,b^{2}}} \bigg) \\[0.8em] &= 6k \underbrace{\left( x - \frac{2\sqrt{3}}{3} \right) \left( x + \frac{2\sqrt{3}}{3} \right)}_{\large{(a\,-\,b)(a\,+\,b)}} \enspace (k > 0) \end{align*}\]
\[\left. \begin{align*} &f''_{k}\left( \textstyle -\frac{2\sqrt{3}}{3} \right) = 0 \\[0.8em] &f''_{k}(x) > 0 \; \text{für} \; x < \textstyle -\frac{2\sqrt{3}}{3} \\[0.8em] &f''_{k}{x} < 0 \, \text{für} \; x > \textstyle -\frac{2\sqrt{3}}{3} \end{align*} \right\} \enspace \Rightarrow \enspace \text{Wendepunkte}\; W_{1}\left(\textstyle -\frac{2\sqrt{3}}{3} \, \Big| \, f_{k}\left( \textstyle -\frac{2\sqrt{3}}{3} \right) \right)\]
\[\left. \begin{align*} &f''_{k}\left( \textstyle \frac{2\sqrt{3}}{3} \right) = 0 \\[0.8em] &f''_{k}(x) < 0 \; \text{für} \; x < \textstyle \frac{2\sqrt{3}}{3} \\[0.8em] &f''_{k}{x} > 0 \, \text{für} \; x > \textstyle \frac{2\sqrt{3}}{3} \end{align*} \right\} \enspace \Rightarrow \enspace \text{Wendepunkte}\; W_{2}\left(\textstyle \frac{2\sqrt{3}}{3} \, \Big| \, f_{k}\left( \textstyle \frac{2\sqrt{3}}{3} \right) \right)\]
Veranschaulichung mithilfe einer Krümmungstabelle:
| \((k > 0)\) | \(x < -\frac{2\sqrt{3}}{3}\) | \(x = -\frac{2\sqrt{3}}{3}\) | \(x > -\frac{2\sqrt{3}}{3}\) |
| \(6k\) | \(+\) | \(+\) | \(+\) |
| \(\left(x - \frac{2\sqrt{3}}{3} \right)\) | \(-\) | \(-\) | \(-\) |
| \(\left( x + \frac{2\sqrt{3}}{3} \right)\) | \(-\) | \(0\) | \(+\) |
| \(f''_{k}(x)\) | \(+\) | \(0\) | \(-\) |
| \(G_{f_{k}}\) | \(\style{display: inline-block; transform:rotate(0.5turn);}{\Large \curvearrowleft}\) | \(W_{1}\left(-\frac{2\sqrt{3}}{3}\, \Big| \, f_{k}\left( -\frac{2\sqrt{3}}{3} \right) \right)\) | \(\Large \curvearrowright\) |
| \((k > 0)\) | \(x < \frac{2\sqrt{3}}{3}\) | \(x = \frac{2\sqrt{3}}{3}\) | \(x > \frac{2\sqrt{3}}{3}\) |
| \(6k\) | \(+\) | \(+\) | \(+\) |
| \(\left(x - \frac{2\sqrt{3}}{3} \right)\) | \(-\) | \(0\) | \(+\) |
| \(\left( x + \frac{2\sqrt{3}}{3} \right)\) | \(+\) | \(+\) | \(+\) |
| \(f''_{k}(x)\) | \(-\) | \(0\) | \(+\) |
| \(G_{f_{k}}\) | \(\Large \curvearrowright\) | \(W_{2}\left(\frac{2\sqrt{3}}{3}\, \Big| \, f_{k}\left( \frac{2\sqrt{3}}{3} \right) \right)\) | \(\style{display: inline-block; transform:rotate(0.5turn);}{\Large \curvearrowleft}\) |
Begründung mithilfe der dritten Ableitung \(f'''_{k}\):
\(f'''_{k}(x) = 12kx\) (vgl. oben)
\[k > 0\]
\[\left. \begin{align*} &f''_{k}\left( \textstyle -\frac{2\sqrt{3}}{3} \right) = 0 \\[0.8em] &f'''_{k}\left( \textstyle -\frac{2\sqrt{3}}{3} \right) \neq 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Wendepunkte}\; W_{1}\left(\textstyle -\frac{2\sqrt{3}}{3} \, \Big| \, f_{k}\left( \textstyle -\frac{2\sqrt{3}}{3} \right) \right)\]
\[\left. \begin{align*} &f''_{k}\left( \textstyle \frac{2\sqrt{3}}{3} \right) = 0 \\[0.8em] &f'''_{k}\left( \textstyle \frac{2\sqrt{3}}{3} \right) \neq 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Wendepunkte}\; W_{2}\left(\textstyle \frac{2\sqrt{3}}{3} \, \Big| \, f_{k}\left( \textstyle \frac{2\sqrt{3}}{3} \right) \right)\]
Die Funktionenschar \(f_{k}\) besitzt die Wendestellen \(x_{1} = -\frac{2\sqrt{3}}{3}\) und \(x_{2} = \frac{2\sqrt{3}}{3}\).
Wert des Parameters \(k\) für orthogonale Wendetangenten berechnen:
\[x_{1} = -\frac{2\sqrt{3}}{3}; \enspace x_{2} = \frac{2\sqrt{3}}{3}\]
\(f'_{k}(x) = 2kx^{3} - 8kx\) (vgl. oben)
\[f'_{k}(x_{1}) = -\frac{1}{f'_{k}(x_{2})}\]
\[\begin{align*}f'_{k}(x_{1}) &= f'_{k}\left( \textstyle -\frac{2\sqrt{3}}{3} \right) \\[0.8em] &= 2k \cdot \left( -\frac{2\sqrt{3}}{3} \right)^{3} - 8k \cdot \left( -\frac{2\sqrt{3}}{3} \right) \\[0.8em] &= -\frac{48\sqrt{3}}{27}k + \frac{16\sqrt{3}}{3}k \\[0.8em] &= -\frac{48\sqrt{3}}{27}k + \frac{144\sqrt{3}}{27} \\[0.8em] &= \frac{96\sqrt{3}}{27}k \\[0.8em] &= \frac{32\sqrt{3}}{9}k \end{align*}\]
\[\begin{align*}f'_{k}(x_{2}) &= f'_{k}\left( \textstyle \frac{2\sqrt{3}}{3} \right) \\[0.8em] &= 2k \cdot \left( \frac{2\sqrt{3}}{3} \right)^{3} - 8k \cdot \frac{2\sqrt{3}}{3} \\[0.8em] &= \frac{48\sqrt{3}}{27}k - \frac{16\sqrt{3}}{3}k \\[0.8em] &= \frac{48\sqrt{3}}{27}k - \frac{144\sqrt{3}}{27} \\[0.8em] &= -\frac{96\sqrt{3}}{27}k \\[0.8em] &= -\frac{32\sqrt{3}}{9}k \end{align*}\]
\[\begin{align*}f'_{k}(x_{1}) &= -\frac{1}{f'_{k}(x_{2})} \\[0.8em] f'_{k}\left( \textstyle -\frac{2\sqrt{3}}{3} \right) &= -\frac{1}{f'_{k}\left( \textstyle \frac{2\sqrt{3}}{3} \right)} \\[0.8em] \frac{32\sqrt{3}}{9}k &= -\frac{1}{-\frac{32\sqrt{3}}{9}}k & &| \cdot \frac{32\sqrt{3}}{9}k \\[0.8em] \left( \frac{32\sqrt{3}}{9} \right)^{2} &= 1 \\[0.8em] \frac{1024 \cdot \cancel{3}}{27 \cancel{81}}k^{2} &= 1 & &| \cdot \frac{27}{1024} \\[0.8em] k^{2} &= \frac{27}{1024} & &| \; \sqrt{\quad} \enspace (k > 0) \\[0.8em] k &= \frac{3\sqrt{3}}{32} \\[0.8em] k &\approx 0{,}16 \end{align*}\]
Für \(k = \frac{3\sqrt{3}}{32}\) besitzt der zugehörige Graph der Funktionenschar \(f_{k}\) an den Wendestellen \(x_{1} = -\frac{2\sqrt{3}}{3}\) und \(x_{2} = \frac{2\sqrt{3}}{3}\) zwei zueinander senkrechte Wendetangenten.
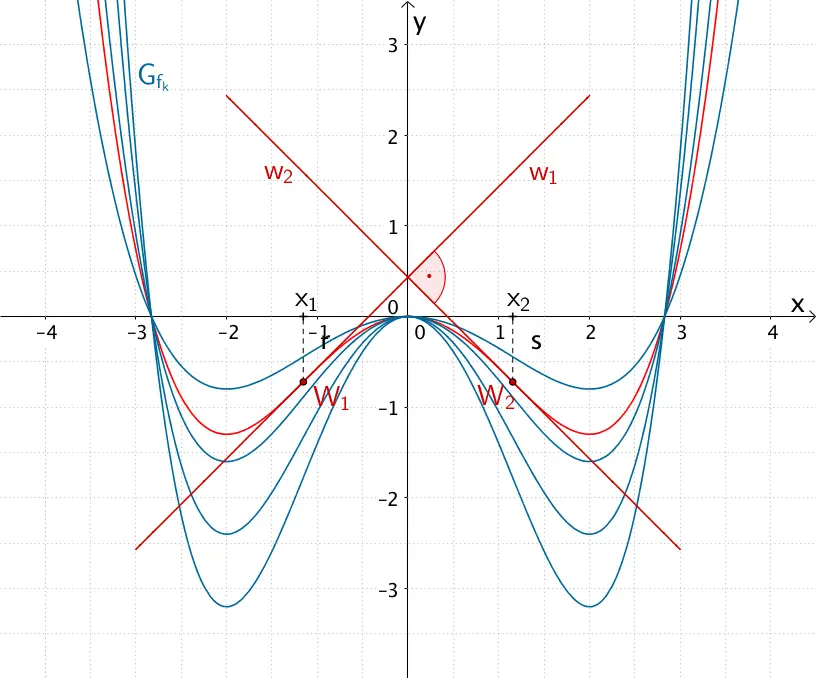
Kurvenschar \(G_{f_{k}}\) der in \(\mathbb R\) definierten Funktionenschar \(f_{k} \colon x \mapsto 0{,}5kx^{4} - 4kx^{2}\) mit \(k > 0\) sowie Graph der Scharfunktion für \(k = \frac{3\sqrt{3}}{32}\) mit den orthogonalen Wendetangenten \(w_{1}\) und \(w_{2}\) an den Wendestellen \(x_{1} = -\frac{2\sqrt{3}}{3}\) und \(x_{2} = \frac{2\sqrt{3}}{3}\)
Besipielaufgabe
Gegeben sei die in \(\mathbb R\) definierte Funktionenschar \(f_{k} \colon x \mapsto 4kx \cdot e^{kx}\) mit \(k > 0\).
a) Bestimmen Sie die Lage und die Art der Extrempunkte der Kurvenschar \(G_{f_{k}}\) der Funktionenschar \(f_{k}\) in Abhängigkeit des Parameters \(k\). Welche besondere Lage haben die Extrempunkte?
b) Ermitteln Sie die Koordinaten der Wendepunkte der Kurvenschar \(G_{f_{k}}\) der Funktionenschar \(f_{k}\) in Abhängigkeit des Parameters \(k\). Welche besondere Lage haben die Wendepunkte?
c) Bestimmen Sie den Wert des Parameters \(k\) so, dass die Wendetangente des zugehörigen Graphen der Funktionenschar \(f_{k}\) parallel zur Winkelhalbierenden des II. und IV. Quadranten verläuft.
\[f_{k}(x) = 4kx \cdot e^{kx}; \; D_{f_{k}} = \mathbb R, \; k > 0\]
a) Extrempunkte der Kurvenschar \(G_{f_{k}}\)
Notwendige Bedingung für Extrempunkte der Kurvenschar \(G_{f_{k}}\) (vgl. Abiturskript - 1.5.3 Monotonieverhalten, Extrem- und Terrassenpunkte):
\[f'_{k}(x) \overset{!}{=} 0\]
Erste Ableitung \(f'_{k}\) bilden:
Der Funktionsterm \(f_{k}(x)\) kann unter Beachtung der Faktorregel und mithilfe der Ableitung der Natürlichen Exponentialfunktion sowie der Produktregel und der Kettenregel abgeleitet werden. Der Parameter \(k\) wird beim Ableiten wie eine Konstante behandelt (vgl. Abiturskript - 1.5.2 Ableitungsregeln).
\[f_{k}(x) = 4kx \cdot e^{kx}\]
\[\begin{align*}f'_{k}(x) &= 4k \cdot 1 \cdot e^{kx} + 4kx \cdot e^{kx} \cdot k \\[0.8em] &= 4ke^{kx} + 4k^{2}e^{kx} \\[0.8em] &= 4ke^{kx} (1 + kx) \end{align*}\]
Nullstellen von \(f'_{k}\) bestimmen:
\[f'_{k}(x) = \underbrace{4ke^{kx}}_{>\, 0} (1 + kx) \enspace (k > 0)\]
Da der Exponentialterm \(4ke^{kx}\) für \(k > 0\) stets größer als Null ist, genügt die Betrachtung der Nullstellen des Faktors \((1 + kx)\) (vgl. Abiturskript - 1.3.1 Eigenschaften und Rechenregeln, Natürliche Exponential- und Logarithmusfunktion).
\[\begin{align*}f'_{k}(x) = 0 \quad \Longrightarrow \quad 1 + kx &= 0 & &| - 1 \\[0.8em] kx &= -1 & &| : k \\[0.8em] x &= -\frac{1}{k} \end{align*}\]
An den Stellen \(x = -\frac{1}{k}\) besitzt die Kurvenschar \(G_{f_{k}}\) waagrechte Tangenten.
Nachweis der Extremstellen:
Die Extremstellen lassen sich mithilfe des Monotoniekriteriums oder mithilfe der zweiten Ableitung \(f''_{k}\) nachweisen (vgl. Abiturskript - 1.5.3 Monotonieverhalten, Extrem- und Terrassenpunkte).
Nachweis der Extremstellen mithilfe des Monotoniekriteriums:
Um den Vorzeichenwechsel von \(f'_{k}\) (Änderung des Monotonieverhaltens) der Kurvenschar \(G_{f_{k}}\) an der Stelle \(x = -\frac{1}{k}\) besser beurteilen zu können, ist es zweckmäßig, den Funktionsterm \(f'_{k}(x)\) entsprechen umzuformen.
\[\begin{align*}f'_{k}(x) &= 4ke^{kx} (1 + kx) \\[0.8em] &= 4ke^{kx} \cdot k \cdot \left(\frac{1}{k} + x \right) \\[0.8em] &= \underbrace{4k^{2}e^{kx}}_{> \, 0} \left( \frac{1}{k} + x \right) & & (k > 0) \end{align*}\]
Der Faktor \(\left( \frac{1}{k} + x \right)\) bestimmt den Vorzeichenwechsel von \(f'_{k}\) an den Stellen \(x = -\frac{1}{k}\).
\[\left. \begin{align*} &f'_{k}\left( \textstyle -\frac{1}{k} \right) = 0 \\[0.8em] &f'_{k}(x) < 0 \; \text{für} \; x < \textstyle -\frac{1}{k} \\[0.8em] &f'_{k}(x) > 0 \; \text{für} \; x > \textstyle -\frac{1}{k} \end{align*} \right\} \enspace \Rightarrow \enspace \text{Tiefpunkte}\; TiP\left( \textstyle -\frac{1}{k} \, \Big| \, f_{k}\left( \textstyle -\frac{1}{k} \right) \right)\]
Veranschaulichung mithilfe einer Monotonietabelle:
| \((k > 0)\) | \(x < -\frac{1}{k}\) | \(x = -\frac{1}{k}\) | \(x > -\frac{1}{k}\) |
| \(4k^{2}e^{kx}\) | \(+\) | \(+\) | \(+\) |
| \(\left( \frac{1}{k} + x \right)\) | \(-\) | \(0\) | \(+\) |
| \(f'_{k}(x)\) | \(-\) | \(0\) | \(+\) |
| \(G_{f_{k}}\) | \(\searrow\) | \(TiP\left( -\frac{1}{k} \, \Big| \, f_{k}\left( -\frac{1}{k} \right) \right)\) | \(\nearrow\) |
Nachweis der Extremstellen mithilfe der zweiten Ableitung \(f''_{k}\):
Die zweite Ableitung \(f''_{k}\) lässt sich unter Beachtung der Faktorregel und mithilfe der Ableitung der Natürlichen Exponentialfunktion sowie der Produktregel und der Kettenregel formulieren. Der Parameter \(k\) wird beim Ableiten wie eine Konstante behandelt (vgl. Abiturskript - 1.5.2 Ableitungsregeln).
\(f'_{k}(x) = 4ke^{kx}(1 + kx)\) (vgl. oben)
\[\begin{align*}f''_{k}(x) &= 4ke^{kx} \cdot k \cdot (1 + k) + 4ke^{kx} \cdot (0 + k) \\[0.8em] &= 4k^{2}e^{kx} (1 + kx) + 4k^{2}e^{kx} \\[0.8em] &= 4k^{2}e^{kx} (1 + kx + 1) \\[0.8em] &= 4k^{2}e^{kx} (2 + kx) \end{align*}\]
Vorzeichen der zweiten Ableitung \(f''_{k}\) an den Extremstellen \(x = -\frac{1}{k}\):
\[\begin{align*} f''_{k}\left( \textstyle -\frac{1}{k} \right) &= 4k^{2}e^{k \cdot \left( -\frac{1}{k} \right)} \left( 2 + k \cdot \left( -\frac{1}{k} \right) \right) \\[0.8em] &= 4k^{2}e^{-1} (2 - 1) & &| \; a^{-n} = \frac{1}{a^{n}} \\[0.8em] &= \frac{4k^{2}}{e} \end{align*}\]
\[\left. \begin{align*} &f'_{k}\left( \textstyle -\frac{1}{k} \right) = 0 \\[0.8em] &f''_{k}\left( \textstyle -\frac{1}{k} \right) > 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Tiefpunkte}\; TiP\left( \textstyle -\frac{1}{k} \, \Big| \, f_{k}\left( \textstyle -\frac{1}{k} \right) \right)\]
Lage (Koordinaten) der Tiefpunkte:
\[x = -\frac{1}{k}\]
\[f_{k}(x) = 4kx \cdot e^{kx}\]
\[\begin{align*} f_{k}\left( \textstyle -\frac{1}{k} \right) &= 4k \cdot \left( -\frac{1}{k} \right) \cdot e^{k \cdot \left( -\frac{1}{k} \right)} \\[0.8em] &= -4e^{-1} & &| \; a^{-n} = \frac{1}{a^{n}} \\[0.8em] &= -\frac{4}{e} \end{align*}\]
\[\Longrightarrow \quad TiP\left( \textstyle -\frac{1}{k} \, \Big| \textstyle -\frac{4}{e} \right)\]
Besondere Lage der Tiefpunkte:
Die \(y\)-Koordinate der Tiefpunkte ist mit \(-\frac{4}{e}\) unabhängig vom Wert des Parameters \(k\) konstant. Folglich liegen alle Tiefpunkte \(TiP \left( -\frac{1}{k} \, \Big| -\frac{4}{e} \right)\) der Kurvenschar \(G_{f_{k}}\) auf einer Geraden mit der Gleichung \(y = -\frac{4}{e}\).
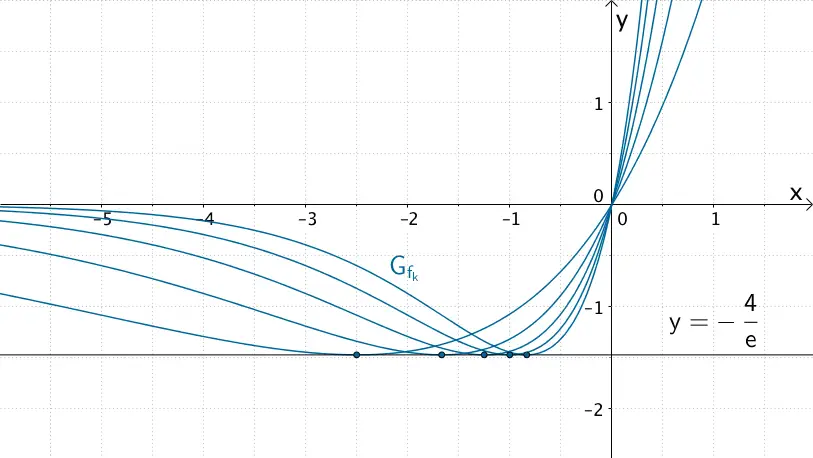
Die Tiefpunkte \(TiP \left( -\frac{1}{k} \, \Big| -\frac{4}{e} \right)\) der Kurvenschar \(G_{f_{k}}\) der in \(\mathbb R\) definierten Funktionenschar \(f_{k} \colon x \mapsto 4kx \cdot e^{kx}\) mit \(k > 0\) liegen auf einer Geraden mit der Gleichung \(y = -\frac{4}{e}\).
b) Wendepunkte der Kurvenschar \(G_{f_{k}}\)
Die Nullstellen von \(f''_{k}\) sind mögliche Wendestellen. Der Nachweis der Wendestellen kann mithilfe des Vorzeichenwechsels von \(f''_{k}\) oder mithilfe der dritten Ableitung \(f'''_{k}\) erfolgen (vgl. Abiturskript - 1.5.4 Krümmungsverhalten und Wendepunkte).
Nullstellen von \(f''_{k}\) bestimmen:
\(f''_{k}(x) = \underbrace{4k^{2}e^{kx}}_{>\,0} (2 + kx)\) (vgl. oben)
Da der Exponentialterm \(4k^{2}e^{kx}\) stets größer als Null ist, genügt die Betrachtung der Nullstellen des Faktors \((2 + kx)\) (vgl. Abiturskript - 1.3.1 Eigenschaften und Rechenregeln, Natürliche Exponential- und Logarithmusfunktion).
\[\begin{align*} f''_{k}(x) = 0 \quad \Longrightarrow \quad 2 + kx &= 0 & &| - 2 \\[0.8em] kx &= -2 & &| : k \\[0.8em] x &= -\frac{2}{k} \end{align*}\]
Die Stellen \(x = -\frac{2}{k}\) sind mögliche Wendestellen der Kurvenschar \(G_{f_{k}}\).
Nachweis der Wendestellen mithilfe von \(f''_{k}\):
Wendestellen \(x = -\frac{2}{k}\) liegen vor, wenn \(f''_{k}\left( -\frac{2}{k} \right) = 0\) gilt, und außerdem \(f''_{k}\) in der Umgebung von \(x = -\frac{2}{k}\) das Vorzeichen wechselt. Um den Vorzeichenwechsel besser beurteilen zu können, wird der Funktionsterm \(f''_{k}(x)\) entsprechend umgeformt.
\[\begin{align*} f''_{k}(x) &= 4k^{2}e^{kx} (2 + kx) \\[0.8em] &= 4k^{2}e^{kx} \cdot k \cdot \left( \frac{2}{k} + x \right) \\[0.8em] &= \underbrace{4k^{3}e^{kx}}_{>\,0}\left( \frac{2}{k} + x \right) & & (k > 0) \end{align*}\]
Der Faktor \(\left( \frac{2}{k} + x \right)\) bestimmt den Vorzeichenwechsel von \(f''_{k}\) an den Stellen \(x = -\frac{2}{k}\).
\[\left. \begin{align*} &f''_{k}\left( \textstyle -\frac{2}{k} \right) = 0 \\[0.8em] &f''_{k}(x) < 0 \; \text{für} \; x < \textstyle -\frac{2}{k} \\[0.8em] &f''_{k}(x) > 0 \; \text{für} \; x > \textstyle -\frac{2}{k} \end{align*} \right\} \enspace \Rightarrow \enspace \text{Wendepunkte}\; W\left( \textstyle -\frac{2}{k} \, \Big| \, f_{k}\left( \textstyle -\frac{2}{k} \right) \right)\]
Veranschaulichung mithilfe einer Krümmungstabelle:
| \(k > 0\) | \(x < -\frac{2}{k}\) | \(x = -\frac{2}{k}\) | \(x > -\frac{2}{k}\) |
| \(4k^{3}e^{kx}\) | \(+\) | \(+\) | \(+\) |
| \(\left(\frac{2}{k} + x \right)\) | \(-\) | \(0\) | \(+\) |
| \(f''_{k}(x)\) | \(-\) | \(0\) | \(+\) |
| \(G_{f_{k}}\) | \(\Large \curvearrowright\) | \(W\left(-\frac{2}{k}\, \Big| \, f_{k}\left( -\frac{2}{k} \right) \right)\) | \(\style{display: inline-block; transform:rotate(0.5turn);}{\Large \curvearrowleft}\) |
Nachweis der Wendestellen mithilfe der dritten Ableitung \(f'''_{k}\):
Wendestellen \(x = -\frac{2}{k}\) liegen vor, wenn \(f''_{k}\left(-\frac{2}{k} \right) = 0\) gilt und zusätzlich die Bedingung \(f'''_{k}\left( -\frac{2}{k} \right) \neq 0\) erfüllt ist.
Dritte Ableitung \(f'''_{k}\) bilden:
Die dritte Ableitung \(f'''_{k}\) kann unter Beachtung der Faktorregel und mithilfe der Ableitung der Natürlichen Exponentialfunktion sowie der Produktregel und der Kettenregel formuliert werden. Der Parameter \(k\) wird beim Ableiten wie eine Konstante behandelt (vgl. Abiturskript - 1.5.2 Ableitungsregeln).
\(f''_{k}(x) = 4k^{2}e^{kx} (2 + kx)\) (vgl. oben)
\[\begin{align*} f'''_{k}(x) &= 4k^{2}e^{kx} \cdot k \cdot (2 + kx) + 4k^{2}e^{kx} \cdot (0 + k) \\[0.8em] &= 4k^{3}e^{kx}(2 + kx) + 4k^{3}e^{kx} \\[0.8em] &= 4k^{3}e^{kx}(2 + kx + 1) \\[0.8em] &= 4k^{3}e^{kx}(3 + kx) \end{align*}\]
\[\begin{align*} f'''_{k}\left( -\frac{2}{k} \right) &= 4k^{3}e^{k \cdot \left( -\frac{2}{k} \right)} \cdot \left( 3 + k \cdot \left( -\frac{2}{k} \right) \right) \\[0.8em] &= 4k^{3}e^{-2} \cdot (3 - 2) & &| \; a^{-n} = \frac{1}{a^{n}} \\[0.8em] &= \underbrace{\frac{4k^{3}}{e^{2}}}_{>\,0} & & (k > 0) \end{align*}\]
\[\left. \begin{align*} &f''_{k}\left( \textstyle -\frac{2}{k} \right) = 0 \\[0.8em] &f'''_{k}\left( -\frac{2}{k} \right) \neq 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Wendepunkte}\; W\left( \textstyle -\frac{2}{k} \, \Big| \, f_{k}\left( \textstyle -\frac{2}{k} \right) \right)\]
Koordinaten der Wendepunkte berechnen:
\[f_{k}(x) = 4kx \cdot e^{kx}\]
\[\begin{align*} f_{k}\left( \textstyle -\frac{2}{k} \right) &= 4k \cdot \left( -\frac{2}{k} \right) \cdot e^{k \cdot \left( -\frac{2}{k} \right)} \\[0.8em] &= -8e^{-2} & &| \; a^{-n} = \frac{1}{a^{n}} \\[0.8em] &= -\frac{8}{e^{2}} \end{align*}\]
\[\Longrightarrow \quad W\left( \textstyle -\frac{2}{k} \, \Big| \textstyle -\frac{8}{e^{2}} \right)\]
Besondere Lage der Wendepunkte:
Die \(y\)-Koordinate der Wendepunkte ist mit \(-\frac{8}{e^{2}}\) unabhängig vom Wert des Parameters \(k\) konstant. Folglich liegen alle Wendepunkte \(W \left( -\frac{2}{k} \, \Big| -\frac{8}{e^{2}} \right)\) der Kurvenschar \(G_{f_{k}}\) auf einer Geraden mit der Gleichung \(y = -\frac{8}{e^{2}}\).
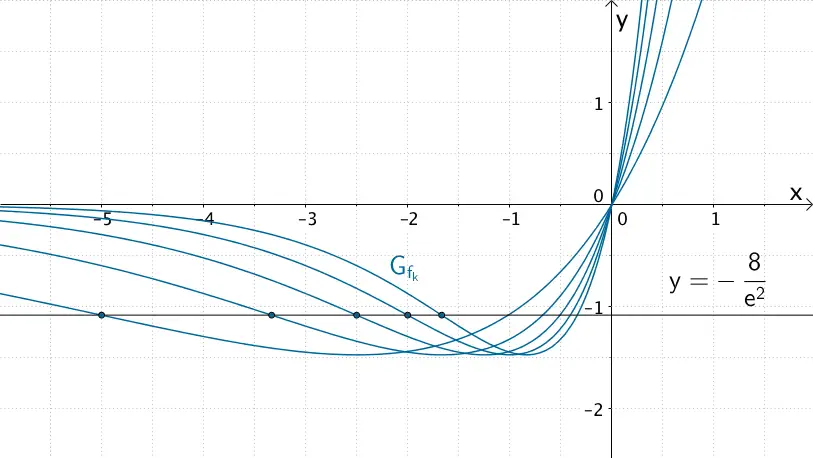
Die Wendepunkte \(W \left( -\frac{2}{k} \, \Big| -\frac{8}{e^{2}} \right)\) der Kurvenschar \(G_{f_{k}}\) der in \(\mathbb R\) definierten Funktionenschar \(f_{k} \colon x \mapsto 4kx \cdot e^{kx}\) mit \(k > 0\) liegen auf einer Geraden mit der Gleichung \(y = -\frac{8}{e^{2}}\).
c) Wert des Parameters \(k\), sodass die Wendetangente parallel zur Winkelhalbierenden des II. und IV. Quadranten verläuft
Mithilfe der Ersten Ableitung \(f'_{k}\) wird zunächst die Steigung \(m_{w}\) der Wendetangenten \(w\) an der Wendestelle \(x = -\frac{2}{k}\) in Abhängigkeit des Parameters \(k\) ermittelt (vgl. Abiturskript - 1.5.1 Die Ableitung, Tangentensteigung).
\(f'_{k}(x) = 4ke^{kx}(1 + kx)\) (vgl. Teilaufgabe a)
Wendestelle: \(x = -\frac{2}{k}\)
\[\begin{align*} m_{w} &= f'_{k}\left( \textstyle -\frac{2}{k} \right) \\[0.8em] &= 4ke^{k \cdot \left( -\frac{2}{k} \right)} \cdot \left( 1 + k \cdot \left( -\frac{2}{k} \right) \right) \\[0.8em] &= 4ke^{-2} \cdot (1 - 2) & &| \; a^{-n} = \frac{1}{a^{n}} \\[0.8em] &= -\frac{4k}{e^{2}} & & (k > 0) \end{align*}\]
Für einen bestimmten Wert des Parameters \(k\) verläuft eine der Wendetangenten \(w\) parallel zur Winkelhalbierenden des II. und IV. Quadranten, wenn deren Steigung gleich der Steigung der Winkelhalbierenden ist (vgl. Abiturskript - 1.1.1 Lineare Funktion, parallele Geraden).
Die Winkelhalbierende des II. und IV. Quadranten mit der Gleichung \(y = -x\) hat die Steigung \(m = -1\).
\[\begin{align*} m_{w} &= -1 \\[0.8em] -\frac{4k}{e^{2}} &= -1 & &| \cdot (-e^{2}) \\[0.8em] 4k &= e^{2} & &| : 4 \\[0.8em] k &= \frac{e^{2}}{4} \\[0.8em] k &\approx 1{,}85 \end{align*}\]
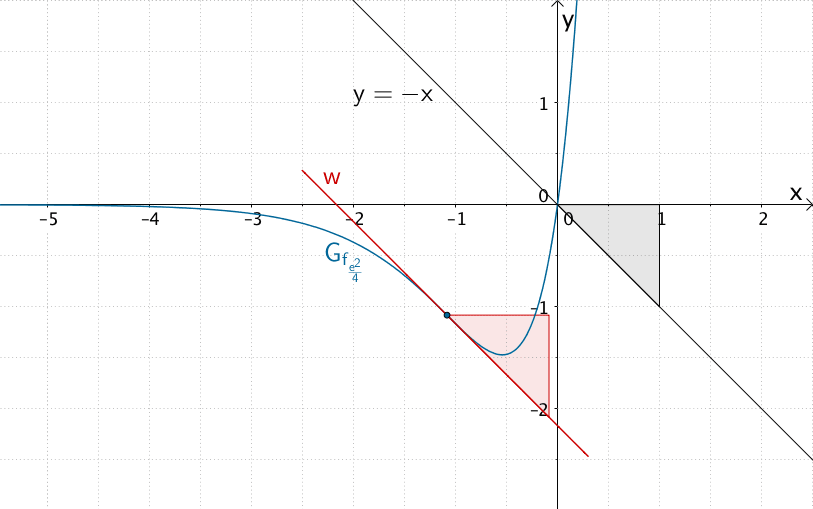
Für \(k = \frac{e^{2}}{4}\) verläuft die Wendetangente \(w\) des zugehörigen Graphen der in \(\mathbb R\) definierten Funktionenschar \(f_{k} \colon x \mapsto 4kx \cdot e^{kx}\) mit \(k > 0\) parallel zur Winkelhalbierenden des II. und IV. Quadranten mit der Gleichung \(y = -x\).


