Ein Integral, dessen Integrationsbereich nach mindestens einer Seite nicht beschränkt ist oder dessen Integrandenfunktion an der unteren oder oberen Integrationsgrenze nicht beschränkt ist, heißt uneigentliches Integral.
1. Der Integrationsbereich ist nach mindestens einer Seite nicht beschränkt
Ist \(f\) eine im Intervall \([a;+\infty[\) bzw. \(]-\infty;b]\) bzw. in \(\mathbb R\) stetige (integrierbare) Funktion, so gilt für \(a, b \in \mathbb R\):
\[\int_{a}^{\infty}f(x)\,dx = \lim \limits_{b \, \to \, \infty} \int_{a}^{b} f(x)\,dx\]
\[\int _{-\infty}^{b} f(x)\,dx = \lim \limits_{a \, \to \, -\infty} \int_{a}^{b} f(x)\, dx\]
\[\int_{-\infty}^{\infty} f(x) \, dx = \int_{-\infty}^{a} f(x)\, dx + \int_{a}^{\infty} f(x)\, dx\]
2. Die Integrandenfunktion ist an einer der Integrationsgrenzen nicht beschränkt
Ist \(f\) eine im Intervall \(]a;b]\) bzw. \([a;b[\) stetige (integrierbare) Funktion mit \(f(x) \to \pm \infty\) für \(x \to a^{+}\) bzw. mit \(f(x) \to \pm \infty\) für \(x \to b^{-}\), so gilt:
\[\int_{a}^{b} f(x)\,dx = \lim \limits_{z \, \to \, a^{+}} \int_{z}^{b} f(x) \, dx\]
bzw.
\[\int_{a}^{b} f(x)\,dx = \lim \limits_{z \, \to \, b^{-}} \int_{a}^{z} f(x) \, dx\]
Ist ein auftretender Grenzwert vorhanden, nennt man das uneigentliche Integral konvergent, andernfalls divergent.
Beispiele:
\[f(x) = \frac{3}{x^{2}}; \; D_{f} = \mathbb R \backslash \{0\}\]
\[\int_{1}^{\infty} \frac{3}{x^{2}} \, dx = \lim \limits_{b \, \to \, \infty} \int_{1}^{b} \frac{3}{x^{2}} \, dx\]
Der Integrationsbereich ist mit \(b \to +\infty\) nicht beschränkt.
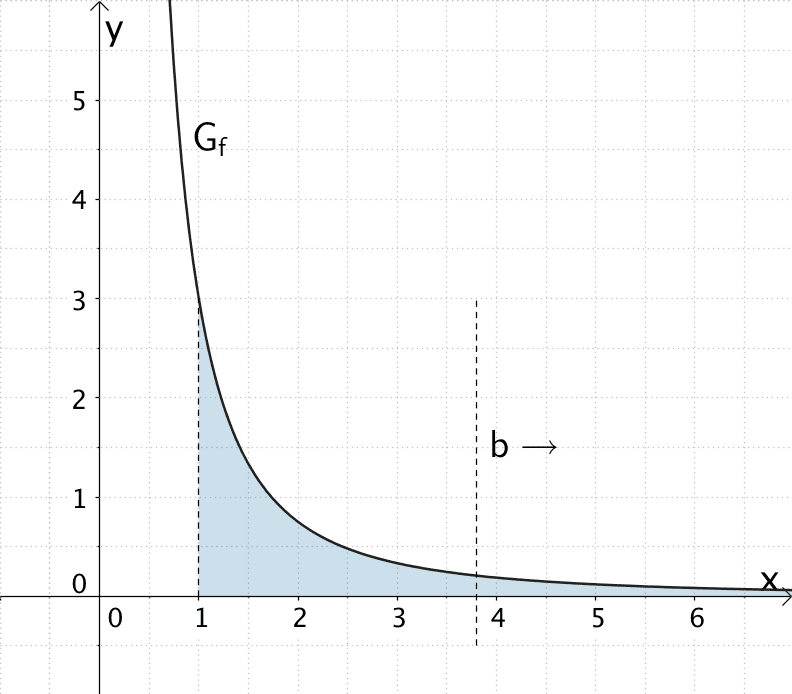
Für \(x \to \infty\) ist die Fläche, welche der Graph der Funktion \(f \colon x \mapsto \dfrac{3}{x^{2}}\) im Intervall \([1;\infty[\) mit der \(x\)-Achse einschließt nach rechts unbegrenzt.
\[f(x) = \frac{3}{x^{2}}; \; D_{f} = \mathbb R \backslash \{0\}\]
\[\int_{0}^{3} \frac{3}{x^{2}} \, dx = \lim \limits_{z \, \to \, 0^{+}} \int_{z}^{3} \frac{3}{x^{2}} \, dx\]
Die Integrandenfunktion \(f \colon x \mapsto \dfrac{3}{x^{2}}\) ist mit \(\lim \limits_{x \, \to \, 0^{+}} \dfrac{3}{x^{2}} = +\infty\) an der Stelle \(x = 0\) nicht beschränkt.
![Für x → 0 ist die Fläche, welche der Graph der Funktion f im Intervall ]0;3] mit der x-Achse einschließt, nach oben unbegrenzt. Für x → 0 ist die Fläche, welche der Graph der Funktion f im Intervall ]0;3] mit der x-Achse einschließt, nach oben unbegrenzt.](/images/stories/abi_check/analysis/Int_Uneigentlich2.png)
Für \(x \to 0^{+}\) ist die Fläche, welche der Graph der Funktion \(f \colon x \mapsto \dfrac{3}{x^{2}}\) im Intervall \(]0;3]\) mit der \(x\)-Achse einschließt nach oben unbegrenzt.
Berechnung uneigentlicher Integrale
Für die Berechnung eines uneigentlichen Integrals wird dieses zunächst in Abhängigkeit der variablen unteren bzw. oberen Integrationsgrenze integralfrei beschrieben. Anschließend erfolgt die entsprechende Grenzwertbetrachtung.
Beispiel:
\[f(x) = \frac{3}{x^{2}}; \; D_{f} = \mathbb R \backslash \{0\}\]
\[\int_{1}^{\infty} \frac{3}{x^{2}} \, dx = \lim \limits_{b \, \to \, \infty} \int_{1}^{b} \frac{3}{x^{2}} \, dx\]
Um das Integral \(\displaystyle \int_{1}^{b} \frac{3}{x^{2}} \, dx\) mit der variablen oberen Integrationsgrenze \(b\) integralfrei beschreiben zu können, wird eine Stammfunktion \(F\) benötigt.
Der Funktionsterm \(F(x)\) der Menge aller Stammfunktionen von \(f\) kann mithilfe des unbestimmten Integrals \(\displaystyle \int x^{r} dx = \frac{x^{r + 1}}{r + 1} + C\) formuliert werden (vgl. Abiturskript - 1.6.2 Unbestimmtes Integral, Wichtige unbestimmte Integrale).
\[f(x) = \frac{3}{x^{2}} = 3x^{-2}\]
\[F(x) = 3 \cdot \frac{1}{-2 + 1}x^{-2 +1} + C = -\frac{3}{x} + C\]
\(\displaystyle \Longrightarrow \quad F_{0}(x) = -\frac{3}{x}\) ist eine Stammfunktion der Funktion \(f\) (für \(C = 0\)).
Integral\(\displaystyle \int_{1}^{b} \frac{3}{x^{2}} \, dx\) integralfrei formulieren:
\[\int_{1}^{b} \frac{3}{x^{2}} \, dx = \left[ -\frac{3}{x} \right]_{1}^{b} = -\frac{3}{b} - \left( -\frac{3}{1} \right) = -\frac{3}{b} + 3\]
Grenzwertbetrachtung durchführen:
\[\int_{1}^{\infty} \frac{3}{x^{2}} \, dx = \lim \limits_{b \, \to \, \infty} \int_{1}^{b} \frac{3}{x^{2}}\, dx = \lim \limits_{b \, \to \, \infty}\, \underbrace{-\frac{3}{b}}_{\to \, 0} + 3 = 3\]
Beispielaufgabe
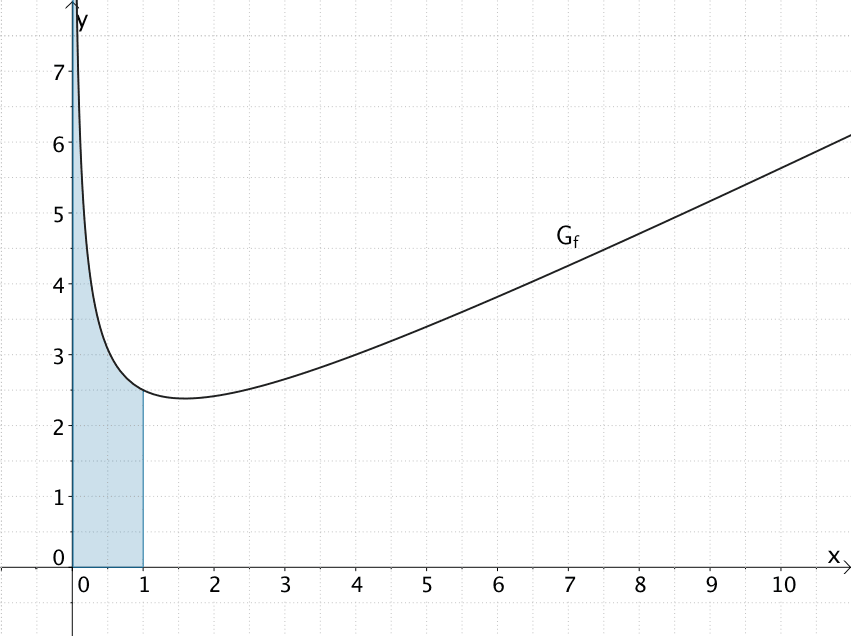
Gegeben sei die in \(\mathbb R^{+}\) definierte Funktion \(f \colon x \mapsto \dfrac{1}{2}x + \dfrac{2}{\sqrt{x}}\).
Weisen Sie nach, dass die Fläche, welche \(G_{f}\) mit den Koordinatenachsen und der Geraden \(x = 1\) einschließt (vgl. Abbildung) einen endlichen Flächeninhalt hat und geben sie diesen an.
Der Graph der Funktion \(f\), die Gerade \(y = \dfrac{1}{2}x\) sowie die beiden Geraden \(x = 1\) und \(x = b\) begrenzen mit \(b > 1\) eine Fläche mit dem Flächeninhalt \(A(b)\). Bestimmen Sie den Flächeninhalt \(A(b)\) für \(b \to \infty\) und deuten Sie das Ergebnis geometrisch.
Nachweis, dass die Fläche, welche \(G_{f}\) mit den Koordinatenachsen und der Geraden \(x = 1\) einschließt, einen endlichen Flächeninhalt hat
\[f(x) = \frac{1}{2}x + \frac{2}{\sqrt{x}}\,; \enspace D_{f} = \mathbb R^{+}\]
Der Flächeninhalt \(A\), der für \(x \to 0\) nach oben unbegrenzten Fläche lässt sich als uneigentliches Integral beschreiben.
\[A = \int_{0}^{1} f(x) \, dx = \lim \limits_{z \, \to \, 0^{+}} \int_{z}^{1} \left( \frac{1}{2}x + \frac{2}{\sqrt{x}} \right) dx\]
Integral \(\displaystyle \int_{z}^{1} \left( \frac{1}{2}x + \frac{2}{\sqrt{x}} \right) dx\) integralfrei formulieren:
Hierfür wird eine Stammfunktion der Funktion \(f\) benötigt. Der Funktionsterm \(F(x)\) der Menge aller Stammfunktionen von \(f\) kann mithilfe des unbestimmten Integrals \(\displaystyle \int x^{r} dx = \frac{x^{r + 1}}{r + 1} + C\) formuliert werden (vgl. Abiturskript - 1.6.2 Unbestimmtes Integral, Wichtige unbestimmte Integrale).
\[f(x) = \frac{1}{2}x + \frac{2}{\sqrt{x}} = \frac{1}{2}x + 2 \cdot x^{-\frac{1}{2}}\]
\[\begin{align*} F(x) &= \frac{1}{2} \cdot \frac{1}{1 + 1}x^{1 + 1} + 2 \cdot \frac{1}{-\frac{1}{2} + 1}x^{-\frac{1}{2} + 1} + C \\[0.8em] &= \frac{1}{4}x^{2} + 4x^{\frac{1}{2}} + C \\[0.8em] &= \frac{1}{4}x^{2} + 4\sqrt{x} + C \end{align*}\]
\(\displaystyle \Longrightarrow \quad F_{0}(x) = \frac{1}{4}x^{2} + 4\sqrt{x}\) ist eine Stammfunktion der Funktion \(f\) (für \(C = 0\)).
\[\begin{align*} \int_{z}^{1} \left( \frac{1}{2}x + \frac{2}{\sqrt{x}} \right) dx &= \left[ \frac{1}{4}x^{2} + 4\sqrt{x} \right]_{z}^{1} \\[0.8em] &= \frac{1}{4} \cdot 1^{2} + 4\sqrt{1} - \left( \frac{1}{4}z^{2} + 4\sqrt{z} \right) \\[0.8em] &= 4{,}25 - \frac{1}{4}z^{2} - 4\sqrt{z} \end{align*}\]
Grenzwertbetrachtung \(z \to 0^{+}\) durchführen:
\[A = \lim \limits_{z \, \to \, 0^{+}} \int_{z}^{1} \left( \frac{1}{2}x + \frac{2}{\sqrt{x}} \right) dx = \lim \limits_{z \, \to \, 0^{+}} 4{,}25 - \underbrace{\frac{1}{4}z^{2} - 4\sqrt{z}}_{\to \, 0} = 4{,}25\]
Schlussfolgerung:
Die Fläche, welche \(G_{f}\) mit den Koordinatenachsen und der Geraden \(x = 1\) einschließt, hat den endlichen Flächeninhalt 4,25 FE (Flächeneinheiten).
Flächeninhalt \(A(b)\) für \(b \to \infty\)
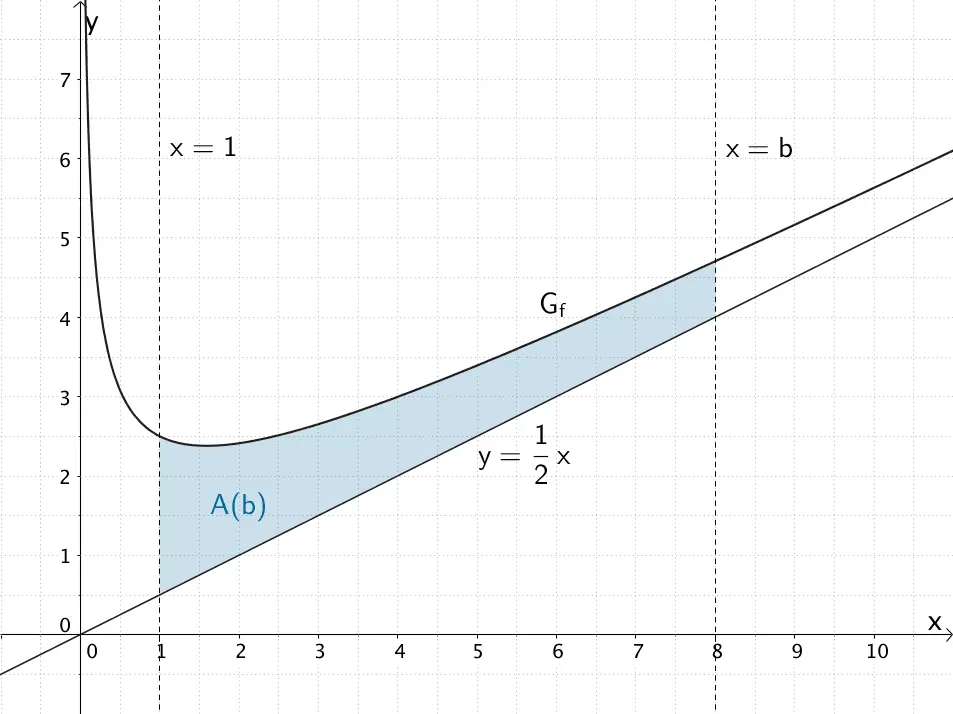
Flächeninhalt \(A(b)\) der Fläche, welche der Graph der Funktion \(f\), die Gerade \(y = \dfrac{1}{2}x\) sowie die beiden Geraden \(x = 1\) und \(x = b\) (\(b > 1\)) begrenzen.
Der Flächeninhalt \(A(b)\), der für \(b \to \infty\) nach rechts unbegrenzten Fläche lässt sich als uneigentliches Integral beschreiben (vgl. Abiturskript - 1.6.4 Flächenberechnung, Flächeninhalt zwischen zwei Funktionsgraphen).
\[f(x) = \frac{1}{2}x + \frac{2}{\sqrt{x}}\]
\[\begin{align*}A(b) &= \lim \limits_{b \, \to \, \infty} \int_{1}^{b} \left( f(x) - \frac{1}{2}x \right) dx \\[0.8em] &= \lim \limits_{b \, \to \, \infty} \int_{1}^{b} \left( \frac{1}{2}x + \frac{2}{\sqrt{x}} - \frac{1}{2}x \right) dx \\[0.8em] &= \lim \limits_{b \, \to \, \infty} \int_{1}^{b} \frac{2}{\sqrt{x}}\, dx \end{align*}\]
Integral \(\displaystyle \int_{1}^{b} \frac{2}{\sqrt{x}} \, dx\) integralfrei formulieren:
Hierfür wird eine Stammfunktion der Integrandenfunktion \(\displaystyle x \mapsto \frac{2}{\sqrt{x}}\) benötigt. Der Funktionsterm der Menge aller Stammfunktionen der Integrandenfunktion \(\displaystyle x \mapsto \frac{2}{\sqrt{x}}\) kann mithilfe des unbestimmten Integrals \(\displaystyle \int x^{r} dx = \frac{x^{r + 1}}{r + 1} + C\) formuliert werden (vgl. Abiturskript - 1.6.2 Unbestimmtes Integral, Wichtige unbestimmte Integrale).
\[\frac{2}{\sqrt{x}} = 2 x^{-\frac{1}{2}}\]
\[\int 2 x^{-\frac{1}{2}} \, dx = 2 \cdot \frac{1}{-\frac{1}{2} + 1} \cdot x^{-\frac{1}{2} + 1} + C = 4x^{\frac{1}{2}} + C = 4\sqrt{x} + C\]
\(\Longrightarrow \quad\) Die Funktion \(x \mapsto 4\sqrt{x}\) ist eine Stammfunktion der Integrandenfunktion \(x \mapsto \dfrac{2}{\sqrt{x}}\) (für \(C = 0\)).
\[\int_{1}^{b} \frac{2}{\sqrt{x}} \, dx = \left[ 4\sqrt{x} \right]_{1}^{b} = 4\sqrt{b} - 4\sqrt{1} = 4(\sqrt{b} - 1)\]
Grenzwertbetrachtung \(b \to \infty\) durchführen:
\[A(b) = \lim \limits_{b \, \to \, \infty} \int_{1}^{b} \frac{2}{\sqrt{x}} \, dx = \lim \limits_{b \, \to \, \infty} 4(\underbrace{\sqrt{b} - 1}_{\to \, \infty}) = \infty\]
Geometrische Bedeutung des Ergebnisses:
Die Fläche, welche der Graph der Funktion \(f \colon x \mapsto \dfrac{1}{2}x + \dfrac{2}{\sqrt{x}}\), die Gerade \(y = \dfrac{1}{2}x\) sowie die Geraden \(x = 1\) und \(x = b\) (b > 1) für \(b \to \infty\) begrenzen, hat keinen endlichen Flächeninhalt.


