Ableitung einer Potenzfunktion

Bestimmen Sie den Term der Ableitungsfunktion \(f'\) von \(f\) und geben Sie die maximale Definitionsmenge von \(f'\) an.

Bestimmen Sie  \(\lim \limits_{x \, \to \, 6} f'(x)\) und beschreiben Sie, welche Eigenschaft von \(G_f\) aus diesem Ergebnis folgt.

(zur Kontrolle: \(\displaystyle f'(x) = \frac{1}{\sqrt{12 - 2x}}\))

(5 BE)

Gegeben ist die Funktion \(\displaystyle h \colon x \mapsto \frac{3}{e^{x + 1} - 1}\) mit Definitionsbereich \(D_{h} = ]-1;+\infty[\). Abbildung 2 zeigt den Graphen \(G_{h}\) von \(h\).

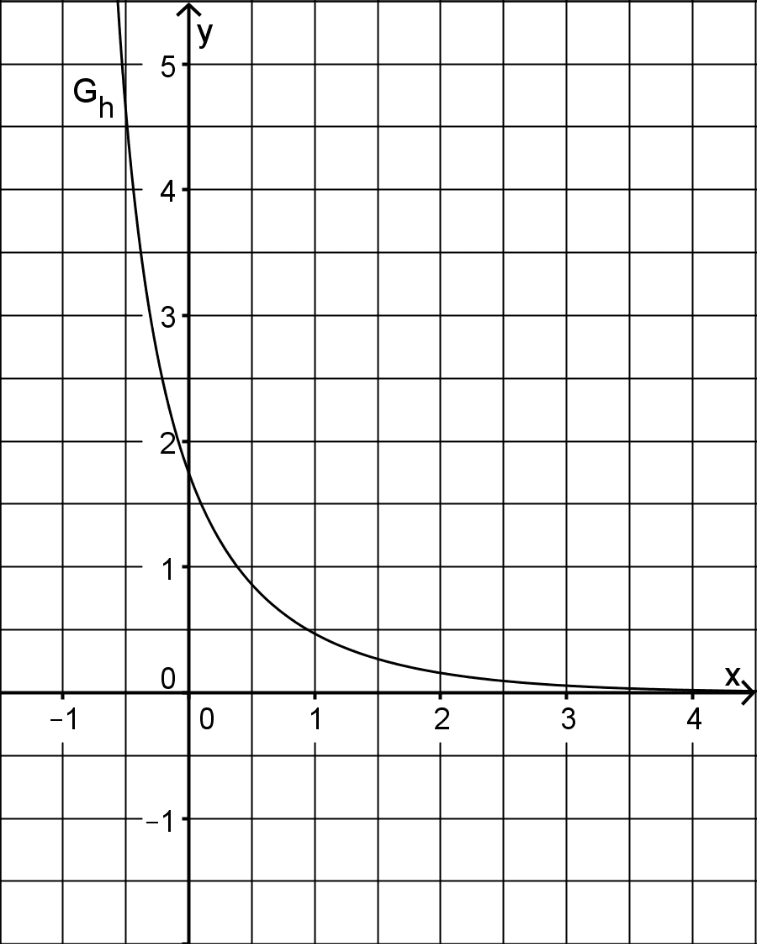Abb. 2

Begründen Sie anhand des Funktionsterms, das \(\lim \limits_{x \, \to \, +\infty} h(x) = 0\) gilt.

Zeigen Sie rechnerisch für \(x \in D_{h}\), dass für die Ableitung \(h'\) von \(h\) gilt: \(h'(x) < 0\).

(4 BE)

Bestimmen Sie Lage und Art des Extrempunkts von \(G_{f}\).

(4 BE)

Es gibt Punkte des Querschnitts der Tunnelwand, deren Abstand zu \(M\) minimal ist. Bestimmen Sie die \(x\)-Koordinaten der Punkte \(P_{x}\), für die \(d(x)\) minimal ist, und geben Sie davon ausgehend diesen minimalen Abstand an.

(5 BE)

Ermitteln Sie den Zeitpunkt nach Beginn der Messung, zu dem die momentane Änderungsrate der Anzahl der Pollen in einem Kubikmeter Luft \(-30\frac{\textsf{1}}{\textsf{h}}\) beträgt.

(2 BE)

Überprüfen Sie rechnerisch, ob das Fenster bei seiner Drehung am Möbelstück anstoßen kann.

(5 BE)

Zeigen Sie, dass dieser Abstand mit der minimalen Entfernung des Hubschraubers vom Mittelpunkt des Grundstücks übereinstimmt, der im Modell durch den Punkt \(M(-40|30|30)\) dargestellt wird.

(5 BE)

Geben Sie den Term einer in \(\mathbb R\) definierten Funktion \(f\) an, sodass die in \(\mathbb R\) definierte Integralfunktion \(\displaystyle F \colon x \mapsto \int_{-1}^x f(t)\,dt\) genau zwei Nullstellen besitzt. Geben Sie die Nullstellen von \(F\) an.

(3 BE)

Im Modell gibt es einen Zeitpunkt \(x_M\), zu dem die Blumen am schnellsten wachsen. Bestimmen Sie mithilfe von Abbildung 2 einen Näherungswert für \(x_M\). Ermitteln Sie anschließend einen Näherungswert für die maximale Wachstumsrate in Zentimetern pro Tag.

(5 BE)

Ein den oberen Rand des Kunstwerks genauer darstellendes Modell liefert der Graph der in \(\mathbb R\) definierten ganzrationalen Funktion \(q\) vierten Grades mit \(q(x) = -0{,}11x^4 - 0{,}81x^2 + 5\,\). Der Graph von \(q\) wird mit \(G_q\) bezeichnet.

Weisen Sie rechnerisch nach, dass \(G_q\) symmetrisch bezüglich der \(y\)-Achse ist, durch die Punkte \(A\) und \(B\) verläuft und genau einen Extrempunkt besitzt.

(7 BE)

Im Intervall \(]0;2[\) gibt es eine Stelle \(x_0\), an der der Wert der Differenz \(d(x) = q(x) - p(x)\) maximal wird. Berechnen Sie \(x_0\) sowie den Wert der zugehörigen Differenz.

(5 BE)

Geben Sie das Verhalten von \(g\) für \(x \to -\infty\) und \(x \to +\infty\) an.

(2 BE)

Geben Sie zu den Funktionstermen jeweils den maximalen Definitionsbereich sowie einen Term der Ableitungsfunktion an.

\[g(x)= \frac{3}{x^2 - 1}\]

(3 BE)

Zeigen Sie, dass \(F : x \mapsto \frac{1}{4}x^2 \cdot (2\ln x - 1)\) mit Definitionsmenge \(\mathbb R^+\) eine Stammfunktion der in \(\mathbb R^+\) definierten Funktion \(f : x \mapsto x \cdot \ln x\) ist. Bestimmen Sie den Term derjenigen Stammfunktion von \(f\), die in \(x = 1\) eine Nullstelle hat.

(5 BE)

Bestimmen Sie rechnerisch die Koordinaten desjenigen Graphenpunkts \(Q_E(x_E|y_E)\), der von \(P\) den kleinsten Abstand hat. Tragen Sie \(Q_E\) in Abbildung 1 ein.

(zur Kontrolle: \(x_E = 1\))

(7 BE)

Weisen Sie nach, dass die Verbindungsstrecke \([PQ_E]\) und die Tangente an \(G_f\) im Punkt \(Q_E\) senkrecht zueinander sind.

(5 BE)

Bestimmen Sie den Term der Ableitung von \(f\).

(2 BE)

Bestimmen Sie rechnerisch Lage und Art der Extrempunkte von \(G_f\).

(zur Kontrolle: \(f'(x) = 2e^{-0{,}5x^2} \cdot (1 - x^2)\,\); y-Koordinate des Hochpunkts: \(\frac{2}{\sqrt{e}}\))

(6 BE)

Bestimmen Sie einen Näherungswert \(x_1\) für die \(x\)-Koordinate dieses Schnittpunkts, indem Sie für die in \(\mathbb R\) definierte Funktion \(d \colon x \mapsto g(x) - h(x)\) den ersten Schritt des Newton-Verfahrens mit dem Startwert \(x_0 = 1\) durchführen.

(4 BE)

Bestimmen Sie rechnerisch Lage und Art der Extrempunkte von \(G_f\,\).

(8 BE)