Abstand zwischen Punkt und Ebene

Berechnen Sie die Größe des Neigungswinkels der Seitenkante \([BS]\) gegen die Ebene \(E\) sowie das Volumen \(V\) der Pyramide.

(Teilergebnis: \(V = 216\))

(7 BE)

Welche Lagebeziehung muss eine Gerade zur Ebene \(E\) haben, wenn für jeden Punkt \(P\) dieser Geraden die Pyramide \(ABCP\) das gleiche Volumen wie die Pyramide \(ABCS\) besitzen soll? Begründen Sie Ihre Antwort.

(3 BE)

Das Prisma ist das Modell eines Holzkörpers, der auf einer durch die \(x_1x_2\)-Ebene beschriebenen horizontalen Fläche liegt. Der Punkt \(M\,(5|6{,}5|3)\) ist Mittelpunkt einer Kugel, die die Seitenfläche \(BSTC\) im Punkt \(W\) berührt.

Berechnen Sie den Radius \(r\) der Kugel sowie die Koordinaten von \(W\,\).

(Teilergebnis: \(r = 1{,}5\))

(6 BE)

Abbildung 2 zeigt ein quaderförmiges Möbelstück, das 40 cm hoch ist. Es steht mit seiner Rückseite flächenbündig an der Wand unter dem Fenster. Seine vordere Oberkante liegt im Modell auf der Geraden \(k \colon \enspace \overrightarrow X = \begin{pmatrix} 0 \\ 5{,}5 \\ 0{,}4 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}\), \(\lambda \in \mathbb R\,\).

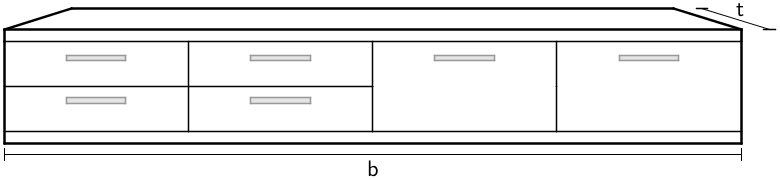Abb. 2

Ermitteln Sie mithilfe von Abbildung 2 die Breite \(b\) des Möbelstücks möglichst genau.

Bestimmen Sie mithilfe der Gleichung der Geraden \(k\) die Tiefe \(t\) des Möbelstücks und erläutern Sie Ihr Vorgehen.

(4 BE)

Ein Hubschrauber überfliegt das Grundstück entlang einer Linie, die im Modell durch die Gerade

\[g\colon \enspace \overrightarrow X = \begin {pmatrix} -20 \\ 40 \\ 40 \end {pmatrix} + \lambda \cdot \begin {pmatrix} 4 \\ 5 \\ -3 \end {pmatrix}\,, \enspace \lambda \in \mathbb R \;,\]

beschrieben wird.

Weisen Sie nach, dass der Hubschrauber mit einem konstanten Abstand von 20 m zum Hang fliegt.

(3 BE)

Berechnen Sie den Abstand des Punktes \(R\) von der Ebene \(E\).

(2 BE)

Der Innenausbau des Pavillons erfordert eine möglichst kurze, dünne Strebe zwischen dem Mittelpunkt der Grundfläche und der südlichen Außenwand. Ermitteln Sie, in welcher Höhe über der Grundfläche die Strebe an der Außenwand befestigt ist.

(5 BE)