Analysis 1

Geben ist die Funktion \(f \colon x \mapsto 2 - \ln{(x - 1)}\) mit maximalem Definitionsbereich \(D_{f}\). Der Graph von \(f\) wird mit \(G_{f}\) bezeichnet.

Zeigen Sie, dass \(D_{f} = \; ]1;+\infty[\) ist, und geben Sie das Verhalten von \(f\) an den Grenzen des Definitionsbereichs an.

(3 BE)

Berechnen Sie die Nullstelle von \(f\).

(2 BE)

Beschreiben Sie, wie \(G_{f}\) schrittweise aus dem Graphen der in \(\mathbb R^{+}\) definierten Funktion \(x \mapsto \ln{x}\) hervorgeht. Erklären Sie damit das Monotonieverhalten von \(G_{f}\).

(5 BE)

Zeigen Sie, dass \(F \colon x \mapsto 3x - (x - 1) \cdot \ln{(x - 1)}\) mit Definitionsbereich \(D_{f} = \; ]1; +\infty[\) eine Stammfunktion von \(f\) ist, und bestimmen Sie den Term der Stammfunktion von \(f\), die bei \(x = 2\) eine Nullstelle hat.

(4 BE)

Berechnen Sie den Wert des Integrals \(\displaystyle \int_1^2 f(x)dx\).

(3 BE)

Betrachtet werden für \(k \in \mathbb R\) die in \(]-\infty;0]\) definierten Funktionen \(f_k \colon x \mapsto f(x) + k\). Somit gilt \(f_0(x) = f(x)\), wobei sich \(f_0\) und \(f\) im Definitionsbereich unterscheiden.

Begründen Sie mithilfe der ersten Ableitung von \(\boldsymbol{f_k}\), dass \(f_k\) für jeden Wert von \(k\) umkehrbar ist. Skizzieren Sie in Abbildung 1 den Graphen der Umkehrfunktion von \(f_0\).

(4 BE) 

Der Graph von \(f\) schließt mit der \(x\)-Achse sowie den Geraden mit den Gleichungen \(x = 1\) und \(x = b\) mit \(b > 1\) ein Flächenstück ein. Bestimmen Sie denjenigen Wert von \(b\), für den dieses Flächenstück den Inhalt 1 hat.

(3 BE)

Berechnen Sie auf der Grundlage des Modells die Größe des Winkels \(\alpha\), den das Plateau und die Fahrbahn an der Kante zur Abfahrt einschließen (vgl. Abbildung 2).

(2 BE)

Die vordere Seitenfläche des Hinderniselements wird in Teilbereichen der Auf- und Abfahrt als Werbefläche verwendet (vgl. Abbildung 1). Im Modell handelt es sich um zwei Flächenstücke, nämlich um die Fläche zwischen \(G_{f}\) und der \(x\)-Achse im Bereich \(2 \leq x \leq 6\) sowie die dazu symmetrische Fläche im II-Quadranten. Berechnen Sie unter Verwendung der in Aufgabe 1d angegebenen Stammfunktion \(F\), wie viele Quadratmeter als Werbefläche zur Verfügung stehen.

(3 BE)

Betrachtet wird die Schar der in \(\mathbb R\) definierten Funktionen \(g_{k} \colon x \mapsto kx^{3} + 3 \cdot (k + 1)x^{2} + 9x\) mit \(k \in \mathbb R \backslash \{0\}\) und den zugehörigen Graphen \(G_{k}\). Für jedes \(k\) besitzt der Graph \(G_{k}\) genau einen Wendepunkt \(W_{k}\).

Geben Sie das Verhalten von \(g_{k}\) an den Grenzen des Definitionsbereichs in Abhängigkeit von \(k\) an.

(2 BE)

Bestimmen Sie die \(x\)-Koordinate von \(W_{k}\) in Abhängigkeit von \(k\).

(zur Kontrolle: \(x = -\frac{1}{k} - 1\))

(3 BE)

Bestimmen Sie den Wert von \(k\) so, dass der zugehörige Wendepunkt \(W_{k}\) auf der \(y\)-Achse liegt. Zeigen Sie, dass in diesem Fall der Punkt \(W_{k}\) im Koordinatenursprung liegt und die Wendetangente, d. h. die Tangente an \(G_{k}\) im Punkt \(W_{k}\), die Steigung \(9\) hat.

(4 BE)

Gegeben ist die in \(\mathbb R \backslash \{0\}\) definierte Funktion \(f \colon x \mapsto \dfrac{1}{x^2}+1\).

Geben Sie eine Gleichung der senkrechten und eine Gleichung der waagrechten Asymptote des Graphen von \(f\) an.

(2 BE)

Der Graph \(G_f\) besitzt in genau einem Punkt eine waagrechte Tangente. Bestimmen Sie die Koordinaten dieses Punkts und begründen Sie, dass es sich um einen Hochpunkt handelt.

(zur Kontrolle: \(f'(x) = \dfrac{10 - 2x}{\sqrt{10x - x^2}}\); \(y\)-Koordinate des Hochpunkts: \(10\))

(5 BE)

Betrachtet wird die in \(\mathbb R^{+}\) definierte Funktion \(f\) mit \(f(x) = \dfrac{1}{\sqrt{x^{3}}}\).

Zeigen Sie, dass die in \(\mathbb R^{+}\) definierte Funktion \(F\) mit \(F(x) = -\dfrac{2}{\sqrt{x}}\) eine Stammfunktion von \(f\) ist.

(2 BE)

Die Abbildung 1 zeigt den Graphen \(G_{f'}\) der Ableitungsfunktion \(f'\) einer in \(\mathbb R\) definierten ganzrationalen Funktion \(f\). Nur in den Punkten \((-4|f'(-4))\) und \((5|f'(5))\) hat der Graph \(G_{f'}\) waagrechte Tangenten.

Begründen Sie, dass \(f\) genau eine Wendestelle besitzt. 

(2 BE)

Es gibt Tangenten an den Graphen von \(f\), die parallel zur Winkelhalbierenden des I. und III. Quadranten sind. Ermitteln Sie anhand des Graphen \(\mathbf{G_{f'}}\) der Ableitungsfunktion \(f'\) in der Abbildung 1 Näherungswerte für die \(x\)-Koordinaten derjenigen Punkte, in denen der Graph von \(f\) jeweils eine solche Tangente hat.

(2 BE)

Gegeben sind die in \(\mathbb R\) definierten Funktionen \(f \colon x \mapsto x^{2} + 4\) und \(g_{m} \colon x \mapsto m \cdot x\) mit \(m \in \mathbb R\). Der Graph von \(f\) wird mit \(G_{f}\) und der Graph von \(g_{m}\) mit \(G_{m}\) bezeichnet.

Skizzieren Sie \(G_{f}\) in einem Koordinatensystem. Berechnen Sie die Koordinaten des gemeinsamen Punkts der Graphen \(G_{f}\) und \(G_{4}\).

(3 BE)

Es gibt Werte von \(m\), für die die Graphen \(G_{f}\) und \(G_{m}\) jeweils keinen gemeinsamen Punkt haben. Geben Sie diese Werte von \(m\) an.

(2 BE)

Gegeben ist die Funktion \(g\) mit \(g(x) = 0{,}7 \cdot e^{0{,}5x} - 0{,}7\) und \(x \in \mathbb R\). Die Funktion \(g\) ist umkehrbar. Die Abbildung 2 zeigt den Graphen \(G_{g}\) von \(g\) sowie einen Teil des Graphen \(G_{h}\) der Umkehrfunktion \(h\) von \(g\).

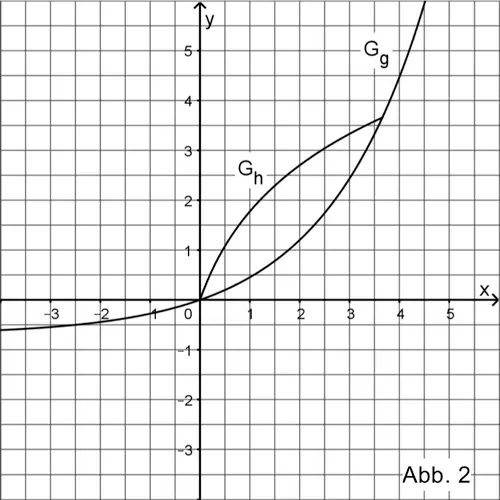
Zeichnen Sie in die Abbildung 2 den darin fehlenden Teil von \(G_{h}\) ein.

(2 BE)