Die Abbildung zeigt den Graphen der Dichtefunktion der normalverteilten Zufallsgröße \(A\).
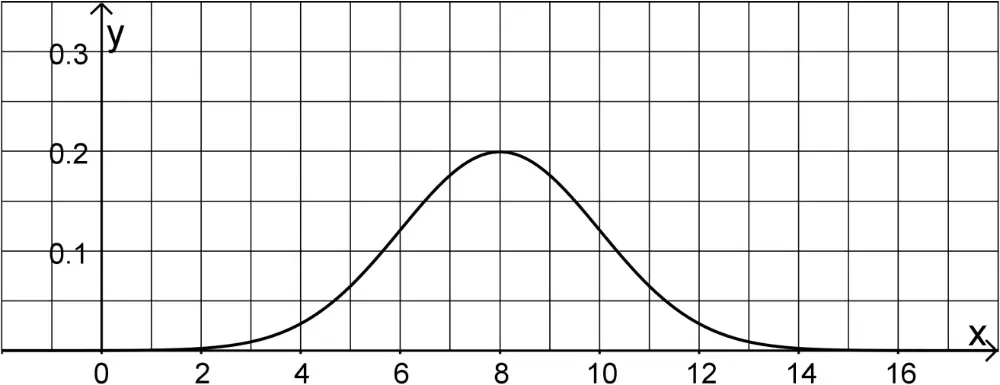
- Die Wahrscheinlichkeit dafür, dass \(A\) einen Wert aus dem Intervall \([6;10]\) annimmt, beträgt etwa 68 %. Berechnen Sie die Wahrscheinlichkeit dafür, dass \(A\) einen Wert annimmt, der größer als 10 ist.
(2 BE)
- Die Zufallsgröße \(B\) ist ebenfalls normalverteilt; der Erwartungswert von \(B\) ist ebenso groß wie der Erwartungswert von \(A\), die Standardabweichung von \(B\) ist größer als die Standarabweichung von \(A\). Skizzieren Sie in der Abbildung einen möglichen Graphen der Dichtefunktion von \(B\).
(3 BE)