- Details
- Kategorie: Analysis 1
Gegeben ist die in \(\mathbb R \backslash \{0\}\) definierte Funktion \(f \colon x \mapsto \dfrac{1}{x^2}+1\).
Geben Sie eine Gleichung der senkrechten und eine Gleichung der waagrechten Asymptote des Graphen von \(f\) an.
(2 BE)
- Details
- Kategorie: Analysis 1
Berechnen Sie den Wert des Integrals \(\displaystyle \int_1^2 f(x)dx\).
(3 BE)
- Details
- Kategorie: Analysis 1
Gegeben ist die in \(\mathbb R\) definierte Funktion \(g \colon x \mapsto x^2-e^x\). Der Graph von \(g\) besitzt genau einen Wendepunkt \(W\). Bestimmen Sie rechnerisch die \(x\)-Koordinate von \(W\) und beurteilen Sie, ob \(W\) oberhalb der \(x\)-Achse liegt.
(5 BE)
- Details
- Kategorie: Analysis 1
Abbildung 1 zeigt den Graphen der in \(\mathbb R\) definierten Funktion \(f\) mit \(f(x) = 3 \cdot \cos{(x)}\).
Geben Sie den Wert des Integrals \(\displaystyle \int_0^{\pi} f(x)dx\) an.
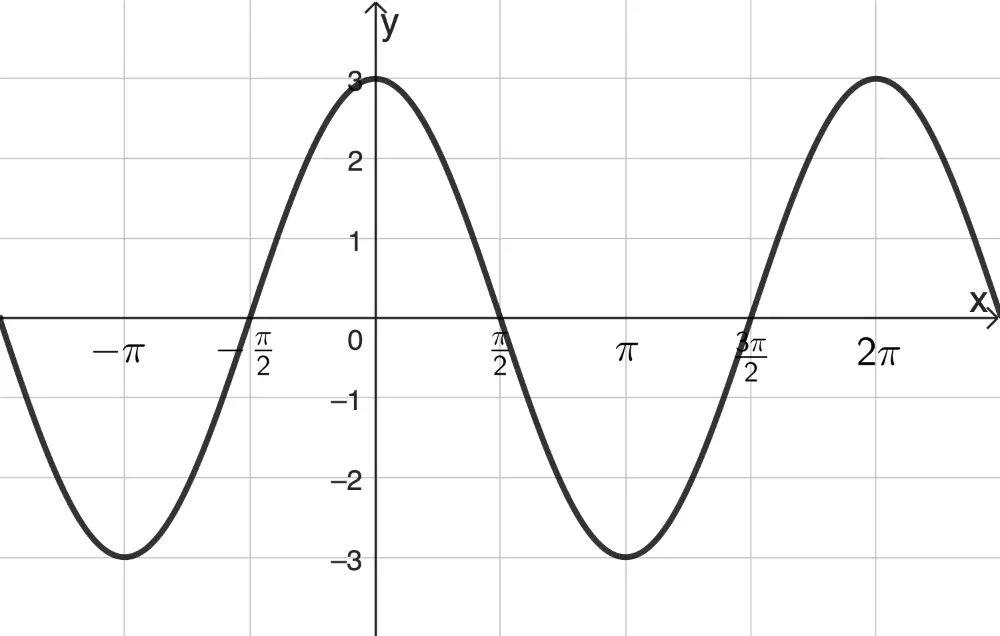Abb. 1
(1 BE)
- Details
- Kategorie: Analysis 1
Die in \(\mathbb R\) definierte Funktion \(g\) ist gegeben durch \(g(x) = a \cdot f(x) + b \cdot x\) mit reellen Zahlen \(a\) und \(b\). Die Punkte \((0|-3)\) und \(\big(\frac{\pi}{2}| \frac{3}{4}\pi \big)\) liegen auf dem Graphen von \(g\). Ermitteln Sie \(a\) und \(b\).
(4 BE)
- Details
- Kategorie: Analysis 1
Gegeben sind die in \(\mathbb R_0^+\) definierten Funktionen \(f\) und \(g\), wobei \(g\) die Umkehrfunktion von \(f\) ist. Abbildung 2 zeigt die Graphen \(G_f\) von \(f\) und \(G_g\) von \(g\). \(G_f\) und \(G_g\) schneiden sich nur im Koordinatenursprung und im Punkt \((x_S|f(x_S))\).
Beurteilen Sie folgende Aussage:
\[\int_0^{x_S}\left( g(x) - f(x) \right)dx = 2 \cdot \int_0^{x_S}\left( x - f(x) \right)dx\]
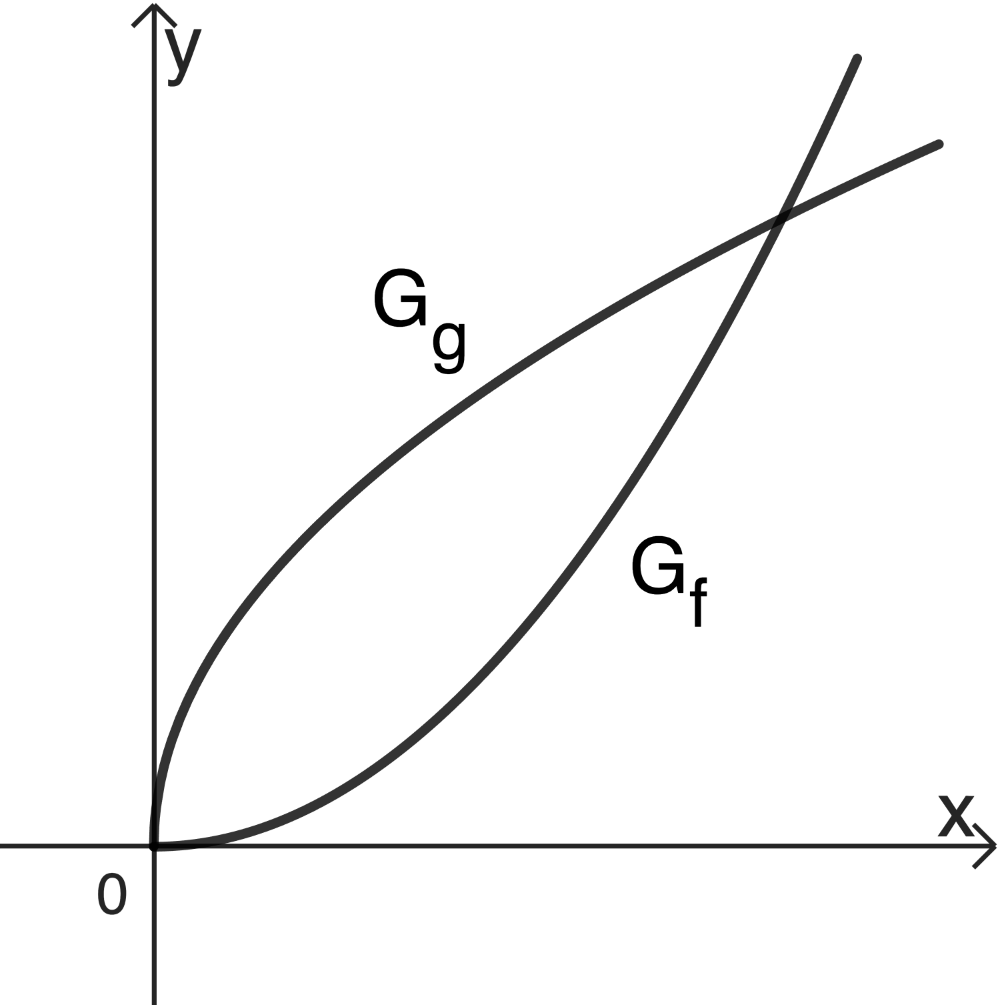
(5 BE)
