mathelike mathelike

Mathematik Beispiel-Abitur Bayern 2026

  • Gegeben ist die in \(\mathbb R\) definierte Funktion \(f \colon x \mapsto \frac{1}{100} \cdot \left( 2x^3 - 43x^2 + 248x \right)\). Abbildung 1 zeigt den Graphen \(G_f\) von \(f\) im Bereich \(0 \leq x \leq 10\).

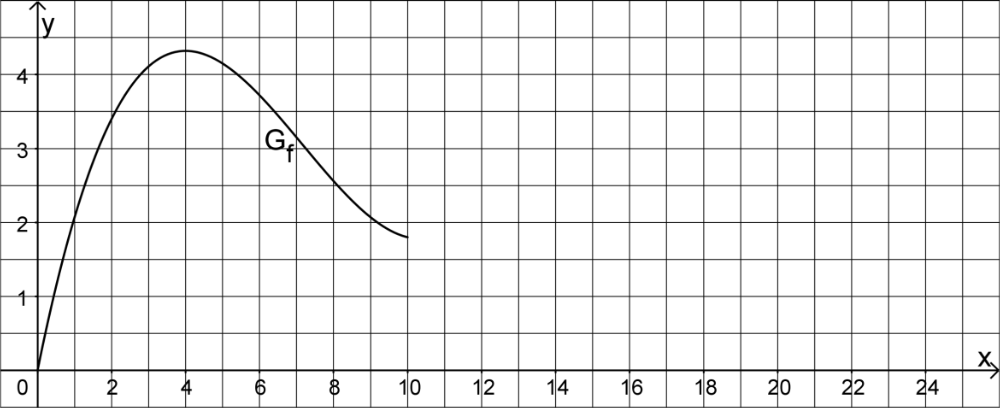    Abbildung 1 Aufgabe B1 Prüfungsteil B Mathematik Beispiel-Abiturprüfung Bayern 2026Abb. 1

    Begründen Sie anhand des Terms von \(f\), dass \(G_f\) nicht symmetrisch bezüglich des Koordinatenursprungs ist, und zeigen Sie rechnerisch, dass \(G_f\) für \(x < 7\frac{1}{6}\) rechtsgekrümmt ist.

    (4 BE) 

  • Die Punkte \(P\) und \(Q\) liegen in der Ebene \(E \colon 5x_1 - 4x_2 + 3x_3 - 6 =-3 0\) und haben voneinander den Abstand 10. Ermitteln Sie mögliche Koordinaten von \(P\) und \(Q\).
    (5 BE)

  • Gegeben sind die Punkte \(A(0|0|0)\), \(B(3|4|1)\), \(C(1|7|3)\), \(D(-2|3|2)\).

    1. Weisen Sie nach, dass das Viereck \(ABCD\) ein Parallelogramm ist.
      (1 BE)
    2. Der Punkt \(T\) liegt auf der Strecke \(\overline{AC}\). Das Dreieck \(ABT\) hat bei \(B\) einen rechten Winkel. Ermitteln Sie das Verhältnis der Länge der Strecke \(\overline{AT}\) zur Länge der Strecke \(\overline{CT}\).
      (4 BE)

  • Eine Gärtnerei, die Tulpen in den Farben Gelb, Orange und Rot züchtet, stellt Sträuße mit jeweils 15 Tulpen zusammen.

    1. Einer der Sträuße soll Tulpen in zwei verschiedenen Farben enthalten. Die Anzahl der Möglichkeiten, diesen Strauß zusammenzustellen, kann mit dem Term \(\displaystyle \binom{3}{2} \cdot 14\) berechnet werden. Beschreiben Sie für jeden der beiden Faktoren die Bedeutung im Sachzusammenhang.
    2. In einem der Sträuße sollen zu jeder der drei Farben mindestens vier und höchstens sechs Tulpen enthalten sein. Bestimmen Sie die Anzahl der Möglichkeiten, diesen Strauß zusammenzustellen.

  • Bei einem Spiel werfen zwei Spieler abwechselnd jeweils drei Würfel. Das Spiel endet, wenn ein Spieler die Augensumme 18 erzielt oder die Augensumme des vorausgegangenen Wurfs des anderen Spielers nicht übertrifft.
    Beim ersten Wurf des Spiels erzielt ein Spieler die Augensumme 15.
    Berechnen Sie die Wahrscheinlichkeit dafür, dass dieser Spieler die Würfel im selben Spiel noch einmal wirft. Erläutern Sie Ihr Vorgehen.
    (5 BE)

  • Der Graph der in \(\mathbb R\) definierten Funktion \(f \colon x \mapsto \frac{1}{4}x^2\) und die Gerade mit der Gleichung \(y = 1\) schließen ein Flächenstück ein (vgl. Abbildung). Durch Rotation diese Flächenstücks um die \(y\)-Achse wird ein Körper erzeugt. Bestimmen Sie das Volumen dieses Körpers.
    (5 BE)

    Abbildung Aufgabe A6 Aufgabengruppe 2 (Wahlteil) Prüfungsteil A Mathematik Beispiel-Abiturprüfung Bayern 2026

  • Gegeben sind die in \(\mathbb R\) definierten Funktionen \(f\) und \(g\). Der Graph von \(f\) ist symmetrisch bezüglich der \(y\)-Achse, der Graph von \(g\) ist symmetrisch bezüglich des Koordinatenursprungs. Beide Graphen haben einen Hochpunkt im Punkt \((2|1)\).

    1. Geben Sie für die Graphen von \(f\) und \(g\) jeweils die Koordinaten und die Art eines weiteren Extrempunkts an.
      (2 BE)
    2. Untersuchen Sie die in \(\mathbb R\) definierte Funktion \(h\) mit \(h(x) = f(x) \cdot \left( g(x) \right)^3\) im Hinblick auf eine mögliche Symmetrie ihres Graphen.
      (3 BE)

  • Die Abbildung zeigt in einem Koordinatensystem modellhaft eine 7 m breite Theaterkulisse, Die linke Seitenwand liegt im Modell in der \(xz\)-Ebene, die rechte Seitenwand ist dazu parallel. Ein auf der Bühne stehender Gegenstand wird von einer Lampe beleuchtet. Die Lampe wird im Modell durch den Punkt \(L(4|0|5)\) dargestellt, die Spitze des Gegenstands durch den Punkt \(S(1|6|2)\).

    Untersuchen Sie rechnerisch, ob der Schatten der Spitze auf der rechten Seitenwand liegt.
    (5 BE)

    Abbildung Aufgabe A4 Aufgabengruppe 1 (Pflichtteil) Prüfungsteil A Mathematik Beispiel-Abiturprüfung Bayern 2026

  • Die Abbildung zeigt den Graphen der Dichtefunktion der normalverteilten Zufallsgröße \(A\).

    Abbildung Aufgabe A3 Aufgabengruppe 1 (Pflichtteil) Prüfungsteil A Mathematik Beispiel-Abiturprüfung Bayern 2026

    1. Die Wahrscheinlichkeit dafür, dass \(A\) einen Wert aus dem Intervall \([6;10]\) annimmt, beträgt etwa 68 %. Berechnen Sie die Wahrscheinlichkeit dafür, dass \(A\) einen Wert annimmt, der größer als 10 ist.
      (2 BE)
    2. Die Zufallsgröße \(B\) ist ebenfalls normalverteilt; der Erwartungswert von \(B\) ist ebenso groß wie der Erwartungswert von \(A\), die Standardabweichung von \(B\) ist größer als die Standarabweichung von \(A\). Skizzieren Sie in der Abbildung einen möglichen Graphen der Dichtefunktion von \(B\).
      (3 BE)

  • Gegeben ist eine in \(\mathbb R\) definierte Funktion \(f\) mit \(f(x) = x^4 - kx^2\), wobei \(k\) eine positive reelle Zahl ist. Die Abbildung zeigt den Graphen von \(f\).

    1. Zeigen Sie, dass \(f'(x) = 2x \cdot \left( 2x^2-k \right)\) ein Term der ersten Ableitungsfunktion von \(f\) ist.
      (1 BE)
    2. Die beiden Tiefpunkte des Graphen von \(f\) haben jeweils die \(y\)-Koordinate \(-1\). Ermitteln Sie den Wert von \(k\).
      (4 BE)

    Abbildung Aufgabe A2 Aufgabengruppe 1 (Pflichtteil) Prüfungsteil A Mathematik Beispiel-Abiturprüfung Bayern 2026

  • Gegeben ist die in \(\mathbb R^+\) definierte Funktion \(f \colon x \mapsto \left( \ln{x} \right)^2\). Der Graph von \(f\) verläuft durch den Punkt \(P(e|1)\).

    1. Die zweite Ableitungsfunktion von \(f\) besitzt an der Stelle \(x = e\) eine Nullstelle mit Vorzeichenwechsel. Geben Sie die Bedeutung dieser Tatsache für den Graphen von \(f\) an.
      (1 BE)
    2. Bestimmen Sie eine Gleichung der Tangente an den Graphen von \(f\) im Punkt \(P\).
      (4 BE)

Seite 3 von 3

mathelike

Mathematik Abiturvorbereitung Bayern

 2025 Christian Rieger・mathelike