Begründen Sie, dass auf der Grundlage von Modell \(A\) die Masse in Kilogramm, um die ein Hund der betrachteten Rasse in den ersten 25 Monaten nach seiner Geburt insgesamt zunimmt, mit dem Term \(\displaystyle \int_0^{10}f(x)dx + 13{,}5\) berechnet werden kann.
(3 BE)
Lösung zu Teilaufgabe 3c
Begründung der Bedeutung des Terms \(\displaystyle \int_0^{10}f(x)dx + 13{,}5\)
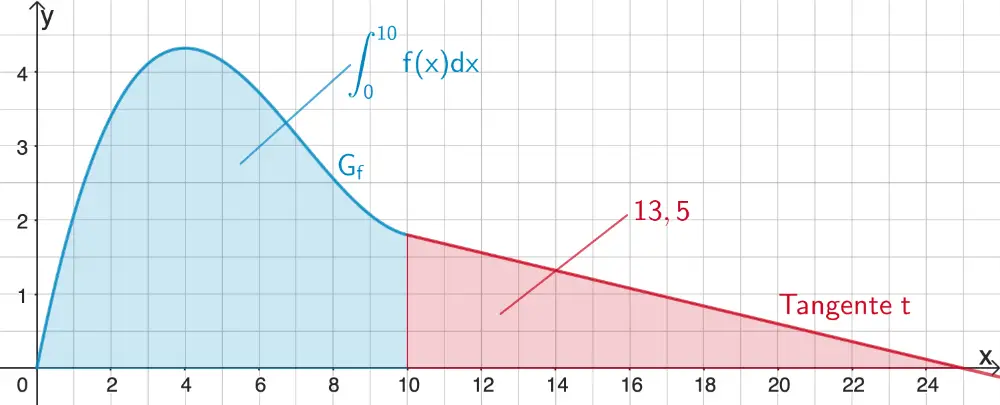
Modell A: Der Graph \(\textcolor{#0087c1}{G_f}\) und die Tangente \(\textcolor{#cc071e}{t}\) beschreiben die momentane Änderungsrate der Körpermasse eines Hundes der betrachteten Rasse in den ersten 25 Monaten nach der Geburt.
Da die Graphen für \(0 < x < 25\) oberhalb der \(x\)-Achse verlaufen, ist die momentane Änderungsrate für \(0 < x < 25\) stets positiv. Das bedeutet, dass die Körpermasse zu jedem Zeitpunkt \(x \in \;]0;25[\) zunimmt.
Anwendung der Integralrechnung
Gesamtänderung einer Größe
Beschreibt eine Funktion \(f\) die momentane Änderungsrate einer Größe in Abhängigkeit von der Zeit \(t\), so errechnet das Integral \(\displaystyle \int_{t_1}^{t_2}f(t)dt\) die Gesamtänderung der Größe im Zeitraum \([t_1;t_2]\).
Die Fläche, die die Graphen mit der \(x\)-Achse einschließen, beschreibt die Gesamtänderung der Körpermasse, das heißt, die Zunahme der Körpermasse in den ersten 25 Monaten nach der Geburt.
Der Inhalt der Fläche, die \(\textcolor{#0087c1}{G_f}\) für \(\textcolor{#0087c1}{0 \leq x \leq 10}\) mit der \(\textcolor{#0087c1}{x}\)-Achse einschließt, lässt sich mithilfe des bestimmten Integrals \(\textcolor{#0087c1}{\displaystyle \int_0^{10}f(x)dx}\) berechnen.
Die Tangente \(\textcolor{#cc071e}{t}\) mit der Gleichung \(\textcolor{#cc071e}{y = -0{,}12x+3}\), die \(x\)-Achse und die Gerade mit der Gleichung \(x = 10\) schließen ein rechtwinkliges Dreieck ein.
\[\begin{align*} &\textcolor{#0087c1}{\displaystyle \int_0^{10}f(x)dx} + \textcolor{#cc071e}{\frac{1}{2} \cdot (25 - 10) \cdot (-0{,}12) \cdot 10 + 3} \\[0.8em] =\, &\textcolor{#0087c1}{\displaystyle \int_0^{10}f(x)dx} + \textcolor{#cc071e}{\frac{1}{2} \cdot 15 \cdot 1{,}8} \\[0.8em] =\, &\textcolor{#0087c1}{\displaystyle \int_0^{10}f(x)dx} + \textcolor{#cc071e}{13{,}5} \end{align*}\]
(Vgl. Mathematik Abiturskript Bayern G9 - 1 Analysis, 1.3.6 Anwendungen der Integralrechnung - Gesamtänderung einer Größe)
