Bei einem Spiel wird ein Würfel einmal geworfen und ein Glücksrad einmal gedreht. Die Seiten des Würfels sind mit den Zahlen von 1 bis 6 durchnummeriert. Das Glücksrad hat zehn gleich große Sektoren, die mit den Zahlen von 1 bis 10 durchnummeriert sind. Man gewinnt das Spiel, wenn die mit dem Glücksrad erzielte Zahl kleiner ist als die mit dem Würfel erzielte Zahl, andernfalls verliert man das Spiel.
Zeigen Sie rechnerisch, dass die Wahrscheinlichkeit dafür, das Spiel zu gewinnen, \(\dfrac{1}{4}\) beträgt.
(3 BE)
Lösung zu Teilaufgabe a
Betrachtung des Spiels als Laplace-Experiment
Das Spiel lässt sich als Laplace-Experiment auffassen. Jede Zahl des Würfels wird mit der Wahrscheinlichkeit \(\frac{1}{6}\) geworfen, und jede Zahl des Glücksrads wird mit der Wahrscheinlichkeit \(\frac{1}{10}\) erzielt (gleich große Sektoren). Sodass insgesamt \(6 \cdot 10 = 60\) gleichwahrscheinliche Ergebnisse möglich sind, deren Wahrscheinlichkeit jeweils \(\frac{1}{60}\) beträgt.
Laplace-Wahrscheinlichkeit eines Ereignisses \(A\)
\[P(A) = \frac{\vert A \vert}{\vert \Omega \vert} = \frac{\text{Anzahl der für} \; A \; \text{günstigen Ergebnisse}}{\text{Anzahl der möglichen Ergebnisse}}\]
Voraussetzung: Alle Ergebnisse (alle Versuchsausgänge) des betrachteten Zufallsexperiments sind gleichwahrscheinlich (Laplace-Experiment).
Anzahl der Ergebnisse des Ereignisses „Gewinn":
„Man gewinnt das Spiel, wenn die mit dem Glücksrad erzielte Zahl kleiner ist als die mit dem Würfel erzielte Zahl, andernfalls verliert man das Spiel."
\[\left.\begin{align*}\text{„Gewinn"} = \{&(\textcolor{#cc071e}{2};\textcolor{#0087c1}{1});\\ &(\textcolor{#cc071e}{3};\textcolor{#0087c1}{1});(\textcolor{#cc071e}{3};\textcolor{#0087c1}{2});\\&(\textcolor{#cc071e}{4};\textcolor{#0087c1}{1});(\textcolor{#cc071e}{4};\textcolor{#0087c1}{2});(\textcolor{#cc071e}{4};\textcolor{#0087c1}{3});\\&(\textcolor{#cc071e}{5};\textcolor{#0087c1}{1});(\textcolor{#cc071e}{5};\textcolor{#0087c1}{2});(\textcolor{#cc071e}{5};\textcolor{#0087c1}{3});(\textcolor{#cc071e}{5};\textcolor{#0087c1}{4});\\&(\textcolor{#cc071e}{6};\textcolor{#0087c1}{1});(\textcolor{#cc071e}{6};\textcolor{#0087c1}{2});(\textcolor{#cc071e}{6};\textcolor{#0087c1}{3});(\textcolor{#cc071e}{6};\textcolor{#0087c1}{4});(\textcolor{#cc071e}{6};\textcolor{#0087c1}{5})\}\end{align*}\; \right\} \; 15\;\text{Ergebnisse}\]
Die Laplace-Wahscheinlichkeit dafür, das Spiel zu gewinnen, beträgt somit:
\[P(\text{„Gewinn"}) = \frac{15}{60} = \frac{1}{4}\]
Betrachtung des Spiels als zweistufiges Zufallsexperiment
Jede Stufe des Spiels (Würfel, Glücksrad) ist für sich betrachtet ein Laplace-Experiment.
| Würfel | Glücksrad | ||
| Zahl | \(P(\text{„}\textcolor{#cc071e}{\text{Zahl}}\text{"})\) | Zahl < Zahl | \(P(\text{„}\textcolor{#0087c1}{\text{Zahl}}<\textcolor{#cc071e}{\text{Zahl}}\text{"})\) |
| \(\textcolor{#cc071e}{2}\) | \(\textcolor{#cc071e}{\dfrac{1}{6}}\) | \(\textcolor{#0087c1}{1}\) | \(\textcolor{#0087c1}{\dfrac{1}{10}}\) |
| \(\textcolor{#cc071e}{3}\) | \(\textcolor{#cc071e}{\dfrac{1}{6}}\) | \(\textcolor{#0087c1}{1;2}\) | \(\textcolor{#0087c1}{\dfrac{2}{10}}\) |
| \(\textcolor{#cc071e}{4}\) | \(\textcolor{#cc071e}{\dfrac{1}{6}}\) | \(\textcolor{#0087c1}{1;2;3}\) | \(\textcolor{#0087c1}{\dfrac{3}{10}}\) |
| \(\textcolor{#cc071e}{5}\) | \(\textcolor{#cc071e}{\dfrac{1}{6}}\) | \(\textcolor{#0087c1}{1;2;3;4}\) | \(\textcolor{#0087c1}{\dfrac{4}{10}}\) |
| \(\textcolor{#cc071e}{6}\) | \(\textcolor{#cc071e}{\dfrac{1}{6}}\) | \(\textcolor{#0087c1}{1;2;3;4;5}\) | \(\textcolor{#0087c1}{\dfrac{5}{10}}\) |
Veranschaulichung als Baumdiagramm:
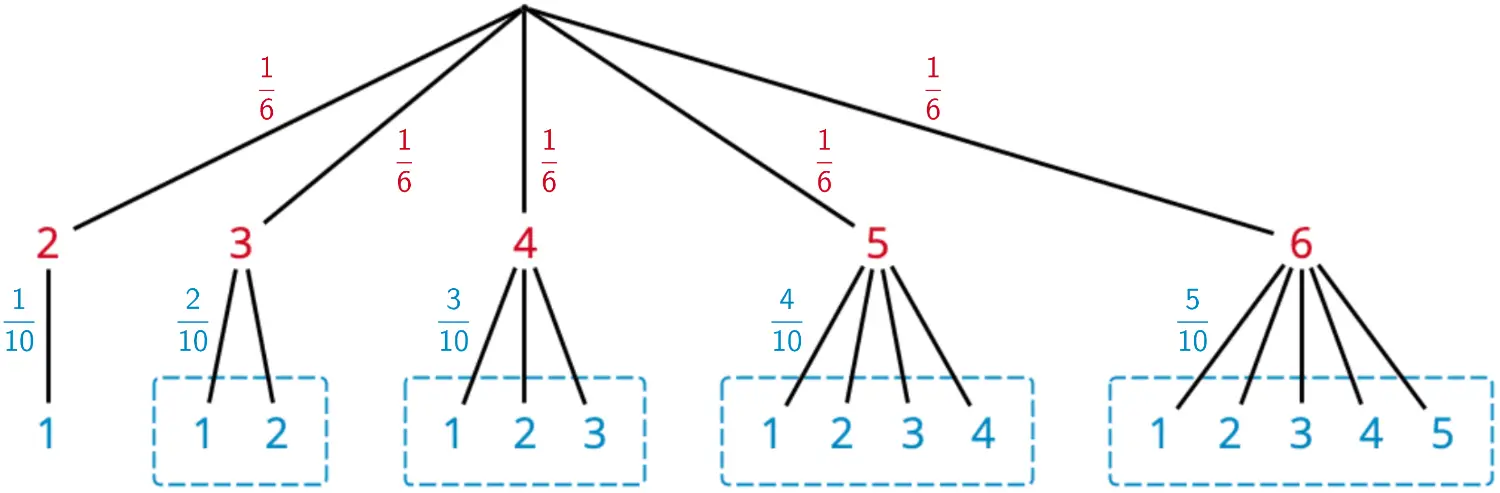
Baumdiagramm der für das Ereignis „Gewinn" relevanten Pfade
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
Mithilfe der 1. und 2. Pfadregel (Produkt- und Summenregel) ergibt sich:
\[\begin{align*}P(\text{„Gewinn"}) &=\underbrace{\underbrace{\textcolor{#cc071e}{\dfrac{1}{6}} \cdot \textcolor{#0087c1}{\dfrac{1}{10}}}_{\text{1. Pfadregel}} + \underbrace{\textcolor{#cc071e}{\dfrac{1}{6}} \cdot \textcolor{#0087c1}{\dfrac{2}{10}}}_{\text{1. Pfadregel}} + \underbrace{\textcolor{#cc071e}{\dfrac{1}{6}} \cdot \textcolor{#0087c1}{\dfrac{3}{10}}}_{\text{1. Pfadregel}} + \underbrace{\textcolor{#cc071e}{\dfrac{1}{6}} \cdot \textcolor{#0087c1}{\dfrac{4}{10}}}_{\text{1. Pfadregel}} + \underbrace{\textcolor{#cc071e}{\dfrac{1}{6}} \cdot \textcolor{#0087c1}{\dfrac{5}{10}}}_{\text{1. Pfadregel}}}_{\text{2. Pfadregel}} \\[0.8em] &= \textcolor{#cc071e}{\dfrac{1}{6}} \cdot \left( \textcolor{#0087c1}{\dfrac{1}{10}} + \textcolor{#0087c1}{\dfrac{2}{10}} + \textcolor{#0087c1}{\dfrac{3}{10}} + \textcolor{#0087c1}{\dfrac{4}{10}} + \textcolor{#0087c1}{\dfrac{5}{10}} \right) \\[0.8em] &=\textcolor{#cc071e}{\dfrac{1}{6}} \cdot \textcolor{#0087c1}{\dfrac{15}{10}} = \frac{15}{60} \\[0.8em] &= \frac{1}{4}\end{align*}\]


