- Details
- Kategorie: Analysis 2
Gegeben ist die in \(\mathbb R\) definierte Funktion \(f\) mit \(f(x) = -\frac{1}{2}x^2+1\).
Zeichnen Sie den Graphen von \(f\) für \(-3 \leq x \leq 3\) in ein Koordinatensystem ein.
(2 BE)
- Details
- Kategorie: Analysis 2
Es gibt genau eine positive reelle Zahl \(a\), für die das Integral \(\displaystyle \int_0^{a} f(x)dx\) den Wert \(0\) hat. Berechnen Sie \(a\).
(3 BE)
- Details
- Kategorie: Analysis 2
Betrachtet wird eine in \(\mathbb R\) definierte ganzrationale Funktion \(g\).
Beschreiben Sie, wie man rechnerisch nachweisen kann, dass \(2\) eine Wendestelle von \(g\) ist.
(2 BE)
- Details
- Kategorie: Analysis 2
Der Punkt \((2|3)\) ist der einzige Wendepunkt des Graphen von \(g\). Die in \(\mathbb R\) definierte Funktion \(h\) ist gegeben durch \(h(x) = g(2x) - 1\).
Geben Sie die Koordinaten des Wendepunkts des Graphen von \(h\) an und begründen Sie Ihre Angabe.
(3 BE)
- Details
- Kategorie: Analysis 2
Gegeben ist die in \(\mathbb R\) definierte Funktion \(f\) mit \(f(x) = \frac{1}{4}x^3-3x\).
Für die zweite Ableitungsfunktion von \(f\) gilt \(f''(2) \neq 0\). Zeigen Sie, dass \(2\) eine Extremstelle von \(f\) ist.
(2 BE)
- Details
- Kategorie: Analysis 2
Einer der Graphen I und II in Abbildung 1 ist der Graph einer Stammfunktion von \(f\). Geben Sie diesen Graphen an und begründen Sie Ihre Angabe.
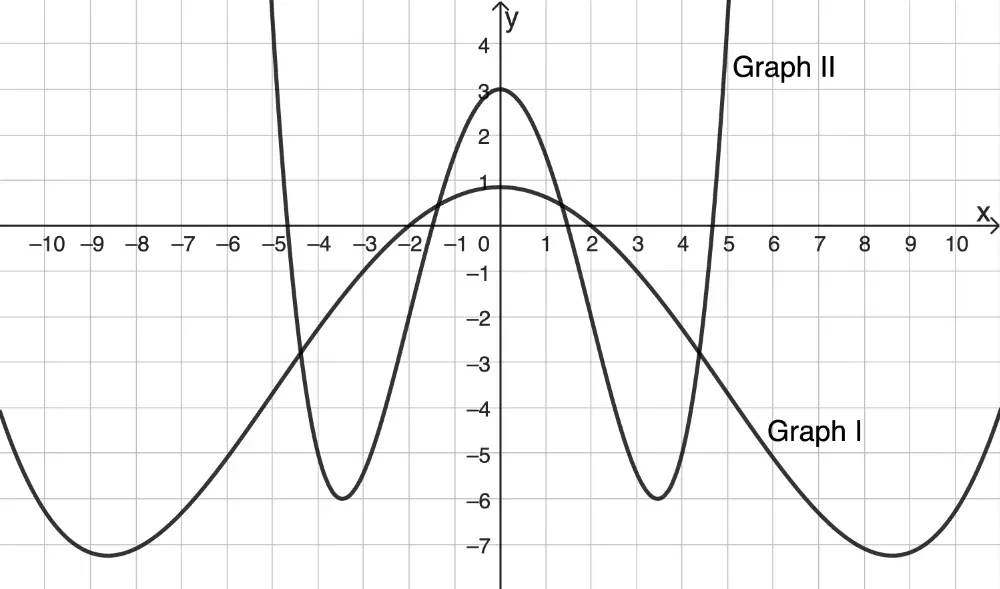Abb. 1
(3 BE)
- Details
- Kategorie: Analysis 2
Gegeben ist die Funktion \(g \colon x \mapsto \sqrt{x-2}\) mit \(x \in [2;+\infty[\). Abbildung 2 zeigt den Graphen \(G\) von \(g\) sowie den Punkt \(P(3|1)\). Die Gerade mit der Gleichung \(y = \frac{1}{2}x-\frac{1}{2}\) ist Tangente an \(G\) im Punkt \(P\) und hat mit \(G\) nur den Punkt \(P\) gemeinsam.
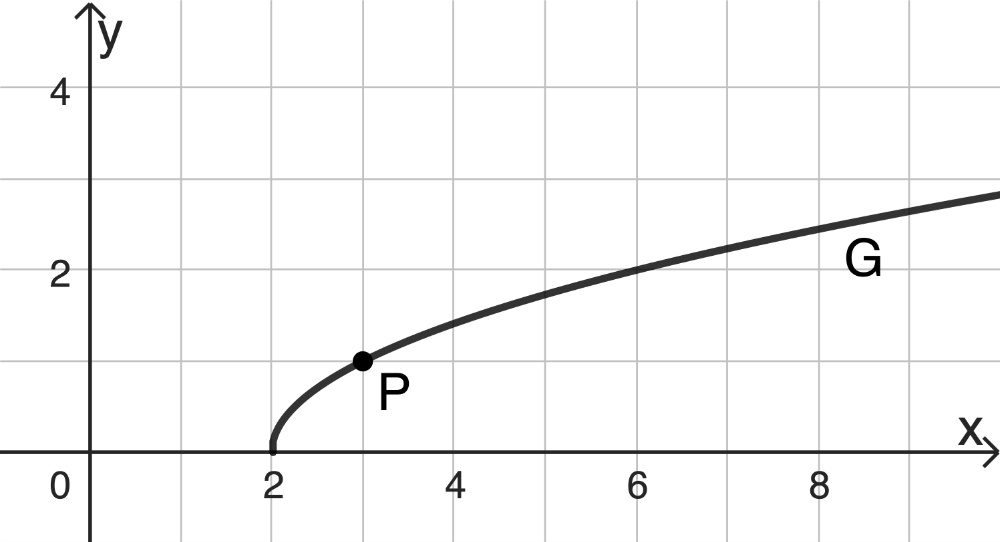Abb. 2
Zeichnen Sie die Tangente in Abbildung 2 ein.
(1 BE)
- Details
- Kategorie: Analysis 2
Betrachtet wird eine Gerade, die mit \(G\) sowohl den Punkt \(P\) als auch einen weiteren Punkt gemeinsam hat. Geben Sie alle möglichen Steigungen dieser Gerade an.
(4 BE)
