- Details
- Kategorie: Analysis 2
Gegeben ist die in \(\mathbb R\) definierte Funktion \(f \colon x \mapsto 5x \cdot e^{-x}\). Abbildung 1 zeigt den Graphen \(G\) von \(f\).
\(G\) hat genau einen Extrempunkt. Berechnen Sie die Koordinaten des Extrempunkts von \(G\).
(zur Kontrolle: \(\big(1|\frac{5}{e}\big)\))
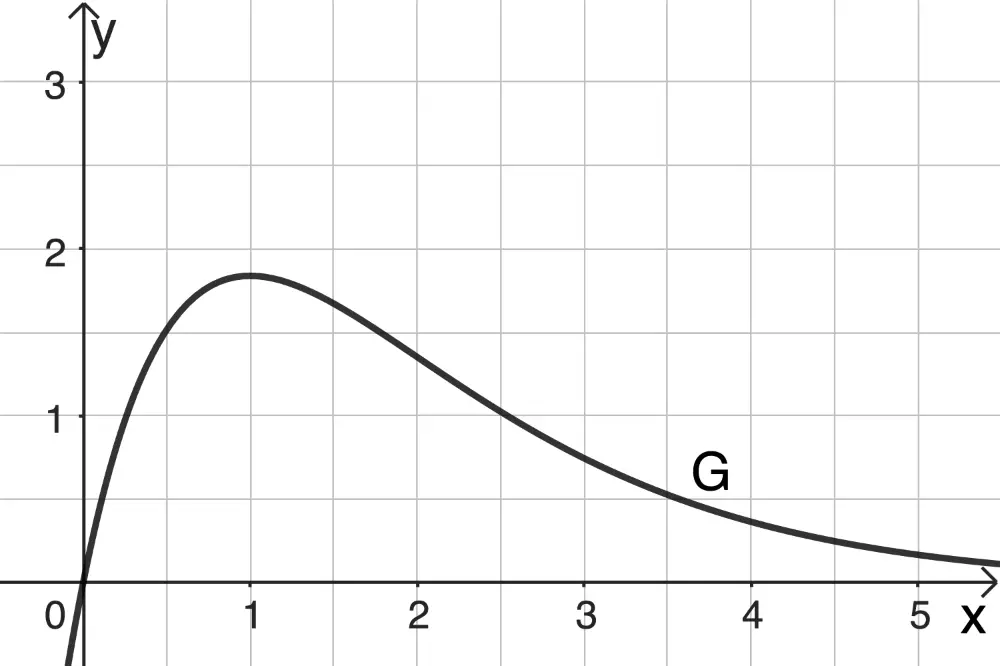Abb. 1
(4 BE)
- Details
- Kategorie: Analysis 2
Die Tangente \(t\) an \(G\) in dessen Wendepunkt hat die Gleichung \(y = -\dfrac{5}{e^2}x + \dfrac{20}{e^2}\). Ermitteln Sie eine Gleichung der Gerade, die den Extrempunkt von \(G\) enthält und senkrecht zu \(t\) verläuft.
(3 BE)
- Details
- Kategorie: Analysis 2
Betrachtet wird die in \([1;+\infty[\) definierte Funktion \(h\) mit \(h(x) = f(x)\).
Begründen Sie, dass die Funktion \(f\) nicht umkehrbar, die Funktion \(h\) jedoch umkehrbar ist. Geben Sie den Definitions- und Wertebereich der Umkehrfunktion von \(h\) an.
(6 BE)
- Details
- Kategorie: Analysis 2
Abbildung 2 zeigt eine Figur, die modellhaft das Wappen eines Sportvereins beschreibt. Die Begrenzungslinien der Figur werden durch einen Teil der Gerade mit der Gleichung \(y = 5\) sowie durch die Kurvenstücke \(H_1\) und \(H_2\) beschrieben:
- \(H_1\) entsteht, indem \(G\) für \(x \in [\ln{5};5]\) an der Gerade mit der Gleichung \(y = x\) gespiegelt wird.
- \(H_2\) entsteht durch Spiegeln von \(H_1\) an der Gerade mit der Gleichung \(x = \ln{5}\).
Abb. 2
Der Punkt \(S(\ln{5}|\ln{5})\) ist gemeinsamer Punkt von \(H_1\) und \(H_2\).
Begründen Sie, dass mit dem Term \(\displaystyle 2 \cdot \left( (5 - \ln{5}) \cdot \ln{5} - \int_{\ln{5}}^5 f(x)dx\right)\) der Flächeninhalt der Figur berechnet werden kann.
(5 BE)
- Details
- Kategorie: Analysis 2
Die in \(\mathbb R\) definierte Funktion \(F \colon x \mapsto -5(x+1)\cdot e^{-x}\) ist eine Stammfunktion von \(f\). Berechnen Sie mit dem Term aus Aufgabe 1d den Flächeninhalt der Figur auf eine Nachkommastelle genau.
(3 BE)
- Details
- Kategorie: Analysis 2
Betrachtet wird die Schar der in \(\mathbb R\) definierten Funktionen \(g_k \colon x \mapsto -5x \cdot e^{-kx}\) mit \(k \in \mathbb R \backslash \{0\}\). Abbildung 3 zeigt vier Graphen der Schar, die zu den Werten \(k = -1\), \(k = -0{,}5\), \(k = 0{,}5\) und \(k = 1\) gehören.
Der Graph III kann durch Spiegeln von \(G\) (vgl. Abbildung 1) an der \(x\)-Achse erzeugt werden. Geben Sie den zugehörigen Wert von \(k\) sowie die Koordinaten des Tiefpunkts von Graph III an. Ordnen Sie den drei übrigen Werten von \(k\) den jeweils passenden Graphen zu.
Abb. 3
(5 BE)
- Details
- Kategorie: Analysis 2
Zeigen Sie, dass \(g_k(-x) = -g_{-k}(x)\) für alle \(x \in \mathbb R\) gilt, und interpretieren Sie diese Gleichung mit Blick auf die Graphen der Funktionen \(g_k\) und \(g_{-k}\).
(4 BE)
