- Details
- Kategorie: Geometrie 2
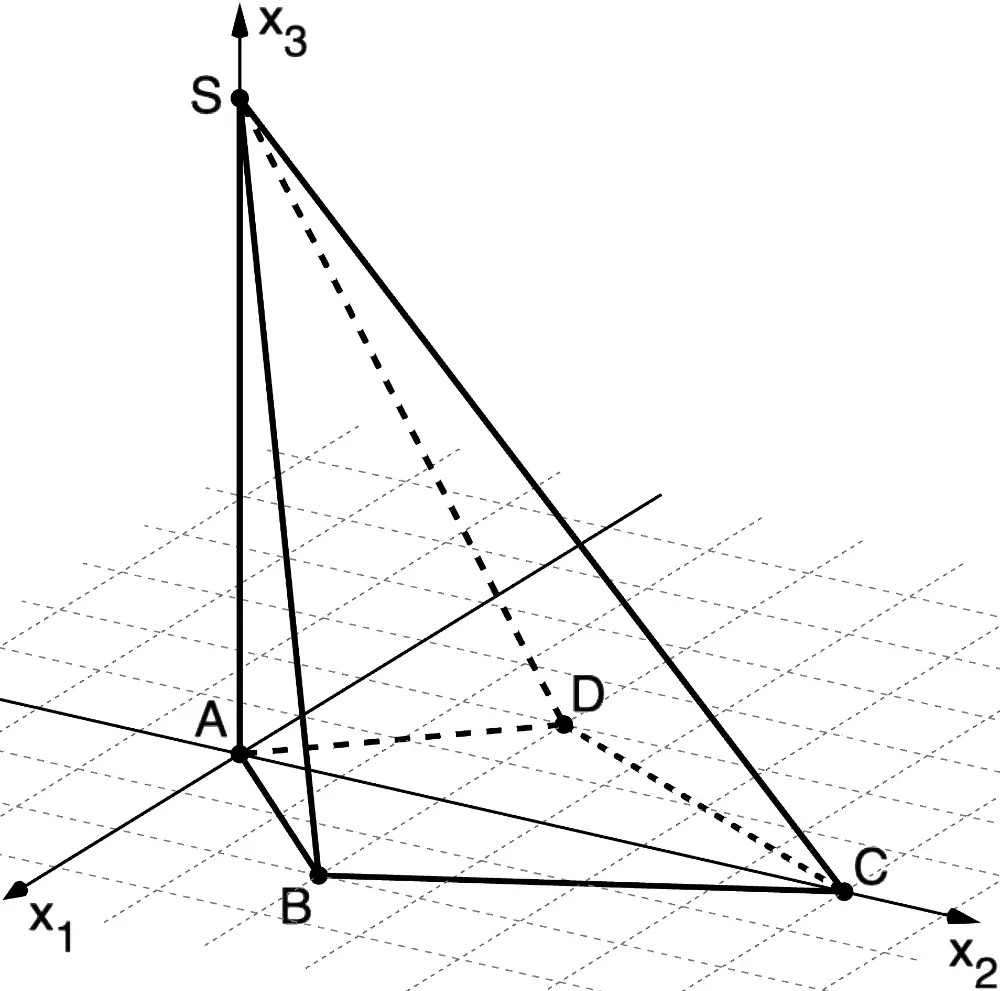
Die Abbildung zeigt die Pyramide \(ABCDS\). Ihre Grundfläche \(ABCD\) ist ein Drachenviereck mit den Eckpunkten \(A(0|0|0)\), \(B(2|2|0)\), \(C(0|6|0)\) und \(D(-2|2|0)\). Der Punkt \(S(0|0|6)\) ist die Spitze der Pyramide.
Berechnen Sie die kleinste Kantenlänge sowie das Volumen der Pyramide \(ABCDS\).
(4 BE)
- Details
- Kategorie: Geometrie 2
Die Seitenfläche \(BCS\) der Pyramide liegt in der Ebene \(E\).
Betrachtet werden die Vektoren \(\overrightarrow{n}\), deren Koordinaten nicht alle gleich null sind. Begründen Sie, dass folgende Aussage richtig ist:
Gilt für einen solchen Vektor \(\overrightarrow{n} \circ \begin{pmatrix} -1\\2\\0 \end{pmatrix}= 0\) und \(\overrightarrow{n} \circ \begin{pmatrix} -1\\-1\\3 \end{pmatrix} = 0\), so ist er ein Normalenvektor von \(E\).
(3 BE)
- Details
- Kategorie: Geometrie 2
Die Ebene \(E\) hat die Gleichung \(2x_1 + x_2 + x_3 = 6\). Bestimmen Sie die Größe des Winkels, den \(E\) mit der \(x_1x_2\)-Ebene einschließt.
(3 BE)
- Details
- Kategorie: Geometrie 2
Gegeben ist die Schar der Ebenen \(F_k \colon k \cdot x_2 + (k-2) \cdot x_3 = 2k\) mit \(k \in \; ]0;3[\). Jede Ebene \(F_k\) der Schar schneidet die Pyramide \(ABCDS\) in einem Dreieck \(BDQ_k\), wobei der Punkt \(Q_k\) auf der Strecke \([SC]\) liegt.
Geben Sie eine Gleichung der Ebene \(F_2\) an und zeichnen Sie in die Abbildung die Schnittfigur von \(F_2\) mit der Pyramide \(ABCDS\) ein.
(4 BE)
- Details
- Kategorie: Geometrie 2
Es gibt einen Wert von \(k\), für den der Flächeninhalt des Dreiecks \(BDQ_k\) minimal ist. Ermitteln Sie diesen Wert.
(6 BE)


