Abiturlösungen Mathematik Bayern 2025 Prüfungsteil B Stochastik 2

Unter den Touristen eines Naturparks nutzen erfahrungsgemäß 15 % das Fahrrad für Ausflüge vor Ort. Im Folgenden werden diese Touristen als Radausflügler bezeichnet. Es soll davon ausgegangen werden, dass in einer zufälligen Auswahl von Touristen des Naturparks die Anzahl der Radausflügler binomialverteilt ist.

Für eine Stichprobe werden 50 Touristen des Naturparks zufällig ausgewählt.

Bestimmen Sie die Wahrscheinlichkeit dafür, dass sich in der Stichprobe genau fünf Radausflügler befinden.

(1 BE)

Ermitteln Sie die Wahrscheinlichkeit dafür, dass die Anzahl der Radausflügler in der Stichprobe um mindestens 10 % größer ist als der Erwartungswert für diese Anzahl.

(3 BE)

Um den Naturpark als Reiseziel attraktiver zu machen, setzt der dortige Tourismusverband Shuttlebusse ein. Die Fahrkarten für diese Busse können ausschließlich online gebucht werden und sind jeweils für einen bestimmten Tag gültig. Erfahrungsgemäß werden 80 % aller gebuchten Fahrkarten spätestens am Vortag der Fahrt gebucht. Von diesen spätestens am Vortag gebuchten Fahrkarten werden 90 % auch tatsächlich genutzt. Bei den restlichen, erst am Tag der Fahrt gebuchten Fahrkarten liegt dieser Anteil mit 95 % etwas höher.

Stellen Sie den Sachverhalt in einem beschrifteten Baumdiagramm dar.

(3 BE)

Betrachtet wird eine zufällig ausgewählte, nicht genutzte Fahrkarte. Beurteilen Sie die folgende Aussage:

Die Wahrscheinlichkeit dafür, dass diese Fahrkarte spätestens am Vortag gebucht wurde, ist achtmal so groß wie die Wahrscheinlichkeit dafür, dass sie erst am Tag der Fahrt gebucht wurde.

(3 BE)

Der Tourismusverband vermutet, dass sich der bisherige Anteil der Radausflügler unter den Touristen von 15 % durch den Einsatz der Shuttlebusse erhöht hat. Die Verantwortlichen planen die Durchführung eines Signifikanztests mit einem Signifikanzniveau von 8 % und der Nullhypothese „Der Anteil der Radausflügler unter allen Touristen liegt bei höchstens 15 %." Vor der Durchführung des Tests wird festgelegt, die Shuttlebusses nur dann weiterzubetreiben, wenn die Nullhypothese aufgrund des Testergebnisses abgelehnt wird.

Es ist geplant, den Test auf der Grundlage einer Stichprobe von 200 Touristen durchzuführen. Bestimmen Sie die zugehörige Entscheidungsregel.

(5 BE)

Angenommen, der beschriebene Test wird auf der Grundlage einer Stichprobe von nur 100 Touristen durchgeführt. In diesem Fall wird die Nullhypothese abgelehnt, wenn sich unter diesen mehr als 20 Radausflügler befinden. Damit die Wahrscheinlichkeit für den Fehler zweiter Art höchstens 30 % beträgt, muss der tatsächliche Anteil der Radausflügler unter allen Touristen mindestens einen bestimmten Wert haben. Ermitteln Sie diesen Wert auf ganze Prozent genau und beschreiben Sie die Bedeutung des Fehlers zweiter Art im Sachzusammenhang.
Hinweis: Die unten abgebildete Tabelle ergänzt das zugelassene Tafelwerk.

Binomialverteilung kumulativ; \(k \mapsto \sum \limits_{i\,=\,0}^k B(n;p;i)\)

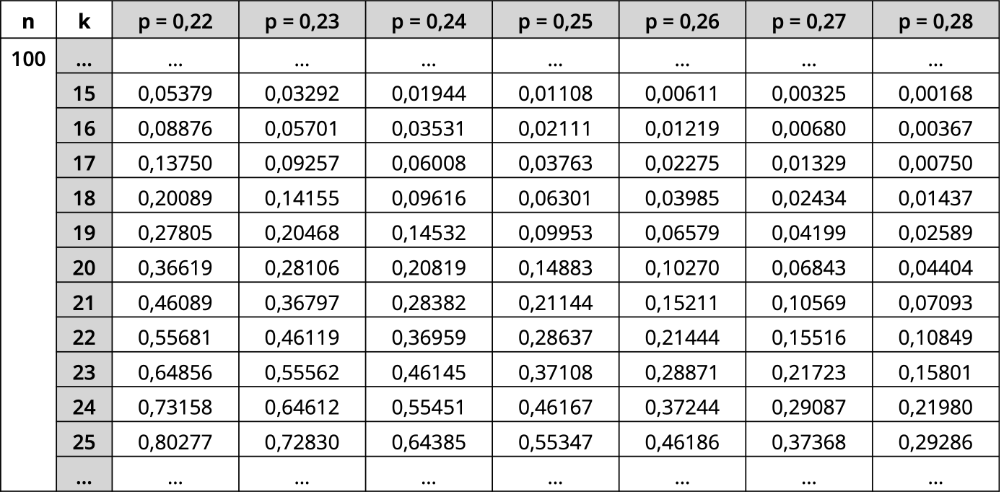
(5 BE)